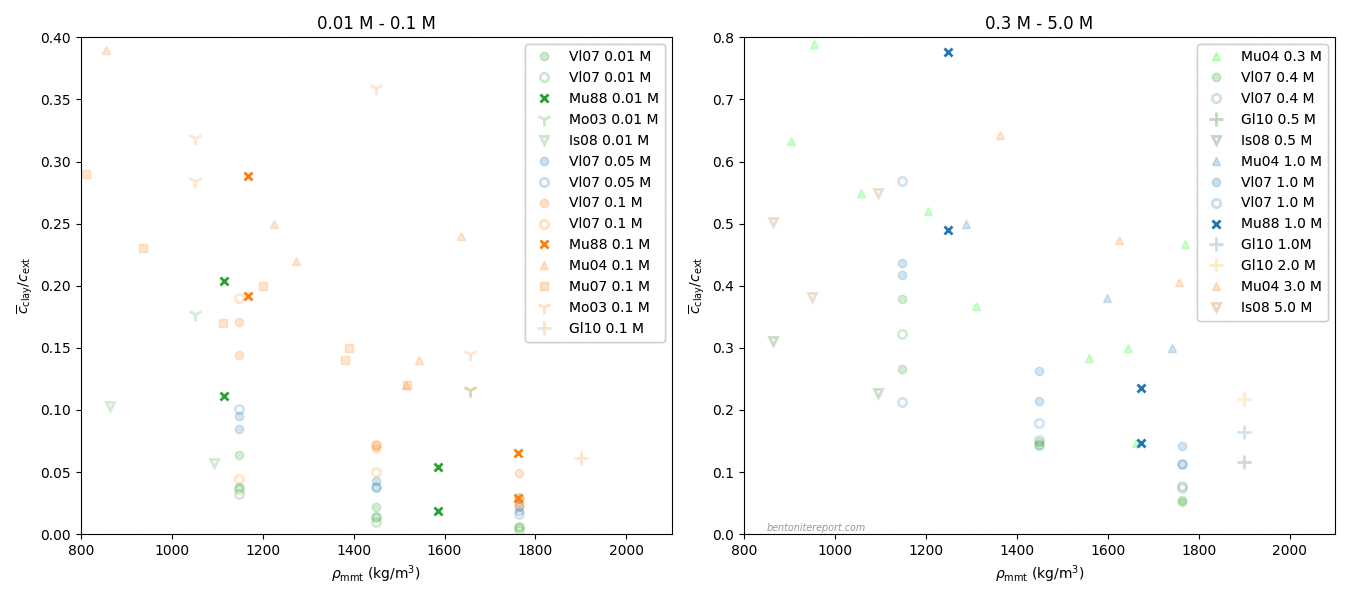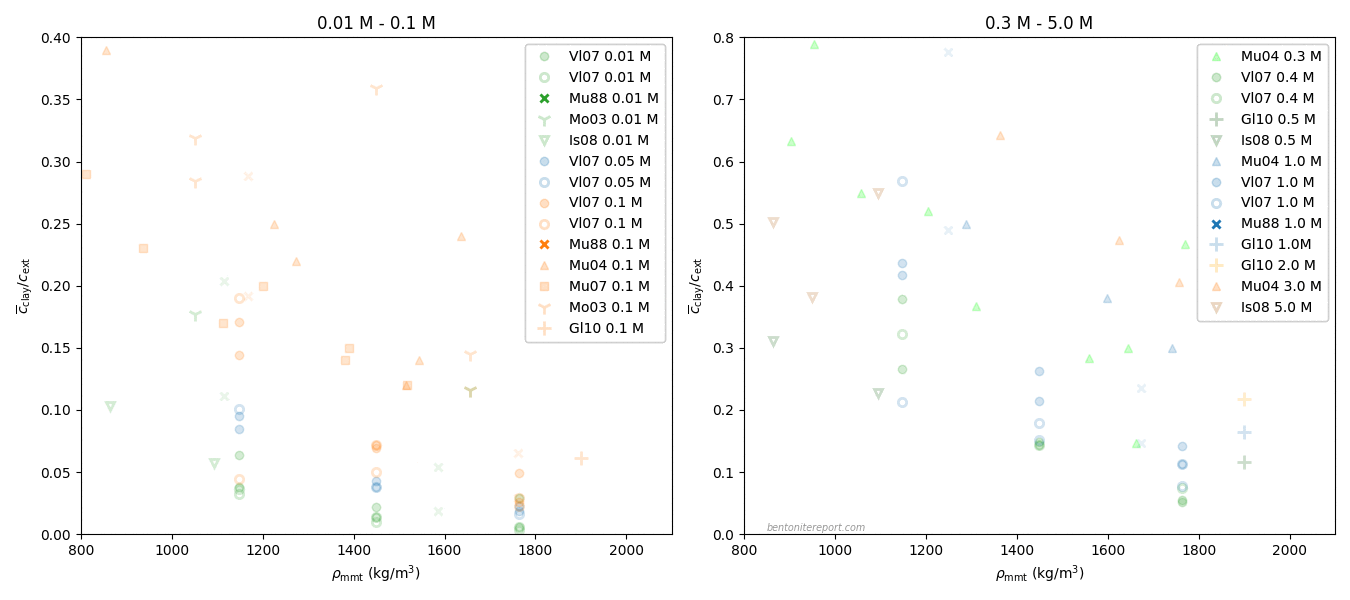
In the ongoing assessment of chloride equilibrium concentrations in bentonite, we here take a closer look at the study by Van Loon et al. (2007), in the following referred to as Vl07. We thus assess the 54 points indicated here (click on figures to enlarge)

Vl07 is centered around a set of through-diffusion tests in “KWK” bentonite samples of nominal dry densities 1.3 g/cm³, 1.6 g/cm³, and 1.9 g/cm³. For each density, chloride tracer diffusion tests were conducted with NaCl background concentrations 0.01 M, 0.05 M, 0.1 M, 0.4 M, and 1.0 M. In total, 15 samples were tested. The samples are cylindrical with diameter 2.54 cm and height 1 cm, giving an approximate volume of 5 cm³. We refer to a specific test or sample using the nomenclature “nominal density/external concentration”, e.g. the sample of density 1.6 g/cm³ contacted with 0.1 M is labeled “1.6/0.1”.

After maintaining steady-state, the external solutions were replaced with tracer-free solutions (with the same background concentration), and tracers in the samples were allowed to diffuse out. In this way, the total tracer amount in the samples at steady-state was estimated. For tests with background concentrations 0.01 M, 0.1 M, and 1.0 M, the outflux was monitored in some detail, giving more information on the diffusion process. After finalizing the tests, the samples were sectioned and analyzed for stable (non-tracer) chloride. In summary, the tests were performed in the following sequence

1. Saturation stage
   
2. Through-diffusion stage
   • Transient phase
     
   • Steady-state phase
     
3. Out-diffusion stage
   
4. Sectioning
   

Uncertainty of samples

The used bentonite material is referred to as “Volclay KWK”. Similar to “MX-80”, “KWK” is just a brand name (it seems to be used mainly in wine and juice production). In contrast to “MX-80”, “KWK” has been used in only a few research studies related to radioactive waste storage. Of the studies I’m aware, only Vejsada et al. (2006) provide some information relevant here.¹

Vl07 state that “KWK” is similar to “MX-80” and present a table with chemical composition and exchangeable cation population of the bulk material. As the chemical composition in this table is identical to what is found in various “technical data sheets”, we conclude that it does not refer to independent measurements on the actual material used (but no references are provided). I have not been able to track down an exact origin of the stated exchangeable cation population, but the article gives no indication that these are original measurements (and gives no reference). I have found a specification of “Volclay bentonite” in this report from 1978(!) that states similar numbers (this document also confirms that “MX-80” and “KWK” are supposed to be the same type of material, the main difference being grain size distribution). We assume that exchangeable cations have not been determined explicitly for the material used in Vl07.

In a second table, Vl07 present a mineral composition of “KWK”, which I assume has been determined as part of the study. But this is not fully clear, as the only comment in the text is that the composition was “determined by XRD-analysis”. The impression I get from the short material description in Vl07 is that they rely on that the material is basically the same as “MX-80” (whatever that is).

Montmorillonite content

Vl07 state a smectite content of about 70%. Vejsada et al. (2006), on the other hand, state a smectite content of 90%, which is also stated in the 1978 specification of “Volclay bentonite”. Note that 70% is lower and 90% is higher than any reported montmorillonite content in “MX-80”. Regardless whether or not Vl07 themselves determined the mineral content, I’d say that the lack of information here must be considered when estimating an uncertainty on the amount of montmorillonite (“smectite”) in the used material. If we also consider the claim that “KWK” is similar to “MX-80”, which has a documented montmorillonite content in the range 75 — 85%, an uncertainty range for “KWK” of 70 — 90% is perhaps “reasonable”.

Cation population

Vl07 state that the amount exchangeable sodium is in the range 0.60 — 0.65 eq/kg, calcium is in the range 0.1 — 0.3 eq/kg, and magnesium is in the range 0.05 — 0.2 eq/kg. They also state a cation exchange capacity in the range 0.76 — 1.2 eq/kg, which seems to have been obtained from just summing the lower and upper limits, respectively, for each individual cation. If the material is supposed to be similar to “MX-80”, however, it should have a cation exchange capacity in the lower regions of this range. Also, Vejsada et al. (2006) state a cation exchange capacity of 0.81 eq/kg. We therefore assume a cation exchange capacity in the range 0.76 — 0.81, with at least 20% exchangeable divalent ions.

Soluble accessory minerals

According to Vl07, “KWK” contains substantial amounts of accessory carbonate minerals (mainly calcite), and Vejsada et al. (2006) also state that the material contains calcite. The large spread in calcium and magnesium content reported for exchangeable cations can furthermore be interpreted as an artifact due to dissolving calcium- and magnesium minerals during the measurement of exchangeable cations (but we have no information on this measurement). Vl07 and Vejsada et al. (2006) do not state any presence of gypsum, which otherwise is well documented in “MX-80”. I do not take this as evidence for “KWK” being gypsum free, but rather as an indication of the uncertainty of the composition (the 1978 specification mentions gypsum).

Sample density

Vl07 don’t report measured sample densities (the samples are ultimately sectioned into small pieces), but estimate density from the water uptake in the saturation stage. The reported average porosity intervals are 0.504 — 0.544 for the 1.3 g/cm³ samples, 0.380 — 0.426 for the 1.6 g/cm³ samples, and 0.281 — 0.321 for the 1.9 g/cm³ samples. Combining these values with the estimated interval for montmorillonite content, we can derive an interval for the effective montmorillonite dry density by combining extreme values. The result is (assuming grain density 2.8 g/cm³, adopted in Vl07).

Sample density (g/cm3)	EMDD interval (g/cm3)
1.3	1.04 — 1.32
1.6	1.36 — 1.67
1.9	1.67 — 1.95

These intervals must not be taken as quantitative estimates, but as giving an idea of the uncertainty.

Uncertainty of external solutions

Samples were water saturated by first contacting them from one side with the appropriate background solution (NaCl). From the picture in the article, we assume that this solution volume is 200 ml. After about one month, the samples were contacted with a second NaCl solution of the same concentration, and the saturation stage was continued for another month. The volume of this second solution is harder to guess: the figure shows a smaller container, while the text in the figure says “200 ml”. The figure shows the set-up during the through-diffusion stage, and it may be that the containers used in the saturation stage not at all correspond to this picture. Anyway, to make some sort of analysis we will assume the two cases that samples were contacted with solutions of either volume 200 ml, or 400 ml (200 ml + 200 ml) during saturation.

The through-diffusion tests were started by replacing the two saturating solutions: on the left side (the source) was placed a new 200 ml NaCl solution, this time spiked with an appropriate amount of ³⁶Cl tracers, and on the right side (the target) was placed a fresh, tracer free NaCl solution of volume 20 ml. The through-diffusion tests appear to have been conducted for about 55 days. During this time, the target solution was frequently replaced in order to keep it at a low tracer concentration. The source solution was not replaced during the through-diffusion test.

As (initially) pure NaCl solutions are contacted with bentonite that contains significant amounts of calcium and magnesium, ion exchange processes are inevitably initiated. Thus, in similarity with some of the earlier assessed studies, we don’t have full information on the cation population during the diffusion stages. As before, we can simulate the process to get an idea of this ion population. In the simulation we assume a bentonite containing only sodium and calcium, with an initial equivalent fraction of calcium of 0.25 (i.e. sodium fraction 0.75). We assume sample volume 5 cm³, cation exchange capacity 0.785 eq/kg, and Ca/Na selectivity coefficient 5.

Below is shown the result of equilibrating an external solution of either 200 or 400 ml with a sample of density 1.6 cm³/g, and the corresponding result for density 1.3 cm³/g and external volume 400 ml. As a final case is also displayed the result of first equilibrating the sample with a 400 ml solution, and then replacing it with a fresh 200 ml solution (as is the procedure when the through-diffusion test is started).

Although the results show some spread, these simulations make it relatively clear that the ion population in tests with the lowest background concentration (0.01 M) probably has not changed much from the initial state. In tests with the highest background concentration (1.0 M), on the other hand, significant exchange is expected, and the material is consequently transformed to a more pure sodium bentonite. In fact, the simulations suggest that the mono/divalent cation ratio is significantly different in all tests with different background concentrations.

Note that the simulations do not consider possible dissolution of accessory minerals and therefore may underestimate the amount divalent ions still left in the samples. We saw, for example, that the material used in Muurinen et al. (2004) still contained some calcium and magnesium although efforts were made to convert it to pure sodium form. Note also that the present analysis implies that the mono/divalent cation ratio probably varies somewhat in each individual sample during the course of the diffusion tests.

Direct measurement of clay concentrations

Chloride clay concentration profiles were measured in all samples after finishing the diffusion tests, by dispersing sample sections in deionized water. Unfortunately, Vl07 only present this chloride inventory in terms of “effective” or “Cl-accessible porosity”, a concept often encountered in evaluation of diffusivity. However, “effective porosity” is not what is measured, but is rather an interpretation of the evaluated amount of chloride in terms of a certain pore volume fraction. Vl07 explicitly define effective porosity as \(V_\mathrm{Cl}/V_\mathrm{1g}\), where \(V_\mathrm{1g}\) is the “volume of a unit mass of wet bentonite”, and \(V_\mathrm{Cl}\) is the “volume of the Cl-accessible pores of a unit mass of bentonite”. While \(V_\mathrm{1g}\) is accessible experimentally, \(V_\mathrm{Cl}\) is not. Vl07 further “derive” a formula for the effective porosity (called \(\epsilon_\mathrm{eff}\) hereafter)

\begin{equation} \epsilon_\mathrm{eff} = \frac{n’_\mathrm{Cl}\cdot \rho_\mathrm{Rf}}{C_\mathrm{bkg}} \tag{1} \end{equation}

where \(n’_\mathrm{Cl}\) is the amount chloride per mass bentonite, \(\rho_\mathrm{Rf}\) is the density of the “wet” bentonite, and \(C_\mathrm{bkg}\) is the background NaCl concentration.² In contrast to \(V_\mathrm{Cl},\) these three quantities are all accessible experimentally, and the concentration \(n’_\mathrm{Cl}\) is what has actually been measured. For a result independent of how chloride is assumed distributed within the bentonite, we thus multiply the reported values of \(\epsilon_\mathrm{eff}\) by \(C_\mathrm{bkg}\), which basically gives the (experimentally accessible) clay concentration

\begin{equation} \bar{C} = \frac{\epsilon_\mathrm{eff} \cdot C_\mathrm{bkg}}{\phi} \tag{2} \end{equation}

Here we also have divided by sample porosity, \(\phi\), to relate the clay concentration to water volume rather than total sample volume. Note that eq. 2 is not derived from more fundamental quantities, but allows for “de-deriving” a quantity more directly related to measurements. (I.e., what is reported as an accessible volume is actually a measure of the clay concentration.)

It is, however, impossible (as far as I see) to back-calculate the actual value of \(n’_ \mathrm{Cl}\) from provided formulas and values of \(\epsilon_\mathrm{eff}\), because masses and volumes of the sample sections are not provided. Therefore, we cannot independently assess the procedure used to evaluate \(\epsilon_\mathrm{eff}\), and simply have to assume that it is adequate.³ Here are the reported values of \(\epsilon_\mathrm{eff}\) for each test, and the corresponding evaluation of \(\bar{C}\) using eq. 2 (column 3)

Test	\(\epsilon_\mathrm{eff}\) (reported)	\(\bar{C}/C_\mathrm{bkg}\) (from \(\epsilon_\mathrm{eff}\))	\(\bar{C}/C_\mathrm{bkg}\) (re-evaluated)
1.3/0.01	0.034	0.06	0.051
1.3/0.05	0.045	0.08	–
1.3/0.1	0.090*	0.17	0.162
1.3/0.4	0.140	0.26	–
1.3/1.0	0.220	0.41	0.400
1.6/0.01	0.009	0.02	0.019
1.6/0.05	0.016**	0.04	–
1.6/0.1	0.029	0.07	0.066
1.6/0.4	0.060	0.14	–
1.6/1.0	0.110	0.26	0.239
1.9/0.01	0.009	0.03	discarded
1.9/0.05	0.007	0.02	–
1.9/0.1	0.015	0.05	0.044
1.9/0.4	0.017	0.05	–
1.9/1.0	0.044	0.14	0.128

When using eq. 2 we have adopted porosities 0.536, 0.429, and 0.322, respectively, for densities 1.3 g/cm³, 1.6 g/cm³, and 1.9 g/cm³.

The tabulated \(\epsilon_\mathrm{eff}\) values are evaluated as averages of the clay concentration profiles (presented as effective porosity profiles), which look like this for the samples exposed to background concentrations 0.01 M, 0.1 M and 1.0 M (profiles for 0.05 M and 0.4 M are not presented in Vl07)

The chloride concentration increases near the interfaces in all samples; we have discussed this interface excess effect in previous posts. Vl07 deal with this issue by evaluating the averages only for the inner parts of the samples. I performed a similar evaluation, also presented in the above figures (blue lines). In this evaluation I adopted the criterion to exclude all points situated less than 2 mm from the interfaces (Vl07 seem to have chosen points a bit differently). The clay concentration reevaluated in this way is also listed in the above table (last column). Given that I have only used nominal density for each sample (I don’t have information on the actual density of the sample sections), I’d say that the re-evaluated values agree well with those de-derived from reported \(\epsilon_\mathrm{eff}\). One exception is the sample 1.9/0.01, which is seen to have concentration points all over the place (or maybe detection limit is reached?). While Vl07 choose the lowest three points in their evaluation, here we choose to discard this result altogether. I mean that it is rather clear that this concentration profile cannot be considered to represent equilibrium.

As the reevaluation gives similar values as those reported, and since we lack information for a full analysis, we will use the values de-derived from reported \(\epsilon_\mathrm{eff}\) in the continued assessment (except for sample 1.9/0.01).

Diffusion related estimations

Vl07 determine diffusion parameters by fitting various mathematical expressions to flux data.⁴ Parameters fitted in this way generally depend on the underlying adopted model, and we have discussed how equilibrium concentrations can be extracted from such parameters in an earlier blog post. In Vl07 it is clear that the adopted mathematical and conceptual model is the effective porosity diffusion model. When first presented in the article, however, it is done so in terms of a sorption distribution coefficient (\(R_d\)) that is claimed to take on negative values for anions. The presented mathematical expressions therefore contain a so-called rock capacity factor, \(\alpha\), which relates to \(R_d\) as \(\alpha = \phi + \rho_d\cdot R_d\). But such use of a rock capacity factor is a mix-up of incompatible models that I have criticized earlier. However, in Vl07 the description involving a sorption coefficient is in words only — \(R_d\) is never brought up again — and all results are reported, interpreted and discussed in terms of effective (or “chloride-accessible”) porosity, labeled \(\epsilon\) or \(\epsilon_\mathrm{Cl}\). We here exclusively use the label \(\epsilon_\mathrm{eff}\) when referring to formulas in Vl07. The mathematics is of course the same regardless if we call the parameter \(\alpha\), \(\epsilon\), \(\epsilon_\mathrm{Cl}\), or \(\epsilon_\mathrm{eff}\).

Mass balance in the out-diffusion stage

Vl07 measured the amount of tracers accumulated in the two reservoirs during the out-diffusion stage. The flux into the left side reservoir, which served as source reservoir during the preceding through-diffusion stage, was completely obscured by significant amounts of tracers present in the confining filter, and will not be considered further (also Vl07 abandon this flux in their analysis). But the total amount of tracers accumulated in the right side reservoir, \(N_\mathrm{right}\),⁵ can be used to directly estimate the chloride equilibrium concentration.

The initial concentration profile in the out-diffusion stage is linear (it is the steady-state profile), and the total amount of tracers, \(N_\mathrm{tot}\),⁶ can be expressed

\begin{equation} N_\mathrm{tot} = \frac{\phi\cdot \bar{c}_0\cdot V_\mathrm{sample}} {2} \tag{3} \end{equation}

where \(\bar{c}_0\) is the initial clay concentration at the left side interface, and \(V_\mathrm{sample}\) (\(\approx\) 5 cm³) is the sample volume.

A neat feature of the out-diffusion process is that two thirds of the tracers end up in the left side reservoir, and one third in the right side reservoir, as illustrated in this simulation

\(\bar{c}_0\) can thus be estimated by using \(N_\mathrm{tot} = 3\cdot N_\mathrm{right}\) in eq. 3, giving

\begin{equation} \frac{\bar{c}_0}{c_\mathrm{source}} = \frac{6 \cdot N_\mathrm{right}} {\phi \cdot V_\mathrm{sample}\cdot c_\mathrm{source}} \tag{4} \end{equation}

where \(c_\mathrm{source}\) is the tracer concentration in the left side reservoir in the through-diffusion stage.⁷ Although eq. 4 depends on a particular solution to the diffusion equation, it is independent of diffusivity (the diffusivity in the above simulation is \(1\cdot 10^{-10}\) m²/s). Eq. 4 can in this sense be said to be a direct estimation of \(\bar{c}_0\) (from measured \(N_\mathrm{right}\)), although maybe not as “direct” as the measurement of stable chloride, discussed previously.

Vl07 state eq. 4 in terms of a “Cl-accessible porosity”, but this is still just an interpretation of the clay concentration; \(\bar{c}_0\) is, in contrast to \(\epsilon_\mathrm{eff}\), directly accessible experimentally in principle. From the reported values of \(\epsilon_\mathrm{eff}\) we may back-calculate \(\bar{c}_0\), using the relation \(\bar{c}_0 / c_\mathrm{source} = \epsilon_\mathrm{eff}/\phi\). Alternatively, we may use eq. 4 directly to evaluate \(\bar{c}_0\) from the reported values of \(N_\mathrm{right}\). Curiously, these two approaches result in slightly different values for \(\bar{c}_0/c_\mathrm{source}\). I don’t understand the cause for this difference, but since \(N_\mathrm{right}\) is what has actually been measured, we use these values to estimate \(\bar{c}_0.\) The resulting equilibrium concentrations are

Test	\(N_\mathrm{right}\) (10-10 mol)	\(\bar{c}_0/c_\mathrm{source}\) (-)
1.3/0.01	4.10	0.038
1.3/0.05	10.2	0.097
1.3/0.1	17.8	0.168
1.3/0.4	41.4	0.395
1.3/1.0	52.4	0.445
1.6/0.01	1.21	0.014
1.6/0.05	3.64	0.043
1.6/0.1	6.15	0.072
1.6/0.4	13.0	0.154
1.6/1.0	21.6	0.225
1.9/0.01	0.41	0.006
1.9/0.05	1.14	0.018
1.9/0.1	1.64	0.025
1.9/0.4	3.19	0.051
1.9/1.0	8.19	0.113

We have now investigated two independent estimations of the chloride equilibrium concentrations: from mass balance of chloride tracers in the out-diffusion stage, and from measured stable chloride content. Here are plots comparing these two estimations

The similarity is quite extraordinary! With the exception of two samples (1.3/0.4 and 1.9/0.1), the equilibrium chloride concentrations evaluated in these two very different ways are essentially the same. This result strongly confirms that the evaluations are adequate.

Steady-state fluxes

Vl07 present the flux evolution in the through-diffusion stage only for a single test (1.6/1.0), and it looks like this (left diagram)

The outflux reaches a relatively stable value after about 7 days, after which it is meticulously monitored for a quite long time period. The stable flux is not completely constant, but decreases slightly during the course of the test. We anyway refer to this part as the steady-state phase, and to the preceding part as the transient phase.

One reason that the steady-state is not completely stable is, reasonably, that the source reservoir concentration slowly decreases during the course of the test. The estimated drop from this effect, however, is only about one percent,⁸ while the recorded drop is substantially larger, about 7%. Vl07 do not comment on this perhaps unexpectedly large drop, but it may be caused e.g. by the ongoing conversion of the bentonite to a purer sodium state (see above).

Most of the analysis in Vl07 is based on anyway assigning a single value to the steady-state flux. Judging from the above plot, Vl07 seem to adopt the average value during the steady-state phase, and it is clear that the assigned value is well constrained by the measurements (the drop is a second order effect). The steady-state flux can therefore be said to be directly measured in the through-diffusion stage, rather than being obtained from fitting a certain model to data.

Vl07 only implicitly consider the steady-state flux, in terms of a fitted “effective diffusivity” parameter, \(D_e\) (more on this in the next section). We can, however, “de-derive” the corresponding steady-state fluxes using \(j_\mathrm{ss} = D_e\cdot c_\mathrm{source}/L\), where \(L\) (= 0.01 m) is sample length. When comparing different tests it is convenient to use the normalized steady state flux \(\widetilde{j}_\mathrm{ss} = j_\mathrm{ss}/c_\mathrm{source}\), which then relates to \(D_e\) as \(\widetilde{j}_\mathrm{ss} = D_e/L\). Indeed, “effective diffusivity” is just a scaled version of the normalized steady-state flux, and it makes more sense to interpret it as such (\(D_e\) is not a diffusion coefficient). From the reported values of \(D_e\) we obtain the following normalized steady-state fluxes (my apologies for a really dull table)

Test	\(D_e\) (10-12 m2/s)	\(\widetilde{j}_\mathrm{ss}\) (10-10 m/s)
1.3/0.01	2.6	2.6
1.3/0.05	7.5	7.5
1.3/0.1	16	16
1.3/0.4	25	25
1.3/1.0	49	49
1.6/0.01	0.39	0.39
1.6/0.05	1.1	1.1
1.6/0.1	2.3	2.3
1.6/0.4	4.6	4.6
1.6/1.0	10	10
1.9/0.01	0.033	0.033
1.9/0.05	0.12	0.12
1.9/0.1	0.24	0.24
1.9/0.4	0.5	0.5
1.9/1.0	1.2	1.2

Plotting \(\widetilde{j}_\mathrm{ss}\) as a function of background concentration gives the following picture

The steady-state flux show a very consistent behavior: for all three densities, \(\widetilde{j}_\mathrm{ss}\) increases with background concentration, with a higher slope for the three lowest background concentrations, and a smaller slope for the two highest background concentrations. Although we have only been able to investigate the 1.6/1.0 test in detail, this consistency confirms that the steady-state flux has been reliably determined in all tests.

Transient phase evaluations

So far, we have considered estimations based on more or less direct measurements: stable chloride concentration profiles, tracer mass balance in the out-diffusion stage, and steady-state fluxes. A major part of the analysis in Vl07, however, is based on fitting solutions of the diffusion equation to the recorded flux.

Vl07 state somewhat different descriptions for the through- and out-diffusion stages. For out-diffusion they use an expression for the flux into the right side reservoir (the sample is assumed located between \(x=0\) and \(x=L\))

\begin{equation} j(L,t) = -2\cdot j_\mathrm{ss} \sum_{n = 1}^\infty \left(-1\right )^n\cdot e^{-\frac{D_e\cdot n^2\cdot \pi^2\cdot t} {L^2\cdot \epsilon_\mathrm{eff}}} \tag{5} \end{equation}

where \(j_\mathrm{ss}\) is the steady-state flux,⁹ \(D_e\) is “effective diffusivity”, and \(\epsilon_\mathrm{eff}\) is the effective porosity parameter (Vl07 also state a similar expression for the diffusion into the left side reservoir, but these results are discarded, as discussed earlier). For through-diffusion, Vl07 instead utilize the expression for the amount tracer accumulated in the right side reservoir

\begin{equation} A(L,t) = S\cdot L \cdot c_\mathrm{source} \left ( \frac{D_e\cdot t}{L^2} – \frac{\epsilon_\mathrm{eff}} {6} – \frac{2\cdot\epsilon_\mathrm{eff}}{\pi^2} \sum_{n = 1}^\infty \frac{\left(-1\right )^n}{n^2} \cdot e^{-\frac{D_e\cdot n^2\cdot \pi^2\cdot t} {L^2\cdot \epsilon_\mathrm{eff}} }\right ) \tag{6} \end{equation}

were \(S\) denotes the cross section area of the sample.

It is clear that Vl07 use \(D_e\) and \(\epsilon_\mathrm{eff}\) as fitting parameters, but not exactly how the fitting was conducted. \(D_e\) seems to have been determined solely from the the through-diffusion data, while separate values are evaluated for \(\epsilon_\mathrm{eff}\) from the through- and out-diffusion stages. As already discussed, Vl07 also provide a third estimation of \(\epsilon_\mathrm{eff}\), based on mass-balance in the out-diffusion stage. To me, the study thereby gives the incorrect impression of providing a whole set of independent estimations of \(\epsilon_\mathrm{eff}\). Although eqs. 5 and 6 are fitted to different data, they describe diffusion in one and the same sample, and an adequate fitting procedure should provide a consistent, single set of fitted parameters \((D_e, \epsilon_\mathrm{eff})\). Even more obvious is that the estimation of \(\epsilon_\mathrm{eff}\) from fitting eq. 5 should agree with the estimation from the mass-balance in the out diffusion stage — the accumulated amount in the right side reservoir is, after all, given by the integral of eq. 5. A significant variation of the reported fitting parameters for the same sample would thus signify internal inconsistency (experimental- or modelwise).

In the following reevaluation we streamline the description by solely using fluxes as model expressions,⁴ and by emphasizing steady-state flux as a parameter, which I think gives particularly neat expressions,¹⁰ (“TD” and “OD” denote through- and out-diffusion, respectively)

\begin{equation} \widetilde{j}_{TD}(L,t) = \widetilde{j}_\mathrm{ss} \left ( 1 + 2 \sum_{n = 1}^\infty \left(-1\right )^n \cdot e^{-\frac{D_p\cdot n^2\cdot \pi^2\cdot t} {L^2} }\right ) \tag{7} \end{equation}

\begin{equation} \widetilde{j}_{OD}(L,t) = -2\cdot \widetilde{j}_\mathrm{ss} \sum_{n = 1}^\infty \left( -1 \right )^n \cdot e^{-\frac{D_p\cdot n^2\cdot \pi^2\cdot t} {L^2}} \tag{8} \end{equation}

Here we use the pore diffusivity, \(D_p\), instead of the combination \(D_e/\epsilon_\mathrm{eff}\) in the exponential factors, and \(\widetilde{j} = j/c_\mathrm{source}\) denotes normalized flux. This formulation clearly shows that the time evolution is governed solely by \(D_p\), and that \(\widetilde{j}_\mathrm{ss}\) simply acts as a scaling factor.

In my opinion, using \(\widetilde{j}_\mathrm{ss}\) and \(D_p\) gives a formulation more directly related to measurable quantities; the steady-state flux is directly accessible experimentally, as we just examined, and \(D_p\) is an actual diffusion coefficient (in contrast to \(D_e\)) that can be directly evaluated from clay concentration profiles. Of course, eqs. 7 and 8 provide the same basic description as eqs. 5 and 6, and \(\widetilde{j}_\mathrm{ss}\) and \(D_p\) are related to the parameters reported in Vl07 as

\begin{equation} \widetilde{j}_\mathrm{ss} = \frac{D_e}{L} \tag{9} \end{equation}

\begin{equation} D_p = \frac{D_e}{\epsilon_\mathrm{eff}} \tag{10} \end{equation}

When reevaluating the reported data we focus on the above discussed consistency aspect, i.e. whether or not a single model (a single pair of parameters) can be satisfactory fitted to all available data for the same sample. In this regard, we begin by noting that the fitting parameters are already constrained by the direct estimations. We have already concluded that the recorded steady-state flux basically determines \(\widetilde{j}_\mathrm{ss}\), and if we combine this with the estimated chloride clay concentration, \(D_p\) is determined from \(j_\mathrm{ss} = \phi\cdot D_p\cdot \bar{c}_0/L\), i.e.

\begin{equation} D_p = \frac{\widetilde{j}_\mathrm{ss}\cdot L} {\phi\cdot \left (\bar{c}_0 / c_\mathrm{source}\right )} \tag{11} \end{equation}

Here are plotted values of \(D_p\) evaluated in this manner

Note that these values basically remain constant for samples of similar density (within a factor of 2) as the background concentration is varied by two orders of magnitude. This is the expected behavior of an actual diffusion coefficient,¹¹ and confirms the adequacy of the evaluation; the numerical values also compares rather well with corresponding values for “MX-80” bentonite, measured in closed-cell tests (indicated by dashed lines in the figure).

Using eq. 10, we can also evaluate values of \(D_p\) corresponding to the various reported fitted parameters \(\epsilon_\mathrm{eff}\). The result looks like this (compared with the above evaluations from direct estimations)

As pointed out above, a consistent evaluation requires that the parameters fitted to the out-diffusion flux (red) are very similar to those evaluated from considering the mass balance in the same process (blue). We note that the resemblance is quite reasonable, although some values — e.g. tests 1.3/1.0 and 1.6/1.0 — deviate in a perhaps unacceptable way.

\(D_p\) evaluated from reported through-diffusion parameters, on the other hand, shows significant scattering (green). As the rest of the values are considerably more collected, and as the steady-state fluxes show no sign whatsoever that the diffusion coefficient varies in such erratic manner, it is quite clear that this scattering indicates problems with the fitting procedure for the through-diffusion data.

The 1.6/1.0 test

To further investigate the fitting procedures, we take a detailed look at the 1.6/1.0 test, for which flux data is provided. Vl07 report fitted parameters \(D_e = 1.0\cdot 10^{-11}\) m²/s and \(\epsilon_\mathrm{eff} = 0.063\) to the through-diffusion data, corresponding to \(\widetilde{j}_\mathrm{ss} = 1.0\cdot 10^{-9}\) m/s and \(D_p = 1.6\cdot 10^{-10}\) m²/s. We have already concluded that the steady-state flux is well captured by this data, but to see how well fitted \(\epsilon_\mathrm{eff}\) (or \(D_p\)) is, lets zoom in on the transient phase

This diagram also contains models (eq. 7) with different values of \(D_p\), and with a slightly different value of \(j_\mathrm{ss}\).¹² It is clear that the model presented in the paper (black) completely misses the transient phase, and that a much better fit is achieved with \(D_p = 9.7\cdot10^{-11}\) m²/s (and \(\widetilde{j}_\mathrm{ss} = 1.06\cdot 10^{-9}\) m/s) (red). This difference cannot be attributed to uncertainty in the parameter \(D_p\) — the reported fit is simply of inferior quality. With that said, we note that all information on the transient phase is contained within the first three or four flux points; the reliability could probably have been improved by measuring more frequently in the initial stage.¹³

A reason for the inferior fit may be that Vl07 have focused only on the linear part of eq. 6; the paper spends half a paragraph discussing how the approximation of this expression for large \(t\) can be used to extract the fitting parameters using linear regression. Does this mean that only experimental data for large times where used to evaluate \(D_e\) and \(\epsilon_\mathrm{eff}\)? Since we are not told how fitting was performed, we cannot answer this question. Under any circumstance, the evidently low quality of the fit puts in question all the reported \(\epsilon_\mathrm{eff}\) values fitted to through-diffusion data. This is actually good news, as several of the corresponding \(D_p\) values were seen to be incompatible with constraints from direct estimations. We can thus conclude with some confidence that the inconsistency conveyed by the differently evaluated fitting parameters does not indicate experimental shortcomings, but stems from bad fitting of the through-diffusion model. Therefore, we simply dismiss the reported \(\epsilon_\mathrm{eff}\) values evaluated in this way. Note that the re-fitted value for \(D_p\) \((9.7\cdot10^{-11}\) m²/s) is consistent with those evaluated from direct estimations.

We note that when fitting the transient phase, it is appropriate to use a value of \(\widetilde{j}_\mathrm{ss}\) slightly larger than the average value adopted by Vl07 (as the model does not account for the observed slight drop of the steady-state flux). This is only a minor variation in the \(\widetilde{j}_\mathrm{ss}\) parameter itself (from \(1.02\cdot10^{-9}\) to \(1.06\cdot10^{-9}\) m/s), but, since this value sets the overall scale, it indirectly influences the fitted value of \(D_p\) (model fitting is subtle!).

More questions arise regarding the fitting procedures when also examining the presented out-diffusion stage for the 1.6/1.0 sample. The tabulated fitted value for this stage is \(\epsilon_\mathrm{eff}\) = 0.075, while it is implied that the same value has been used for \(D_e\) as evaluated from the the through-diffusion stage (\(1.0\cdot 10^{-11}\) m²/s). The corresponding pore diffusivity is \(D_p = 1.33\cdot 10^{-10}\) m²/s. The provided plot, however, contains a different model than tabulated, and looks similar to this one (left diagram)

Here the presented model (black dashed line) instead corresponds to \(D_p = 8.5\cdot 10^{-11}\) m²/s (or \(\epsilon_\mathrm{eff}\) = 0.118). The model corresponding to the tabulated value (orange) does not fit the data! I guess this error may just be due to a typo in the table, but it nevertheless gives more reasons to not trust the reported \(\epsilon_\mathrm{eff}\) values fitted to diffusion data.

The above diagram also shows the model corresponding to the reported parameters from the through-diffusion stage (black solid line). Not surprisingly, this model does not fit the out-diffusion data, confirming that it does not appropriately describe the current sample. The model we re-fitted in the through-diffusion stage (red), on the other hand, captures the outflux data quite well. By also slightly adjusting \(\widetilde{j}_{ss}\), from from \(1.06\cdot10^{-9}\) to \(0.99\cdot10^{-9}\) m/s, to account for the drop in steady-state flux during the course of the through-diffusion test, and by plotting in a lin-lin rather than a log-log diagram, the picture looks even better! In a lin-lin plot (right diagram), it is easier to note that the model presented in the graph of Vl07 actually misses several of the data points. Could it be that Vl07 used visual inspection of the model in a log-log diagram to assess fitting quality? If so, data points corresponding to very low fluxes are given unreasonably high weight.¹⁴ This could be (another) reason for the noted difference between \(D_p\) evaluated from fitted parameters to the out-diffusion flux, and from the total accumulated amount of tracer (which should be equal).

From examining the reported results of sample 1.6/1.0 we have seen that the fitting procedures adopted in Vl07 appear inappropriate, but also that a consistent model can be successfully fitted to all available data (using a single \(D_p\)). Vl07 don’t provide flux data for any other sample, but we must conclude that the reported fitted \(\epsilon_\mathrm{eff}\) parameters cannot be trusted. Luckily, the preformed refitting exercise confirms the results obtained from analysis of stable chloride profiles and accumulated amount of tracers in out-diffusion, and we conclude that these results most probably are reliable. The corresponding value of \(\bar{c}_0/c_\mathrm{source}\) (using eq. 11) for the refitted model is here compared with the estimations from direct measurements

Summary and verdict

Chloride equilibrium concentrations evaluated from mass balance of the tracer in the out-diffusion stage and from stable chloride content show remarkable agreement. On the other hand, the scattering of estimated concentrations increases substantially if they are also evaluated from the reported fitted diffusion parameters. This could indicate underlying experimental problems, as a consistent evaluation should result in a single value for the equilibrium concentration; the various evaluations — stable chloride, out-diffusion mass balance, through-diffusion fitting and out-diffusion fitting — relate, after all, to a single sample.

By reexamining the evaluations we have found, however, that the problem is associated with how the fitting to diffusion data has been conducted (and presented), rather than indicating fundamental experimental issues. In the test that we have been able to examine in detail (1.6/1.0), we found that the reported models do not fit data, but also that it is possible to satisfactorily refit a single model that is also compatible with the direct methods for evaluating the equilibrium concentration. For the rest of the samples, we have also been able to discard the fitted diffusion parameters, as they are not compatible e.g. with how the steady-state flux (very consistently) vary with density and background concentration.

For these reasons, we discard the reported “effective porosity” parameters evaluated from fitting solutions of the diffusion equation to flux data, and keep the results from direct measurements of chloride equilibrium concentrations (from stable chloride profile analysis and mass-balance in the out-diffusion stage). I judge the resulting chloride equilibrium concentrations as reliable and that they can be used for increased qualitative process understanding. I furthermore judge the directly measured steady-state fluxes as reliable. This study thus provide adequate values for both chloride equilibrium concentrations and diffusion coefficients.

However, a frustrating problem is that, although the equilibrium concentrations are well determined, we have little information on the exact state of the samples in which they have been measured. We basically have to rely on that the “KWK” material is “similar” to “MX-80”, keeping in mind that “MX-80” is not really a uniform material (from a scientific point of view). Also, the exchangeable mono/divalent cation ratio is most probably quite different in samples contacted with different background concentrations.

Yet, I judge the present study to provide the best information available on chloride equilibrium in compacted bentonite, and will use it e.g. for investigating the salt exclusion mechanism in these systems (I already have). That this information is the best available is, however, also a strong argument for that more and better constrained data is urgently needed.

The (reliable) results are presented in the diagram below, which includes “confidence areas”, that takes into account the spread in equilibrium concentrations, in samples where more than a single evaluation were performed, and the estimated uncertainty in effective montmorillonite dry density (the actual points are plotted at nominal density, assuming 80% montmorillonite content)

• Chloride content: UNKNOWN
• Extracting anion equilibrium concentrations from through-diffusion tests
• Assessment of chloride equilibrium concentrations: Muurinen et al. (1988)
• Assessment of chloride equilibrium concentrations: Molera et al. (2003)
• How salt equilibrium concentrations may be overestimated
• Assessment of chloride equilibrium concentrations: Muurinen et al. (2004)

Footnotes

[1] Vejsada et al. (2006) call their material “KWK 20-80”. In other contexts, I have also found the versions “KWK food grade” and “KWK krystal klear”. I have given up my attempts at trying to understand the difference between these “KWK” variants.

[2] Van Loon et al. (2007) label the background concentration \([\mathrm{Cl}]_0\).

[3] This should be relatively straightforward, but I get at bit nervous e.g. about the presence of a rather arbitrary factor 0.85 in the presented formula (eq. 19 in Van Loon et al. (2007)).

[4] As always for these types of diffusion tests, the raw data consists of simultaneously measured values of time (\(\{t_i\}\)) and reservoir concentrations (\(\{c_i\}\)). From these, flux can be evaluated as (\(A\) is sample cross sectional area, and \(V_\mathrm{res}\) is reservoir volume)

\begin{equation} \bar{j}_i = \frac{1}{A} \frac{ \left (c_i – c_{i-1} \right ) \cdot V_\mathrm{res}} {t_i – t_{i-i}} \tag{*} \end{equation}

\(\bar{j}_i\) is the mean flux in the time interval between \(t_{i-1}\) and \(t_i\), and should be associated with the average time of the same interval: \(\bar{t}_i = (t_i + t_{i-1})/2\). The above formula assumes no solution replacement after the \((i-1)\):th measurement (if the solution is replaced, \(\left (c_i – c_{i-1} \right )\) should be replaced with \(c_i\)).

Alternatively one can work with the accumulated amount of substance, which e.g. is \(N(t_i) = \sum_{j=1}^i c_j\cdot V_\mathrm{res}\), in case the solution is replaced after each measurement. I prefer using the flux because eq. * only depends on two consecutive measurements, while \(N(t_i)\) in principle depends on all measurements up to time \(t_i\). Also, I think it is easier to judge how well e.g. a certain model fits or is constrained by data when using fluxes; the steady-state, for example, then corresponds to a constant value.

Van Loon et al. (2007) seem to have utilized both fluxes and accumulated amount of substance in their evaluations, as discussed in later sections.

[5] Van Loon et al. (2007) denote this quantity \(A(L)\).

[6] Van Loon et al. (2007) denote this quantity \(A_w\), \(A_\mathrm{out}\), and \(A_\mathrm{tot}\).

[7] Van Loon et al. (2007) denote this quantity \(C_0\).

[8] From total test time, recorded flux, and sample cross sectional area, we estimate that about \(5.8\cdot 10^{-8}\) mol of tracer is transferred from the source reservoir during the course of the test (\(50\) days\(\cdot 2.7\cdot 10^{-11}\) mol/m²/s\(\cdot 0.0005\) m²). This is about 1% of the total amount tracer, \(c_\mathrm{source} \cdot V_\mathrm{source} = 2.65 \cdot 10^{-5}\) M \(\cdot 0.2\) L = \(5.3\cdot 10^{-6}\) mol.

[9] Van Loon et al. (2007) label this parameter \(J_L\), and don’t relate it explicitly to the steady-state flux. From the experimental set-up it is clear, however, that the initial value of the out-diffusion flux (into the right side reservoir) is the same as the previously maintained steady-state flux. Note that the expressions for the fluxes in the out-diffusion stage in Van Loon et al. (2007) has the wrong sign.

[10] The description provided by eqs. 5 and 6 not only mixes expressions for flux and accumulated amount tracer, but also contains three dependent parameters \(D_e\), \(\epsilon_\mathrm{eff}\), and \(j_\mathrm{ss}\) (e.g. \(j_\mathrm{ss} = D_e/(c_\mathrm{source}\cdot L)\)). In this reformulation, the model parameters are strictly only \(\widetilde{j}_\mathrm{ss}\) and \(D_p\). We have also divided out \(c_\mathrm{source}\) to obtain equations for normalized fluxes. Note that the expression for \(\widetilde{j}_{TD}(L,t)\) is essentially the same that we have used in previous assessments of through-diffusion tests. Note also that eqs. 7 and 8 imply the relation \(\widetilde{j}_{OD}(L,t) = \widetilde{j}_{ss} – \widetilde{j}_{TD}(L,t)\), reflecting that the out-diffusion process is essentially the through-diffusion process in reverse.

[11] Note the similarity with that diffusivity also is basically independent of background concentration for simple cations. Note also that there is no reason to expect completely constant \(D_p\) for a given density, because the samples are not identically prepared (being saturated with saline solutions of different concentration).

[12] As we here consider a single sample, we alternate a bit sloppily between steady-state flux (\(j_\mathrm{ss} \)) and normalized steady-state flux (\(\widetilde{j}_\mathrm{ss}\)), but these are simply related by a constant: \(\widetilde{j}_\mathrm{ss} = j_\mathrm{ss} / c_\mathrm{source}\). For the 1.6/1.0 test this constant is (as tabulated) \(c_\mathrm{source} = 2.65\cdot 10^{-2}\) mol/m³.

[13] I think it is a bit amusing that the pattern of data points suggests measurements being performed on Mondays, Wednesdays, and Fridays (with the test started on a Wednesday).

[14] I have warned about the dangers of log-log plots earlier.

In the ongoing assessment of chloride equilibrium concentrations in bentonite, we here take a closer look at the study by Molera et al. (2003), in the following referred to as Mo03. We thus assess the 13 points indicated here

Mo03 performed both chloride and iodide through-diffusion tests on “MX-80” bentonite, but here we focus on the chloride results. However, since the only example in the paper of an outflux evolution and corresponding concentration profile is for iodide, this particular result will also be investigated. The tests were performed at background concentrations of 0.01 M or 0.1 M NaClO₄, and nominal sample densities of 0.4, 0.8, 1.2, 1.6, and 1.8 g/cm³. We refer to a single test by stating “nominal density/background concentration”, e.g. a test performed at nominal density 1.6 and background concentration 0.1 M is referred to as “1.6/0.1”.

Uncertainty of samples

The material used is discussed only briefly, and the only reference given for its properties is (Müller-Von Moos and Kahr, 1983). I don’t find any reason to believe that the “MX-80” batch used in this study actually is the one investigated in this reference, and have to assume the same type of uncertainty regarding the material as we did in the assessment of Muurinen et al (1988). I therefore refer to that blog post for a discussion on uncertainty in montmorillonite content, cation population, and soluble calcium minerals.

Density

The samples in Mo03 are cylindrical with radius 0.5 cm and length 0.5 cm, giving a volume of 0.39 cm³. This is quite small, and corresponds e.g. only to about 4% of the sample size used in Muurinen et al (1988). With such a small volume, the samples are at the limit for being considered as a homogeneous material, especially for the lowest densities: the samples of density 0.4 g/cm³ contain 0.157 g dry substance in total, while a single 1 mm³ accessory grain weighs about 0.002 — 0.003 g.

Furthermore, as the samples are sectioned after termination, the amount substance in each piece may be very small. This could cause additional problems, e.g. enhancing the effect of drying. The reported profile (1.6/0.1, iodide diffusion) has 10 sections in the first 2 mm. As the total mass dry substance in this sample is 0.628 g, these sections have about 0.025 g dry substance each (corresponding to the mass of about ten 1 mm³ grains). For the lowest density, a similar sectioning corresponds to slices of dry mass 0.006 g (the paper does not give any information on how the low density samples were sectioned).

Mo03 only report nominal densities for the samples, but from the above considerations it is clear that a substantial (but unknown) variation may be expected in densities and concentrations.

A common feature of many through-diffusion studies is that the sample density appears to decrease in the first few millimeters near the confining filters. We saw this effect in the profiles of Muurinen et al (1988), and it has been the topic of some studies, including Mo03. Here, we don’t consider any possible cause, but simply note that the samples seem to show this feature quite generally (below we discuss how Mo03 handle this). Since the samples of Mo03 are only of length 5 mm, we may expect that the major part of them are affected by this effect. Of course, this increases the uncertainty of the actual density of the used samples.

Uncertainty of external solutions

Mo03 do not describe how the external solutions were prepared, other than that they used high grade chemicals. We assume here that the preparation did not introduce any significant uncertainty.

Since “MX-80” contains a substantial amount of divalent ions, connecting this material with (initially) pure sodium solutions inevitably initiates cation exchange processes. The extent of this exchange depends on details such as solution concentrations, reservoir volumes, number of solution replacements, time, etc…

Very little information is given on the volume of the external solution reservoirs. It is only hinted that the outlet reservoir may be 25 ml, and for the inlet reservoir the only information is

The volume of the inlet reservoir was sufficient to keep the concentration nearly constant (within a few percent) throughout the experiments.

Consequently, we do not have enough information to assess the exact ion population during the course of the tests. We can, however, simulate this process of “unintentional exchange” to get some appreciation for the amount of divalent ions still left in the sample, as we did in the assessment of Muurinen et al. (1988). Here are the results from calculating the exchange equilibrium between a sample initially containing 30% exchangeable charge in form of calcium (70% sodium), and external NaClO₄ solutions of various concentrations and volumes

In these calculations we assume a sample of density 1.6 g/cm³ (except when indicated), a volume of 0.39 cm³, a cation exchange capacity of 0.75 eq/kg, and a Ca/Na selectivity coefficient of 5.

These simulations make it clear that the tests performed at 0.01 M most probably contain most of the divalent ions initially present in the “MX-80” material: even with an external solution volume of 1000 ml, or with density 0.4 g/cm³, exchange is quite limited. For the tests performed at 0.1 M we expect some exchange of the divalent ions, but we really can’t tell to what extent, as the exact value strongly depends on handling (solution volumes, if solutions were replaced, etc.). That the exact ion population is unknown, and that the divalent/monovalent ratio probably is different for different samples, are obviously major problems of the study (the same problems were identified in Muurinen et al (1988)).

Uncertainty of diffusion parameters

Diffusion model

Mo03 determine diffusion parameters by fitting a model to all available data, i.e the outflux evolution and the concentration profile across the sample at termination. The model is solved by a numerical code (“ANADIFF”) that takes into account transport both in clay samples and filters. The fitted parameters are an apparent diffusivity, \(D_a\), and a so-called “capacity factor”, \(\alpha\). \(\alpha\) is vaguely interpreted as being the combination of a porosity factor \(\epsilon\), and a sorption distribution coefficient \(K_d\), described as “a generic term devoid of mechanism”

\begin{equation} \alpha = \epsilon + \rho\cdot K_d \end{equation}

It is claimed that for anions, \(K_d\) can be treated as negative, giving \(\alpha < \epsilon\). I have criticized this mixing of what actually are incompatible models in an earlier blog post. Strictly, this use of a “generic term devoid of mechanism” means that the evaluated \(\alpha\) should not be interpreted in any particular way. Nevertheless, the way this study is referenced in other publications, \(\alpha\) is interpreted as an effective porosity. It should be noticed, however, that this study is performed with a background electrolyte of NaClO₄. The only chloride (or iodide) present is therefore at trace level, and it cannot be excluded that a mechanism of true sorption influences the results (there are indications that this is the case in other studies).

For the present assessment we anyway assume that \(\alpha\) directly quantifies the anion equilibrium between clay and the external solution (i.e. equivalent to the incorrect way of assuming that \(\alpha\) quantifies a volume accessible to chloride). It should be kept in mind, though, that effects of anion equilibrium and potential true sorption is not resolved by the single parameter \(\alpha\).

In practice, then, the model is

\begin{equation} \frac{\partial c}{\partial t} = D_p\frac{\partial^2 c}{\partial x^2} \tag{1} \end{equation}

where \(c\) is the concentration in the clay of the isotope under consideration, and the diffusion coefficient is written \(D_p\) to acknowledge that it is a pore diffusivity (when referring to models and parameter evaluations in Mo03 we will use the notation “\(D_a\)”). The boundary conditions are

\begin{equation} c(0,t) = \alpha \cdot C_0 \;\;\;\; c(L,t) = 0 \tag{2} \end{equation}

where \(C_0\) is the concentration in the source reservoir,¹ and \(L\) is the sample length.

This model — that we have discussed before — has a relatively simple analytical solution, and the outflux can be written

\begin{equation} j^\mathrm{out}(t) = j^\mathrm{ss}\left (1 + 2 \sum_{n=1}^\infty \left (-1 \right )^n e^{-\frac{\pi^2n^2D_pt}{L^2}} \right) \end{equation}

where \(j^\mathrm{ss}\) is the corresponding steady-state flux. Here, the steady-state flux is related to the other parameters as

\begin{equation} j^\mathrm{ss} = \alpha\cdot D_p \frac{C_0}{L} \tag{3} \end{equation}

“Fast” and “slow” processes

Oddly, Mo03 model the system as if two independent diffusion processes are simultaneously active. They refer to these as the “fast” and the “slow” processes, and hypothesize that they relate to diffusion in interlayer water² and “interparticle water”,³ respectively.

The “fast” process is the “ordinary” process that is assumed to reach steady state during the course of the test, and that is the focus of other through-diffusion studies. The “slow” process, on the other hand, is introduced to account for the frequent observation that measured tracer profiles are usually significantly non-linear near the interface to the source reservoir (discussed briefly above). I guess that the reason for this concentration variation is due to swelling when the sample is unloaded. But even if the reason is not fully clear, it can be directly ruled out that it is the effect of a second, independent, diffusion process — because this is not how diffusion works!

If anions move both in interlayers and “interparticle water”, they reasonably transfer back and forth between these domains, resulting in a single diffusion process (the diffusivity of such a process depends on the diffusivity of the individual domains and their geometrical configuration). To instead treat diffusion in each domain as independent means that these processes are assumed to occur without transfer between the domains, i.e. that the bentonite is supposed to contain isolated “interlayer pipes”, and “interparticle pipes”, that don’t interact. It should be obvious that this is not a reasonable assumption. Incidentally, this is how all multi-porous models assume diffusion to occur (while simultaneously assuming that the domains are in local equilibrium…).

We will thus focus on the “fast” process in this assessment, although we also use the information provided by the parameters for the “slow” process. Mo03 report the fitted values for \(D_a\) and \(\alpha\) in a table (and diagrams), and only show a comparison between model and measured data in a single case: for iodide diffusion at 0.1 M background concentration and density 1.6 g/cm³. To make any kind of assessment of the quality of these estimations we therefore have to focus on this experiment (the article states that these results are “typical high clay density data”).

Outflux

The first thing to note is that the modeled accumulated diffusive substance does not correspond to the analytical solution for the diffusion process. Here is a figure of the experimental data and the reported model (as presented in the article), that also include the solution to eqs. 1 and 2.

In fact, the model presented in Mo03 has an incorrect time dependency in the early stages. Here is a comparison between the presented model and analytical solutions in the transient stage

With the given boundary conditions, the solutions to the diffusion equation inevitably has zero slope at \(t = 0\),⁴ reflecting that it takes a finite amount of time for any substance to reach the outflux boundary. The models presented in Mo03, on the other hand, has a non-zero slope in this limit. I cannot understand the reason for this (is it an underlying problem with the model, or just a graphical error?), but it certainly puts all reported parameter values in doubt.

The preferred way to evaluate diffusion data is, in my opinion, to look at the flux evolution rather than the evolution of the accumulated amount of diffused substance. Converting the reported data to flux, gives the following picture.⁵

From a flux evolution it is easier to establish the steady-state, as it reaches a constant. It furthermore gives a better understanding for how well constrained the model is by the data. As is seen from the figure, the model is not at all very well constrained, as the experimental data almost completely miss the transient stage. (And, again, it is seen that the model in the paper with \(D_a= 9\cdot 10^{-11}\) m/s² does not correspond to the analytical solution.)

The short transient stage is a consequence of using thin samples (0.5 cm). Compared e.g. to Muurinen et al (1988), who used three times as long samples, the breakthrough time is here expected to be \(3^2 = 9\) times shorter. As Muurinen et al. (1988) evaluated breakthrough times in the range 1 — 9 days, we here expect very short times. Here are the breakthrough times for all chloride diffusion tests, evaluated from the reported diffusion coefficients (“fast” process) using the formula \(t_\mathrm{bt} = L^2/(6D_a)\).

Test	\(D_a\)	\(t_\mathrm{bt}\)
	(m2/s)	(days)
0.4/0.01	\(8\cdot 10^{-10}\)	0.06
0.4/0.1	\(9\cdot 10^{-10}\)	0.05
0.4/0.1	\(8\cdot 10^{-10}\)	0.06
0.8/0.01	\(3.5\cdot 10^{-10}\)	0.14
0.8/0.1	\(3.5\cdot 10^{-10}\)	0.14
0.8/0.1	\(3.7\cdot 10^{-10}\)	0.13
1.2/0.01	\(1.4\cdot 10^{-10}\)	0.34
1.2/0.1	\(2.3\cdot 10^{-10}\)	0.21
1.2/0.1	\(2.0\cdot 10^{-10}\)	0.24
1.6/0.1	\(1.0\cdot 10^{-10}\)	0.48
1.8/0.01	\(2\cdot 10^{-11}\)	2.41
1.8/0.1	\(5\cdot 10^{-11}\)	0.96
1.8/0.1	\(5.5\cdot 10^{-11}\)	0.88

The breakthrough time is much shorter than a day in almost all tests! To sample the transient stage properly requires a sampling frequency higher than \(1/t_{bt}\). As seen from the provided example of a outflux evolution, this is not the case: The second measurement is done after about 1 day, while the breakthrough time is about 0.5 days (moreover, the first measurement appears as an outlier). We have no information on sampling frequency in the other tests, but note that to properly sample e.g. the tests at 0.8 g/cm³ requires measurements at least every third hour or so. For 0.4 g/cm³, the required sample frequency is once an hour! This design choice puts more doubt on the quality of the evaluated parameters.

Concentration profile

The measured concentration profile across the 1.6/0.1 iodide sample, and corresponding model results are presented in Mo03 in a figure very similar to this

Here the two models correspond to the “slow” and “fast” process discussed above (a division, remember, that don’t make sense). Zooming in on the “linear” part of the profile, we can compare the “fast” process with analytical solutions (eqs. 1 and 2)

The analytical solutions correspond directly to the outflux curves presented above. We note that the analytical solution with \(D_p = 9\cdot 10^{-11}\) m/s² corresponds almost exactly to the model presented by Mo03. As this model basically has the same steady state flux and diffusion coefficient, we expect this similarity. It is, however, still a bit surprising, since the corresponding outflux curve of the model in Mo03 was seen to not correspond to the analytical solution. This continues to cast doubt on the model used for evaluating the parameters.

We furthermore note that the evolution of the activity of the source reservoir is not reported. Once in the text is mentioned that the “carrier concentration” is \(10^{-6}\) M, but since we don’t know how much of this concentration corresponds to the radioactive isotope, we can not directly compare with reported concentration profile across the sample (whose concentration unit is counts per minute per cm³). By extrapolating the above model curve with \(\alpha = 0.15\), we can however deduce that the corresponding source activity for this particular sample is \(C_0 = 1.26\cdot 10^5/0.15\) cpu/cm³ \(= 8.40\cdot 10^5\) cpu/cm³. But it is unsatisfying that we cannot check this independently. Also, we can of course not assume that this value of \(C_0\) is the same in any other of the tests (in particular those involving chloride). We thus lack vital information (\(C_0\)) to be able to make a full assessment of the model fitting.

It should furthermore be noticed that the experimental concentration profile does not constrain the models very well. Indeed, the adopted model (diffusivity \(9\cdot 10^{-11}\) m/s²) misses the two rightmost concentration points (which correspond to half the sample!). A model that fits this part of the profile has a considerable higher diffusivity, and a correspondingly lower \(\alpha\) (note that the product \(D_p\cdot \alpha\) is constrained by the steady-state flux, eq. 3).

More peculiarities of the modeling is found if looking at the “slow” process (remember that this is not a real diffusion process!). Zooming in on the interface part of the profile and comparing with analytical solutions gives this picture

Here we note that an analytical solution coincides with the model presented in Mo03 with parameters \(D_a = 6\cdot 10^{-14}\) m²/s and \(\alpha = 1.12\) only if it is propagated for about 15 days! Given that no outflux measurements seem to have been performed after about 4 days (see above), I don’t now what to make of this. Was the test actually conducted for 15 days? If so, why is not more of the outflux measured/reported? (And why were the samples then designed to give a breakthrough time of only a few hours?)

Without knowledge of for how long the tests were conducted, the reported diffusion parameters becomes rather arbitrary, especially for the low density samples. For e.g. the samples of density 0.4 g/cm³, even the “slow” process has a diffusivity high enough to reach steady-state within a few days. Simulating the processes with the reported parameters gives the following profiles if evaluated after 1 and 4 days, respectively

The line denoted “total” is what should resemble the measured (unreported) data. It should be clear from these plots that the division of the profile into two separate parts is quite arbitrary. It follows that the evaluated diffusion parameters for the process of which we are interested (“fast”) has little value.

Summary and verdict

We have seen that the reported model fitting leaves a lot of unanswered questions: some of the model curves don’t correspond to the analytical solutions, information on evolution times and source concentrations is missing, and the modeled profiles are divided quite arbitrary into two separate contributions (which are not two independent diffusion process).

Moreover, the ion population (divalent vs. monovalent cations) of the samples are not known, but there are strong reasons to believe that the 0.01 M tests contain a significant amount of divalent ions, while the 0.1 M samples are partly converted to a more pure sodium state.

Also, the small size of the samples contributes to more uncertainty, both in terms of density, but also for the flux evolution because the breakthrough times becomes very short.

Based on all of these uncertainties, I mean that the results of Mo03 does not contribute to quantitative process understanding and my decision is to not to use the study for e.g. validating models of anion exclusion.

A confirmation of the uncertainty in this study is given by considering the density dependence on the chloride equilibrium concentrations for constant background concentration, evaluated from the reported diffusion parameters (\(\alpha\) for the “fast” process).

If these results should be taken at face value, we have to accept a very intricate density dependence: for 0.1 M background, the equilibrium concentration is mainly constant between densities 0.3 g/cm³ and 0.7 g/cm³, and increases between densities 1.0 g/cm³ and 1.45 g/cm³ (or, at least, does not decrease). For 0.01 M background, the equilibrium concentration instead falls quite dramatically between between densities 0.3 g/cm³ and 0.7 g/cm³, and thereafter displays only a minor density dependence.

To accept such dependencies, I require a considerably more rigorous experimental procedure and evaluation. In this case, I rather view the above plot as a confirmation of large uncertainties in parameter evaluation and sample properties.

• Chloride content: UNKNOWN
• Extracting anion equilibrium concentrations from through-diffusion tests
• Assessment of chloride equilibrium concentrations: Muurinen et al. (1988)

Footnotes

[1] Strictly, \(c(0,t)\) relates to the concentration in the endpoint of the inlet filter. But we ignore filter resistance in this assessment, which is valid for the 1.6/0.1 sample. Moreover, the filter diffusivities are not reported in Mo03.

[2] Mo03 refer to interlayer pores as “intralayer” pores, which may cause some confusion.

[3] Apparently, the authors assume an underlying stack view of the material.

[4] It may be objected that the analytical solution do not include the filter resistance. But note that filter resistance only will increase the delay. Moreover, the transport capacity of the sample in this test is so low that filters have no significant influence.

[5] The model by Mo03 looks noisy because I have read off values of accumulated concentration from the published graph. The “noise” occurs because the flux is evaluated from the concentration data by the difference formula:

\begin{equation} \bar{j}(\bar{t}_i) =\frac{1}{A} \frac{a(t_{i+1})-a(t_i)}{t_{i+1}-t_{i}} \end{equation}

where \(t_i\) and \(t_{i+1}\) are the time coordinates for two consequitive data points, \(a(t)\) is the accumulated amount diffused substance at time \(t\), \(A\) is the cross sectional area of the sample, \(\bar{t}_i = (t_{i+1} + t_i)/2\) is the average time of the considered time interval, and \(\bar{j}\) denotes the average flux during this time interval.

In the ongoing assessment of chloride equilibrium concentrations in bentonite, we here take a closer look at the study by Muurinen et al. (1988), in the following referred to as Mu88.¹ In the quite messy plot containing all reported chloride equilibrium concentrations, we thus investigate the twelve points indicated here

Mu88 performed both chloride and uranium through-diffusion tests on “MX-80” bentonite, as well as sorption tests. Here we focus solely on the chloride diffusion. We also disregard one diffusion test series that does not vary external concentration (it was conducted with an unspecified “artificial groundwater” and varied sample density).

Left are two test series performed with nominal sample densities 1.2 g/cm³ and 1.8 g/cm³, respectively. For each of these densities, chloride through-diffusion tests were performed with external NaCl concentrations of 0.01 M, 0.1 M, and 1.0 M, respectively. The samples were cylindrical with a diameter of 3.0 cm, and a length of 1.5 cm, giving a volume of 10.6 cm³. To refer to a specific test or sample, we use the nomenclature “nominal density/external concentration”, e.g. the test performed at nominal density 1.2 g/cm³ and external solution 0.1 M is referred to as “1.2/0.1”.

Uncertainty of bentonite samples

“MX-80” is not the name of some specific standardized material, but simply a product name.² It is quite peculiar that that “MX-80” nevertheless is a de facto standard in the research field for clay buffers in radwaste repositories. But, being a de facto standard, several batches of bentonite with this name have been investigated and reported throughout the years. We consequently have some appreciation for its constitution, and the associated variation.

In Mu88, the material used is only mentioned by name, and it is only mentioned once (in the abstract!). We therefore can’t tell which of the studies that is more appropriate to refer to. Instead, let’s take a look at how “MX-80” has been reported generally.

Report	Batch year	Mmt content	CEC	Na-content
		(%)	(eq/kg)	(%)
TR-06-30 (“WySt”)	1980	82.5	0.76	83
NTR 83-12	< 1983	75.5	0.76	86
TR-06-30 (“WyL1”)	1995	79.5	0.77	–
TR-06-30 (“WyL2”)	1999	79.8	0.75	71
TR-06-30 (“WyR1”)	2001	82.7	0.75	75
TR-06-30 (“WyR2”)	2001	80.0	0.71	71
NTB 01-08	< 2002	–	0.79*	85
WR 2004-023	< 2004	80 — 85	0.84*	65

Montmorillonite content

Reported montmorillonite content varies in the range 75 — 85%. For the present context, this primarily gives an uncertainty in adopted effective montmorillonite dry density, which, in turn, is important for making relevant comparison between bentonite materials with different montmorillonite content. For the “MX-80” used in Mu88 we here assume a montmorillonite content of 80%. In the table below is listed the corresponding effective montmorillonite densities when varying the montmorillonite content in the range \(x =\) 0.75 — 0.85, for the two nominal dry densities.

Dry density	EMDD (\(x\)=0.75)	EMDD (\(x\)=0.80)	EMDD (\(x\)=0.85)
(g/cm3)	(g/cm3)	(g/cm3)	(g/cm3)
1.2	1.01	1.05	1.09
1.8	1.61	1.66	1.70

The uncertainty in montmorillonite content thus translates to an uncertainty in effective montmorillonite dry density on the order of 0.1 g/cm³.

Cation population

While reported values of the cation exchange capacity of “MX-80” are relatively constant, of around 0.75 eq/kg,⁴ the reported fraction of sodium ions is seen to vary, in the range 70 — 85 %. The remaining population is mainly di-valent rare-earth metal ions (calcium and magnesium). This does not only mean that different studies on “MX-80” may give results for quite different types of systems, as the mono- to di-valent ion ratio may vary, but also that samples within the study may represent quite different systems. We examine this uncertainty below, when discussing the external solutions.

Soluble calcium minerals

The uncertainty of how much divalent cations are available is in fact larger than just discussed. “MX-80” is reported to contain a certain amount of soluble calcium minerals, in particular gypsum. These provide additional sources for divalent ions, which certainly will be involved in the chemical equilibration as the samples are water saturated. Reported values of gypsum content in “MX-80” are on the order of 1%. With a molar mass of 0.172 kg/mol, this contributes to the calcium content by \(2\cdot 0.01/0.172\) eq/kg \(\approx 0.12\) eq/kg, or about 16% of the cation exchange capacity.

Sample density

The samples in Mu88 that we focus on have nominal dry density of 1.2 and 1.8 g/cm³. The paper also reports measured porosities on each individual sample, listed in the below table together with corresponding values of dry density⁵

Test	\(\phi\)	\(\rho_d\)
	(-)	(g/cm3)
1.2/0.01	0.54	1.27
1.2/0.1	0.52	1.32
1.2/1.0	0.49	1.40
1.8/0.01	0.37	1.73
1.8/0.1	0.31	1.89
1.8/1.0	0.34	1.81

We note a substantial variation in measured density for samples with the same nominal density: for the 1.2 g/cm³ samples, the standard deviation is 0.06 g/cm³, and for the 1.8 g/cm³ samples it is 0.07 g/cm³. Moreover, while the mean value for the 1.8 g/cm³ samples is close to the nominal value (1.81 g/cm³), that for the 1.2 g/cm³ samples is substantially higher (1.33 g/cm³).

It is impossible to know from the information provided in Mu88 if this uncertainty is intrinsic to the procedure of preparing the samples, or if it is more related to the procedure of measuring the density at test termination.⁶

Uncertainty of external solutions

Mu88 do not describe how the external solutions were prepared. We assume here, however, that preparing pure NaCl solutions gives no significant uncertainty.

Further, the paper contains no information on how the samples were water saturated, nor on the external solution volumes. Since samples with an appreciable amount of di-valent cations are contacted with pure sodium solutions, it is unavoidable that an ion exchange process is initiated. As we don’t know any detail of the preparation process, this introduces an uncertainty of the exact aqueous chemistry during the course of a test.

To illustrate this problem, here are the results from calculating the exchange equilibrium between a sample initially containing 30% exchangeable charge in form of calcium (70% sodium), and external NaCl solutions of various concentrations and volumes

In these calculations we assume a sample of density 1.8 g/cm³ with the same volume as in Mu88 (10.6 cm³), a cation exchange capacity of 0.75 eq/kg, and a Ca/Na selectivity coefficient of 5.

In a main series, we varied the external volume between 50 and 1000 ml (solid lines). While the solution volume naturally has a significant influence on the process, it is seen that the initial calcium content essentially remain for the lowest concentration (0.01 M). In contrast, for a 1.0 M solution, a significant amount of calcium is exchanged for all the solution volumes.

The figure also shows a case for sample density 1.2 g/cm³ (dashed line), and a scenario where equilibrium has been obtained twice, with a replacement of the first solution (to a once again pure NaCl solution) (dot-dashed line).

The main lesson from these simulations is that the actual amount of di-valent ions present during a diffusion test depends on many details: the way samples were saturated, volume of external solutions, if and how often solutions were replaced, time, etc. It is therefore impossible to state the exact ion population in any of the tests in Mu88. But, guided by the simulations, it seems very probable that the tests performed at 0.01 M contain a substantial amount of di-valent ions, while those performed at 1.0 M probably resemble more pure sodium systems.

The only information on external solutions in Mu88 is that the “solution on the low concentration side was changed regularly” during the course of a test. This implies that the amount of di-valent cations may not even be constant during the tests.

Uncertainty of diffusion parameters

The diffusion parameters explicitly listed in Mu88 are \(D_e\) and “\(D_a\)”, while it is implicitly understood that they have been obtained by fitting the effective porosity model to outflux data and the measured clay concentration profile in the final state. “\(D_a\)” is thus really the pore diffusivity \(D_p\),⁷ and relates to \(D_e\) as \(D_e = \epsilon_\mathrm{eff} D_p\), where \(\epsilon_\mathrm{eff}\) is the so-called “effective porosity”. In a previous blog post, we discussed in detail how anion equilibrium concentrations can be extracted from through-diffusion tests, and the results derived there is used extensively in this section.

Rather than fitting the model to the full set of data (i.e. outflux evolution and final state concentration profile), diffusion parameters in Mu88 have been extracted in various limits.

Evaluation of \(D_e\) in Mu88

The effective diffusivity was obtained by estimating the steady-state flux, dividing by external concentration difference of the tracer, and multiplying by sample length \begin{equation} D_e = \frac{j^\mathrm{ss}\cdot L}{c^\mathrm{source}}\tag{1} \end{equation}

Here it is assumed that the target reservoir tracer concentration can be neglected (we assume this throughout). Eq. 1 is basically eq. 1 in Mu88 (and eq. 8 in the earlier blog post), from which we can evaluate the values of the steady-state flux that was used for the reported values of \(D_e\) (\(A \approx 7.1\) cm² denotes sample cross sectional area)

Test	\(D_e\)	\(A\cdot j^\mathrm{ss}/c^\mathrm{source}\)
	(\(\mathrm{m^2/s}\))	(ml/day)
1.2/0.01	\(7.7\cdot 10^{-12}\)	0.031
1.2/0.1	\(2.9\cdot 10^{-11}\)	0.118
1.2/1.0	\(1.2\cdot 10^{-10}\)	0.489
1.8/0.01	\(3.3\cdot 10^{-13}\)	0.001
1.8/0.1	\(4.8\cdot 10^{-13}\)	0.002
1.8/1.0	\(4.0\cdot 10^{-12}\)	0.016

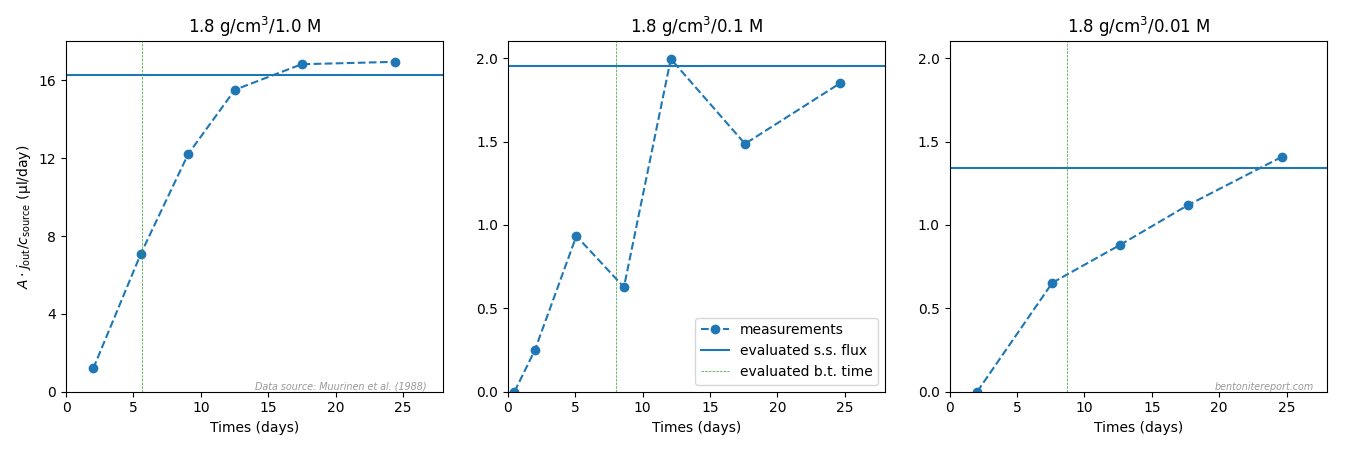
The figure below compares the evaluated values of the steady-state flux with the flux evaluated from the measured target concentration evolution,⁸ for samples with nominal dry density 1.8 g/cm³ (no concentration data was reported for the 1.2 g/cm³ samples)

These plots clearly show that the transition to steady-state is only resolved properly for the test with highest background concentration (1.0 M). It follows that the uncertainty of the evaluated steady-state — and, consequently, of the evaluated \(D_e\) values — increases dramatically with decreasing background concentration for these samples.

Evaluation of \(D_p\) in Mu88

Pore diffusivities were obtained in two different ways. One method was to relate the steady-state flux to the clay concentration profile at the end of the test, giving \begin{equation} D_{p,c} = \frac{j^\mathrm{ss}\cdot L}{\phi\cdot\bar{c}(0)} \tag{2} \end{equation}

where \(\bar{c}(0)\) denotes the chloride clay concentration at the interface to the source reservoir. The quantity in eq. 2 is called “\(D_{ac}\)”⁷ in Mu88, and this equation is essentially the same as eq. 2 in Mu88⁹ (and eq. 10 in the previous blog post). Using the steady-state fluxes, we can back-calculate the values of \(\bar{c}(0)\) used for this evaluation of \(D_{p,c}\)

Test	\(D_{p,c}\)	\(A\cdot j^\mathrm{ss}/c^\mathrm{source}\)	\(\phi\)	\(\bar{c}(0)/c^\mathrm{source}\)
	(\(\mathrm{m^2/s}\))	(ml/day)	(-)	(-)
1.2/0.01	\(7.0\cdot 10^{-11}\)	0.031	0.54	0.204
1.2/0.1	\(2.8\cdot 10^{-10}\)	0.118	0.52	0.199
1.2/1.0	\(5.1\cdot 10^{-10}\)	0.489	0.49	0.480
1.8/0.01	\(2.0\cdot 10^{-11}\)	0.001	0.37	0.045
1.8/0.1	\(3.1\cdot 10^{-11}\)	0.002	0.31	0.050
1.8/1.0	\(5.2\cdot 10^{-11}\)	0.016	0.34	0.226

Note that, although we did some calculations to obtain them, the values for \(\bar{c}(0)/c^\mathrm{source}\) in this table are closer to the actual measured raw data (concentrations). We made the calculation above to “de-derive” these values from the reported diffusion coefficients (combining eqs. 1 and 2 shows that \(\bar{c}(0)\) is obtained from the reported parameters as \(\bar{c}(0)/c^\mathrm{source} = D_e/(\phi D_{p,c})\)).

Here are compared the measured concentration profiles for the samples of nominal density 1.8 g/cm³ and the corresponding slopes used to evaluate \(D_{p,c}\) (profiles for the 1.2 g/cm³ samples are not provided in Mu88)

For background concentrations 1.0 M and 0.1 M, the evaluated slope corresponds quite well to the raw data. For the 0.01 M sample, however, the match is not very satisfactory. I suspect that a detection limit may have been reached for the analysis of the profile of this sample. Needless to say, the evaluated value of \(\bar{c}(0)\) is very uncertain for the 0.01 M sample.

It may also be noted that all measured concentration profiles deviates from linearity near the interface to the source reservoir. This is a general behavior in through-diffusion tests, which I am quite convinced of is related to sample swelling during dismantling, but there are also other suggested explanations. Here we neglect this effect and relate diffusion quantities to the linear parts of profiles, but this issue should certainly be treated in a separate discussion. Update (220407): non-linear profiles are discussed here.

\(D_p\) was also evaluated in a different way in Mu88, by measuring what we here will call the breakthrough time, \(t_\mathrm{bt}\) (Mu88 call it “time-lag”). This quantity is fairly abstract, and relates to the asymptotic behavior of the analytical expression for the outflux that apply for constant boundary concentrations (we here assume them to be \(c^\mathrm{source}\) and 0, respectively). This expression is displayed in eq. 7 in the previous blog post.

Multiplying the outflux by the sample cross sectional area \(A\) and integrating, gives the accumulated amount of diffused tracers. In the limit of long times, this quantity is, not surprisingly, linear in \(t\) \begin{equation} A\cdot j^\mathrm{ss} \cdot \left(t – \frac{L^2}{6\cdot D_p} \right ) \end{equation}

\(t_\mathrm{bt}\) is defined as the time for which this asymptotic expression is zero. Determining \(t_\mathrm{bt}\) from the measured outflux evolution consequently allows for an estimation of \(D_p\) as \begin{equation} D_{p,t} = \frac{L^2}{6t_\mathrm{bt}} \tag{3} \end{equation}

This quantity is called “\(D_{at}\)” in Mu88⁷ (eq. 3 is eq. 3 in Mu88). With another back calculation we can extract the values of \(t_\mathrm{bt}\) determined from the raw data

Test	\(D_{p,t}\)	\(t_\mathrm{bt}\)
	(\(\mathrm{m^2/s}\))	(days)
1.2/0.01	\(1.4\cdot 10^{-10}\)	3.1
1.2/0.1	\(2.0\cdot 10^{-10}\)	2.2
1.2/1.0	\(3.2\cdot 10^{-10}\)	1.4
1.8/0.01	\(5.0\cdot 10^{-11}\)	8.7
1.8/0.1	\(5.4\cdot 10^{-11}\)	8.0
1.8/1.0	\(7.7\cdot 10^{-11}\)	5.6

These evaluated breakthrough times are indicated in the flux plots above for samples of nominal dry density 1.8 g/cm³. For the 0.1 M and 0.01 M samples it is obvious that this value is very uncertain — without a certain steady-state flux it is impossible to achieve a certain breakthrough time. The breakthrough time for the 1.8/1.0 test, on the other hand, simply appears to be incorrectly evaluated: in terms of outflux vs. time, the breakthrough time should be the time where the flux has reached 62% of the steady-state value.¹⁰

As no raw data is reported for the 1.2 g/cm³ tests, the quality of the evaluated breakthrough times cannot be checked for them. It may be noted, however, that the evaluated breakthrough times are significantly shorter in this case as compared with the 1.8 g/cm³ tests. Consequently, while the sampling frequency is high enough to properly resolve the transient stage of the outflux evolution for the 1.8g/cm³ tests, it must be substantially higher in order to resolve this stage in the 1.2g/cm³ tests (I guess a rule of thumb is that sampling frequency must be at least higher than \(1/t_{bt}\)).

With the pore diffusivities evaluated from \(t_\mathrm{bt}\) we get a second estimation of \(\bar{c}(0)/c^\mathrm{source}\), using eq. 2. These values are listed in the table below and compared with the direct evaluation from the steady-state concentration profiles.

Test	\(\bar{c}(0)/c^\mathrm{source}\)	\(\bar{c}(0)/c^\mathrm{source}\)
	(breakthrough)	(profile)
1.2/0.01	0.102	0.204
1.2/0.1	0.279	0.199
1.2/1.0	0.765	0.480
1.8/0.01	0.018	0.045
1.8/0.1	0.029	0.050
1.8/1.0	0.153	0.226

In a well conducted study these estimates should be similar; \(D_{p,c}\) and \(D_{p,t}\) are, after all, estimations of the same quantity: the pore diffusivity \(D_p\).⁷ But here we note a discrepancy of approximately a factor 2 between several values of \(\bar{c}(0)\).

It is difficult to judge generally which of the estimations are more accurate, but we have seen that for the 1.8/0.1 and 1.8/0.01 tests, the flux data is not very well resolved, giving a corresponding uncertainty on the equilibrium concentration estimated from the breakthrough time. On the other hand, also the concentration profile is poorly resolved in the case of 0.01 M at 1.8 g/cm³.

However, in cases where the value of \(\bar{c}(0)/c^\mathrm{source}\) is substantial (as for the 1.8/1.0 test and, reasonably, for all tests at 1.2 g/cm³), we expect the estimation directly from the concentration profile to be accurate and robust (as for the 1.8 g/cm³ test at high NaCl concentration). For the 1.2 g/cm³ samples we cannot say much more than this, since Mu88 don’t provide the concentration raw data. For the 1.8/1.0 test, however, we can continue the analysis by fitting the model to all available data.

Re-evaluation by fitting to the full data set

Note that all evaluations in Mu88 are based on making an initial estimation of the steady-state flux, giving \(D_e\) (eq. 1). This value of \(D_e\) (or \(j^{ss}\)) is thereafter fixed in the subsequent estimation of \(D_{p,c}\) (eq. 2). Likewise, an estimation of the steady-state flux is required for estimating the breakthrough time. Here is an animation showing the variation of the model when transitioning from the value of the pore diffusivity estimated from breakthrough time (\(7.7\cdot 10^{-11}\) m²/s), to the value estimated from concentration profile (\(5.2\cdot 10^{-11}\) m²/s) for the 1.8/1.0 test, keeping the steady-state flux fixed at the initial estimation

Note that the axes for the flux is on top (time) and to the right (accumulation rate). This animation confirms that the diffusivity evaluated from breakthrough time in Mu88 gives a way too fast process: the slope of the steady-state concentration profile is too small, and the outflux evolution has a too short transient stage. On the other hand, using the diffusivity estimated from the concentration profiles still doesn’t give a flux that fit very well. The problem is that this fitting is performed with a fixed value of the steady-state flux. By instead keeping the slope fixed at the experimental values, while varying diffusivity (and thus steady state flux), we get the following variation

This animation shows that the model can be fitted well to all data (at least for the 1.8/1.0 test). The problem with the evaluation in Mu88 is that it assumes the steady-state to be fully reached at the later stages of the test. As the above fitting procedure shows, this is only barely true. The experiments could thus have been designed better by conducting them longer, in order to better sample the steady-state phase (and the steady-state flux should have been fitted to the entire data set). Nevertheless, for this sample, the steady-state flux obtained by allowing for this parameter to vary is only slightly different from that used in Mu88 (17.5 rather than 16.3 \(\mathrm{\mu}\)l/day, corresponding to a change of \(D_p\) from \(5.2\cdot10^{-11}\) to \(5.6\cdot10^{-11}\) m²/s). Moreover, this consideration should not be a problem for the 1.2 g/cm³ tests, if they were conducted for as long time as the 1.8 g/cm³ tests, because steady-state is reached much faster (in those tests, sampling frequency may instead be a problem, as discussed above).

As we were able to fit the full model to all data, we conclude that the value of \(\bar{c}(0)/c^\mathrm{source}\) obtained from \(D_{p,c}\) is probably the more robust estimation¹¹, and that there appears to be a problem with how the breakthrough times have been determined. For the 1.8 g/cm³ samples we have demonstrated that this is the case, for the 1.2 g/cm³ we can only make an educated guess that this is the case.

Summary and verdict

We have seen that the results on chloride diffusion in Mu88 suffer from uncertainty from several sources:

• The “MX-80” material is not that well defined
• Densities vary substantially for samples at the same nominal density
• Without knowledge of e.g water saturation procedures and solution volumes, it is impossible to estimate the proper ion population during the course of a test
• It is, however, highly likely that tests performed at low NaCl concentrations contain substantial amounts of di-valent ions, while those at high NaCl concentration are closer to being pure sodium systems.
• The reported diffusivities give a corresponding uncertainty in the chloride equilibrium concentrations of about a factor of 2. While some tests essentially have a too high noise level to give certain estimations, the problem for the others seems to stem from the estimation of breakthrough times.

Here is an attempt to encapsulate the above information in an updated plot for the chloride equilibrium data in Mu88

The colored squares represent “confidence areas” based on the variation within each nominal density (horizontally), and on the variation of \(\bar{c}(0)/c^\mathrm{source}\) from the two reported values on pore diffusivity⁷ (vertically). The limits of these rectangles are simply the 95% confidence interval, based on these variations, and assuming a normal distribution.

Data points put within parentheses are estimations judged to be improper (based on either re-evaluation of the raw data, or informed guesses).

From the present analysis my decision is to not use the data from Mu88 to e.g. validate models for anion exclusion. Although there seems to be nothing fundamentally wrong with how these test were conducted, they suffer from so many uncertainties of various sources that I judge the data to not contribute to quantitative process understanding.

• Chloride content: UNKNOWN
• Extracting anion equilibrium concentrations from through-diffusion tests
  

Footnotes

[1] This work is referred to as “Muurinen et al. (1989)” by several authors.

[2] MX-80 is not only a brand name, but also a band name.

[3] This report is “Bentonite Mineralogy” by L. Carlson (Posiva WR 2004-02), but it appears to not be included in the INIS database. It can, however, be found with some elementary web searching.

[4] It’s interesting to note that the cation exchange capacity of “MX-80” remains more or less constant, while the montmorillonite content has some variation. This implies that the montmorillonite layer charge varies (and is negatively correlated with montmorillonite content). Could it be that the manufacturer has a specified cation exchange capacity as requirement for this product?

[5] To convert porosity to dry density, I used \(\rho_d = \rho_s\cdot(1-\phi)\), with solid grain density \(\rho_s = 2.75\) g/cm³.

[6] A speculation is that the uncertainty stems from the measurement procedure, as this was done on smaller sections of the full samples. It is not specified in Mu88 what the reported porosity represent, but it is reasonable to assume that it is the average of all sections of a sample.

[7] At the risk of losing some clarity, I refuse to use the term “apparent diffusivity” for something which actually is a real pore diffusivity.

[8] These values were not tabulated, but I have read them off from the graphs in Mu88.

[9] Mu88 use the concentration based on the total volume in their expression, while \(\bar{c}\) is defined in terms of water volume (water mass, strictly). Eq.2 therefore contains the physical porosity. In their concentration profile plots, however, Mu88 use \(\bar{c}\) as variable (called \(c_{pw}\) — the “concentration in the pore water”)

[10] Plugging the breakthrough time \(L^2/6D_p\) into the expression for the flux gives

\begin{equation} j^\mathrm{out}(t_\mathrm{bt}) = j^{ss}\cdot\left ( 1 + 2 \sum (-1)^n e^\frac{-\pi^2 n^2}{6} \right ) \approx 0.616725\cdot j^{ss} \end{equation}

I find it amusing that this value is close to the reciprocal golden ratio (0.618033…). Finding the breakthrough time from a flux vs. time plot thus corresponds (approximately) to splitting the y-axis according to the golden ratio.

[11] Note that the actual evaluated values of $D_{p,c}$ in Mu88 still may be uncertain, because they also depend on the values of the steady-state flux, which we have seen were not optimally evaluated.