Category Archives: Thermodynamics

Solving the Poisson-Boltzmann equation

To celebrate that I have built myself a tool for solving the Poisson-Boltzmann equation for two parallel charged plates and specified external solution, here is a cosy little animation

The animation shows the anion concentration profile (blue) between the plates as the distance varies, in systems in equilibrium with an external 100 mM 1:1 salt solution. Also plotted is the corresponding internal concentration level as calculated from the ideal Donnan equilibrium formula (orange). The layer charge density in the Poisson-Boltzmann calculation is 0.111 C/m², and the corresponding cation exchange capacity in the Donnan calculation is 0.891 eq/kg.

As the distance between the plates increases, the Poisson-Boltzmann profile increasingly deviates from the Donnan concentration. At lower density (larger plate distance) it is clear that the Poisson-Boltzmann solution allows for considerably more anions between the plates as compared with the Donnan result. On the other hand, for denser systems, the difference between the two solutions decreases; this is especially true when considering the relative difference — keep in mind that the external concentration is kept constant, at 100 mM.

In fact, in systems relevant for e.g. radioactive waste storage — spanning an effective montmorillonite density range from \(\rho_\mathrm{mmt} =\) 1.60 g/cm³ to \(\rho_\mathrm{mmt} =\) 1.15 g/cm³, say — the difference between the Poisson-Boltzmann and the Donnan results is virtually negligible (it should also be kept in mind that the continuum assumption underlying the Poisson-Boltzmann calculation is not valid in this density range). Here are plotted snapshots of these two limiting cases, together with the Poisson-Boltzmann solution for a single plate (the Gouy-Chapman model)

This figure clearly shows that the Gouy-Chapman model is not at all valid in any relevant system, unless you postulate larger voids in the bentonite. But why would you do that?

Kahr et al. (1985) — the diffusion study that could have changed everything

Leave a reply

On the surface, “Ionendiffusion in Hochverdichtetem Bentonit”¹ by G. Kahr, R. Hasenpatt, and M. Müller-Vonmoos, published by NAGRA in March 1985, looks like an ordinary mundane 37-page technical report. But it contains experimental results that could have completely changed the history of model development for compacted clay.

Test principles

The tests were conducted in a quite original manner. By compacting granules or powder, the investigators obtained samples that schematically look like this

Schematics of samples in Kahr et al. (1985(

The bentonite material — which was either Na-dominated “MX-80”, or Ca-dominated “Montigel” — was conditioned to a specific water-to-solid mass ratio \(w\). At one of the faces, the bentonite was mixed with a salt (in solid form) to form a thin source for diffusing ions. This is essentially the full test set-up! Diffusion begins as soon as the samples are prepared, and a test was terminated after some prescribed amount of time, depending on diffusing ion and water content. At termination, the samples were sectioned and analyzed. In this way, the investigators obtained final state ion distributions, which in turn were related to the initial states by a model, giving the diffusion coefficients of interest.

Note that the experiments were conducted without exposing samples to a liquid (external) solution; the samples were “unsaturated” to various degree, and the diffusing ions dissolve within the bentonite. The samples were not even confined in a test cell, but “free-standing”, and consequently not under pressure. They were, however, stored in closed vessels during the course of the tests, to avoid changes in water content.

With this test principle a huge set of diffusion tests were performed, with systematic variation of the following variables:

Bentonite material (“MX-80” or “Montigel”)
Water-to-solid mass ratio (7% — 33%)
Dry density (1.3 g/m³ — 2.1 g/m³ )
Diffusing salt (SrCl₂, SrI₂, CsCl, CsI, UO₂(NO₃)₂, Th(NO₃)₄, KCl, KI, KNO₃, K₂SO₄, K₂CO₃, KF)

Distribution of water in the samples

From e.g. X-ray diffraction (XRD) we know that bentonite water at low water content is distributed in distinct, sub-nm thin films. For simplicity we will refer to all water in the samples as interlayer water, although some of it, reasonably, forms interfaces with air. The relevant point is that the samples contain no bulk water phase, but only interfacial (interlayer) water.

I argue extensively on this blog for that interlayer water is the only relevant water phase also in saturated samples under pressure. In the present case, however, it is easier to prove that this is the case, as the samples are merely pressed bentonite powder at a certain water content; the bentonite water is not pressurized, the samples are not exposed to liquid bulk water, nor are they in equilibrium with liquid bulk water. Since the water in the samples obviously is mobile — as vapor, but most reasonably also in interconnected interlayers — it is a thermodynamic consequence that it distributes as to minimize the chemical potential.

There is a ton of literature on how the montmorillonite basal spacing varies with water content. Here, we use the neat result from Holmboe et al. (2012) that the average interlayer distance varies basically linearly² with water content, like this

average basal distance vs. water content from Holmboe et al. (2012)

XRD-studies also show that bentonite water is distributed in rather distinct hydration states, corresponding to 0, 1, 2, or 3 monolayers of water.³ We label these states 0WL, 1WL, 2WL, and 3WL, respectively. In the figure is indicated the approximate basal distances for pure 1WL (12.4 Å), 2WL (15.7 Å), and 3WL (19.0 Å), which correspond roughly to water-to-solid mass ratios of 0.1, 0.2, and 0.3, respectively.

From the above plot, we estimate roughly that the driest samples in Kahr et al. (1985) (\(w \sim 0.1\)) are in pure 1WL states, then transitions to a mixture of 1WL and 2WL states (\(w\sim 0.1 – 0.2\)), to pure 2WL states (\(w \sim 0.2\)), to a mixture of 2WL and 3WL states (\(w\sim 0.2 – 0.3\)), and finally to pure 3WL states (\(w\sim 0.3\)).

Results

With the knowledge of how water is distributed in the samples, let’s take a look at the results of Kahr et al. (1985).

Mobility of interlayer cations confirmed

The most remarkable results are of qualitative character. It is, for instance, demonstrated that several cations diffuse far into the samples. Since the samples only contain interlayer water, this is a direct proof of ion mobility in the interlayers!

Also, cations are demonstrated to be mobile even when the water content is as low as 7 or 10 %! As such samples are dominated by 1WL states, this is consequently evidence for ion mobility in 1WL states.

A more quantitative assessment furthermore shows that the cation diffusivities varies with water content in an almost step-wise manner, corresponding neatly to the transitions between various hydration states. Here is the data for potassium and strontium

De vs. water content for potassium and strontium from Kahr et al. (1985)

This behavior further confirms that the ions diffuse in interlayers, with an increasing diffusivity as the interlayers widen.

It should also be noted that the evaluated values of the diffusivities are comparable to — or even larger⁴ — than corresponding results from saturated, pressurized tests. This strongly suggests that interlayer diffusivity dominates also in the latter types of tests, which also has been confirmed in more recent years. The larger implication is that interlayer diffusion is the only relevant type of diffusion in general in compacted bentonite.

Anions enter interlayers (and are mobile)

The results also clearly demonstrate that anions (iodide) diffuse in systems with water-to-solid mass ratio as low as 7%! With no other water around, this demonstrates that anions diffuse in — and consequently have access to — interlayers. This finding is strongly confirmed by comparing the \(w\)-dependence of diffusivity for anions and cations. Here is plotted the data for iodide and potassium (with the potassium diffusivity indicated on the right y-axis)

De vs. water content for iodide and potassium from Kahr et al. (1985)

The iodide mobility increases as the system transitions from 1WL to 2WL, in a very similar way as for potassium (and strontium). If this is not a proof that the anion diffuse in the same domain as the cation I don’t know what is! Also for iodide the value of the diffusivity is comparable to what is evaluated in water saturated systems under pressure, which implies that interlayer diffusivity dominates generally in compacted bentonite, also for anions.

Dependence of diffusivity on water content and density

A conclusion made in Kahr et al. (1985), that I am not sure I fully agree with, is that diffusivity mainly depends on water content rather than density. As seen in the diagrams above, the spread in diffusivity is quite substantial for a given value of \(w\). There is actually some systematic variation here: for constant \(w\), diffusivity tend to increase with dry density.

Although using unsaturated samples introduces additional variation, the present study provides a convenient procedure to study diffusion in systems with very low water content. A more conventional set-up in this density limit has to deal with enormous pressures (on the order of 100 MPa).

Interlayer chemistry

An additional result is not acknowledged in the report, but is a direct consequence of the observations: the tests demonstrate that interlayers are chemically active. The initially solid salt evidently dissolves before being able to diffuse. Since these samples are not even close to containing a bulk water phase (as discussed above), the dissolution process must occur in an interlayer. More precisely, the salt must dissolve in interface water between the salt mineral and individual montmorillonite layers, as illustrated here

Schematics of KI dissolution in interlayer water

This study seems to have made no impact at all

In the beginning of 1985, the research community devoted to radioactive waste barriers seems to have been on its way to correctly identify diffusion in interlayers as the main transport mechanism, and to recognize how ion diffusion in bentonite is influenced by equilibrium with external solutions.

Already in 1981, Torstenfelt et al. (1981) concluded that the traditional diffusion-sorption model is not valid, for e.g. diffusion of Sr and Cs, in compacted bentonite. They also noted, seemingly without realizing the full importance, that these ions diffused even in unsaturated samples with as low water-to-solid mass ratio as 10%.

A significant diffusion was observed for Sr in dry clay, although slower than for water saturated clay, Figure 4, while Cs was almost immobile in the dry clay.

A year later also Eriksen and Jacobsson (1982) concluded that the traditional diffusion model is not valid. They furthermore pointed out the subtleties involved when interpreting through-diffusion experiments, due to ion equilibrium effects

One difficulty in correlating the diffusivities obtained from profile analysis to the diffusivities calculated from steady state transport data is the lack of knowledge of the tracer concentration at the solution-bentonite interface. This concentration is generally higher for sorbing species like positive ions (counterions to the bentonite) and lower for negative ions (coions to the bentonite) as shown schematically in figure 11. The equilibrium concentration of any ion in the bentonite and solution respectively is a function of the ionic charge, the ionic strength of the solution and the overall exchanger composition and thereby not readily calculated

In Eriksen and Jacobsson (1984) the picture is fully clear

By regarding the clay-gel as a concentrated electrolytic system Marinsky has calculated (30) distribution coefficients for Sr²⁺ and Cs⁺ ions in good agreement with experimentally determined K_d-values. The low anionic exchange capacity and hence the low anion concentration in the pore solution caused by Donnan exclusion also explain the low concentrations of anionic tracers within the clay-gel
[…]
For simple cations the ion-exchange process is dominating and there is, as also pointed out by Marinsky (30), no need to suppose that the counterions are immobilized. It ought to be emphasized that for the compacted bentonite used in the diffusion experiments discussed in this report the water content corresponds roughly to 2-4 water molecule layers (31). There is therefore really no “free water” and the measured diffusivity \(\bar{D}\) can be regarded as corresponding approximately to the diffusivity within the adsorbed phase […]

Furthermore, also Soudek et al. (1984) had discarded the traditional diffusion-sorption model, identified the exchangeable cations as giving a dominating contribution to mass transfer, and used Donnan equilibrium calculations to account for the suppressed internal chloride concentration.

In light of this state of the research front, the contribution of Kahr et al. (1985) cannot be described as anything but optimal. In contrast to basically all earlier studies, this work provides systematic variation of several variables (most notably, the water-to-solid ratio). As a consequence, the results provide a profound confirmation of the view described by Eriksen and Jacobsson (1984) above, i.e. that interlayer pores essentially govern all physico-chemical behavior in compacted bentonite. A similar description was later given by Bucher and Müller-Vonmoos (1989) (though I don’t agree with all the detailed statements here)

There is no free pore water in highly compacted bentonite. The water in the interlayer space of montmorillonite has properties that are quite different from those of free pore water; this explains the extremely high swelling pressures that are generated. The water molecules in the interlayer space are less mobile than their free counterparts, and their dielectric constant is lower. The water and the exchangeable cations in the interlayer space can be compared to a concentrated salt solution. The sodium content of the interlayer water, at a water content of 25%, corresponds approximately to a 3-n salt solution, or six times the concentration in natural seawater. This more or less ordered water is fundamentally different from that which engineers usually take into account; in the latter case, pore water in a saturated soil is considered as a freely flowing fluid. References to the porosity in highly compacted bentonite are therefore misleading. Highly compacted bentonite is an unfamiliar material to the engineer.

Given this state of the research field in the mid-80s, I find it remarkable that history took a different turn. It appears as the results of Kahr et al. (1985) made no impact at all (it may be noticed that they themselves analyzed the results in terms of the traditional diffusion-sorption model). And rather than that researchers began identifying that transport in interlayers is the only relevant contribution, the so-called surface diffusion model gained popularity (it was already promoted by e.g. Soudek et al. (1984) and Neretnieks and Rasmuson (1983)). Although this model emphasizes mobility of the exchangeable cations, it is still centered around the idea that compacted bentonite contains bulk water.⁵ Most modern bentonite models suffer from similar flaws: they are formulated in terms of bulk water, while many effects related to interlayers are treated as irrelevant or optional.

For the case of anion diffusion the historical evolution is maybe even more disheartening. In 1985 the notions of “effective” or “anion-accessible” porosities seem to not have been that widely spread, and here was clear-cut evidence of anions occupying interlayer pores. But just a few years later the idea began to grow that the pore space in compacted bentonite should be divided into regions which are either accessible or inaccessible to anions. As far as I am aware, the first use of the term “effective porosity” in this context was used by Muurinen et al. (1988), who, ironically, seem to have misinterpreted the Donnan equilibrium approach presented by Soudek et al. (1984). To this day, this flawed concept is central in many descriptions of compacted clay.

Footnotes

[1] “Ion diffusion in highly compacted bentonite”

[2] Incidentally, the slope of this line corresponds to a water “density” of 1.0 g/cm³.

[3] This is the region of swelling often referred to as “crystalline”.

[4] I’m not sure the evaluation in Kahr et al. (1985) is fully correct. They use the solution to the diffusion equation for an impulse source (a Gaussian), but, to my mind, the source is rather one of constant concentration (set by the solubility of the salt). Unless I have misunderstood, the mathematical expression to be fitted to data should then be an erfc-function, rather than a Gaussian. Although this modification would change the numerical values of the evaluated diffusion coefficients somewhat, it does not at all influence the qualitative insights provided by the study.

[5] I have discussed the surface diffusion model in some detail in previous blog posts.

The mechanism for “anion” exclusion

Leave a reply

Repulsion between surfaces and anions is not really the point

Many publications dealing with “anion” exclusion in compacted bentonite describe the phenomenon as being primarily due to electrostatic repulsion of anions from the negatively charged clay surfaces. This explanation, which may seem plausible both at a first and a second glance, is actually not that satisfactory. There are two major issues to consider:

Although it is popular to use the word “anion” when referring to the phenomenon, it must be remembered that the anions are accompanied by cations, in order to maintain overall charge neutrality; it really is salt that is excluded from the bentonite. This observation shows that the above “explanation” is incomplete: it can be argued with the same logic that salt should accumulate, because the clay surfaces attract the cations of the external salt.
Salt exclusion occurs generally in Donnan systems, also in those that lack surfaces. Its principal explanation can consequently not involve the presence of surfaces. For a simpler system, e.g. potassium ferrocyanide, the “explanation” above translates to claiming that exclusion is caused by “anions” being electrostatically repelled by the ferrocyanide ions. In this case it may be easier to spot the shortcoming of such a claim, and to consider also the potassium ions (which attract anions), as well as the role played by the cations of the excluded salt.

What, then, is the primary cause for salt exclusion? Let us continue with using potassium ferrocyanide as an example of a simple Donnan system, and then translate our findings to the case of compacted bentonite.

Ferrocyanide

Consider a potassium ferrocyanide solution separated from a potassium chloride solution by a membrane permeable to all but the ferrocyanide ions. The ionic configuration near the membrane then looks something like this

Because potassium ions can pass the membrane, and because they have an entropic driving force to migrate out of the ferrocyanide solution, a (microscopic) region is formed in the external solution next to the membrane, with an excess amount of positive charge. Similarly, a region is formed next to the membrane in the ferrocyanide solution with an excess amount of negative charge. Thus, a region of charge separation exists across the membrane — similar to the depletion zone in a p-n junction — over which the electrostatic potential varies. The electric field (= a varying potential) at the interface acts as to pull back potassium ions towards the ferrocyanide solution. The equilibrium width of the space charge region is set when the diffusive flux is balanced by the flux due to the electric field.

With a qualitative understanding of the electrostatic potential configuration we can now give the most plain answer to what causes “anion” exclusion: it is because of the potential difference across the membrane. Chloride ions behave in the opposite way as compared to potassium, with an entropic driving force to enter the ferrocyanide solution, while being pulled back towards the external solution due to the electric field across the membrane.

Here the mindful reader may perhaps object and point out that the electric field restricting the chloride inflow reasonably originates from the ferrocyanide anions. It thus may seem that “anion” exclusion, after all, is caused by repulsion from other negative charges.

Indeed, electrostatic repulsion of anions requires the “push” of some other negatively charged entity. But note that the potential is constant in the interior of the ferrocyanide solution, and only varies near the membrane. The variation of the potential is caused by separation of charge: chloride is as much “pushed” out of the ferrocyanide solution by the ferrocyanide as it is “pulled” out of it, due to electrostatic attraction, by the excess potassium on the other side. Repulsion between charges of equal sign occurs also in the interior of the ferrocyanide solution (or in any ionic solution), but does not in itself lead to salt exclusion.

Bentonite

The above description can be directly transferred to the case of compacted bentonite. Replacing the potassium ferrocyanide with e.g. K-montmorillonite, salt exclusion occurs mainly because potassium can migrate out of the clay region, while montmorillonite particles cannot. Again, we have charge separation with a resulting varying electrostatic potential across the interface.

Admittedly, the general situation is more complicated in bentonite because of the extension of montmorillonite particles; viewed as “anions”, these are irregularly shaped macromolecules with hundreds or thousands of charge centers.

The ion configuration in a bentonite suspension therefore looks quite different from a corresponding ordinary solution, as the montmorillonite charge obviously is constrained to individual particles. Dilute systems thus have charge separation on the particle scale and show salt exclusion even without charge separation at the interface to the external solution. These types of systems (suspensions) have historically been the subject of most studies on “anion” exclusion, and are usually treated theoretically using the Gouy-Chapman model.

With increasing density, however, the effect of a varying potential between montmorillonite particles diminishes, while the effect of charge separation at the interface increases. For dense systems (> 1.2 g/cm³, say), we may therefore approximate the internal potential as constant and only consider the variation across the interface to the external solution using Donnan’s “classical” framework.¹

Here is an illustration of the validity of this approximation:

Internal and external potential in compacted bentonite system

The figure shows the difference between the external (green) and the average internal (orange) potentials in a 1:1 system of density 1.3 g/cm³ and with external concentration 0.1 M, calculated using Donnan’s “classical” equation. Also plotted is the electrostatic potential across the interlayer (blue) as calculated using the Poisson-Boltzmann equation,² in a similar system (interlayer distance 1 nm). It is clear that the variation of the Poisson-Boltzmann potential from the average is small in comparison with the Donnan potential.

Repulsion between chloride and montmorillonite particles of course occurs everywhere in compacted bentonite, whereas the phenomenon mainly responsible for salt exclusion occurs only near the interfaces. Merely stating electrostatic repulsion as the cause for salt exclusion in compacted bentonite does not suffice, just as in the case of ferrocyanide.

To illustrate that the salt exclusion effect depends critically on exchangeable cations being able to diffuse out of the bentonite, consider the following thought experiment.³ Compacted K-montmorillonite is contacted with a NaCl solution. But rather than having a conventional component separating the solution and the clay, we imagine a membrane that does not allow for the passage of neither potassium nor clay, but that allows for the passage of sodium and chloride. Since potassium is not allowed to diffuse out of the bentonite, no charge separation occurs across the membrane. With no space charge region, the electrostatic potential does not vary and NaCl is not excluded! (to the extent that the Donnan approximation is valid)

NaCl + K-montmorillonite with interface only permeable for Na and Cl

A charge neutral perspective

The explanation for “anion” exclusion that we have explored rests on the formation of a potential difference across the interface region between bentonite and external solution. But remember that it is salt — in our example KCl — that is excluded from the bentonite (or the ferrocyanide solution), and that the cation (K) gains energy by being transferred from the external to the internal solution. The electrical work for transferring a unit of KCl is thus zero (which makes sense since KCl is a charge neutral entity). In this light, it may seem unsatisfactory to offer the potential difference as the sole explanation for salt exclusion.

I therefore think that the following kinematic way of reasoning is very helpful. Instead of considering the mass transfer of Cl across the membrane in terms of oppositely directed “electric” and “diffusive” parts, we lump them together with equal amounts of K transfer, giving two equal but oppositely directed fluxes of KCl. Reasonably, the KCl flux into the ferrocyanide solution is proportional to the external ion concentrations

\begin{equation} j^\mathrm{in}_\mathrm{KCl} = A\cdot c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} \end{equation}

while the outflux is proportional to the internal ion concentrations

\begin{equation} j^\mathrm{out}_\mathrm{KCl} = -A\cdot c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

\(A\) is a coefficient accounting for the transfer resistance across the interface region. Requiring the sum of these fluxes to be zero gives the following relation

\begin{equation} c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} = c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

which is the (ideal) Donnan equation.

We can therefore interpret KCl exclusion as an effect of potassium in the clay providing a potential for “out-transfer”, as soon as the chance is given, i.e. when chloride enters from the external solution. From this perspective salt exclusion could maybe be said to be a form of cation “rejection”.

Footnotes

[1] Note also that the Gouy-Chapman model is not valid in the high density limit, although it is applied (or alluded to) in this limit in many publications. But e.g. Schofield (1947) states (about the Gouy-Chapman solution):

[T]he equation is applicable to cases in which the distance between opposing surfaces considerably exceeds the distance between neighboring point charges on the surfaces; for there will then be a range of electrolyte concentrations over which the radius of the ionic atmosphere is less than the former and greater than the latter.

This criterion is not met in compacted bentonite, where instead the interlayer distance is comparable to the distance between neighboring charge centers on the surfaces. Invalid application of the Gouy-Chapman model also seems to underlie the flawed but widespread “anion-accessible porosity” concept.

[2] This calculation uses the equations presented in Engström and Wennerström (1978), and assumes no excess ions and a surface charge density of 0.111 \(\mathrm{C/m^2}\). For real consistency this calculation should really be performed with the boundary condition of 0.1 M external concentration. However, since the purpose of the graph is just to demonstrate the sizes of the two potential variations, and since I have yet to acquire a reasonable tool for performing Poisson-Boltzmann calculations with non-zero external concentration, I disregard this inconsistency. Moreover, the continuum assumption of the Poisson-Boltzmann description is anyway beginning to lose its validity at these interlayer distances. Update (220831): Solutions to the Poisson-Boltzmann equation with non-zero external concentration are presented here.

[3] Perhaps this could be done as a Molecular Dynamics simulation?

Swelling pressure, part V: Suction

Leave a reply

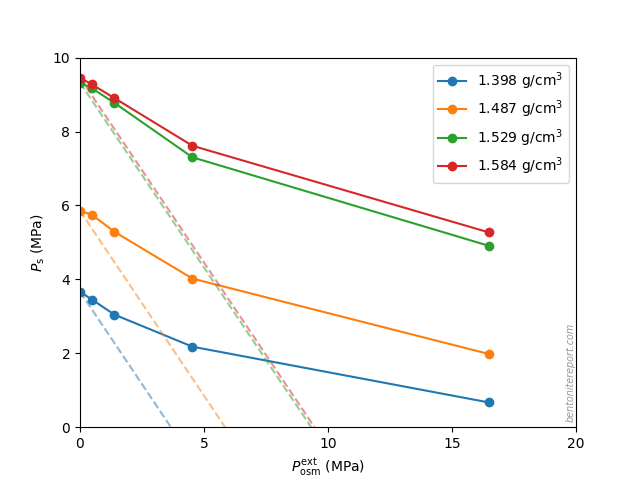
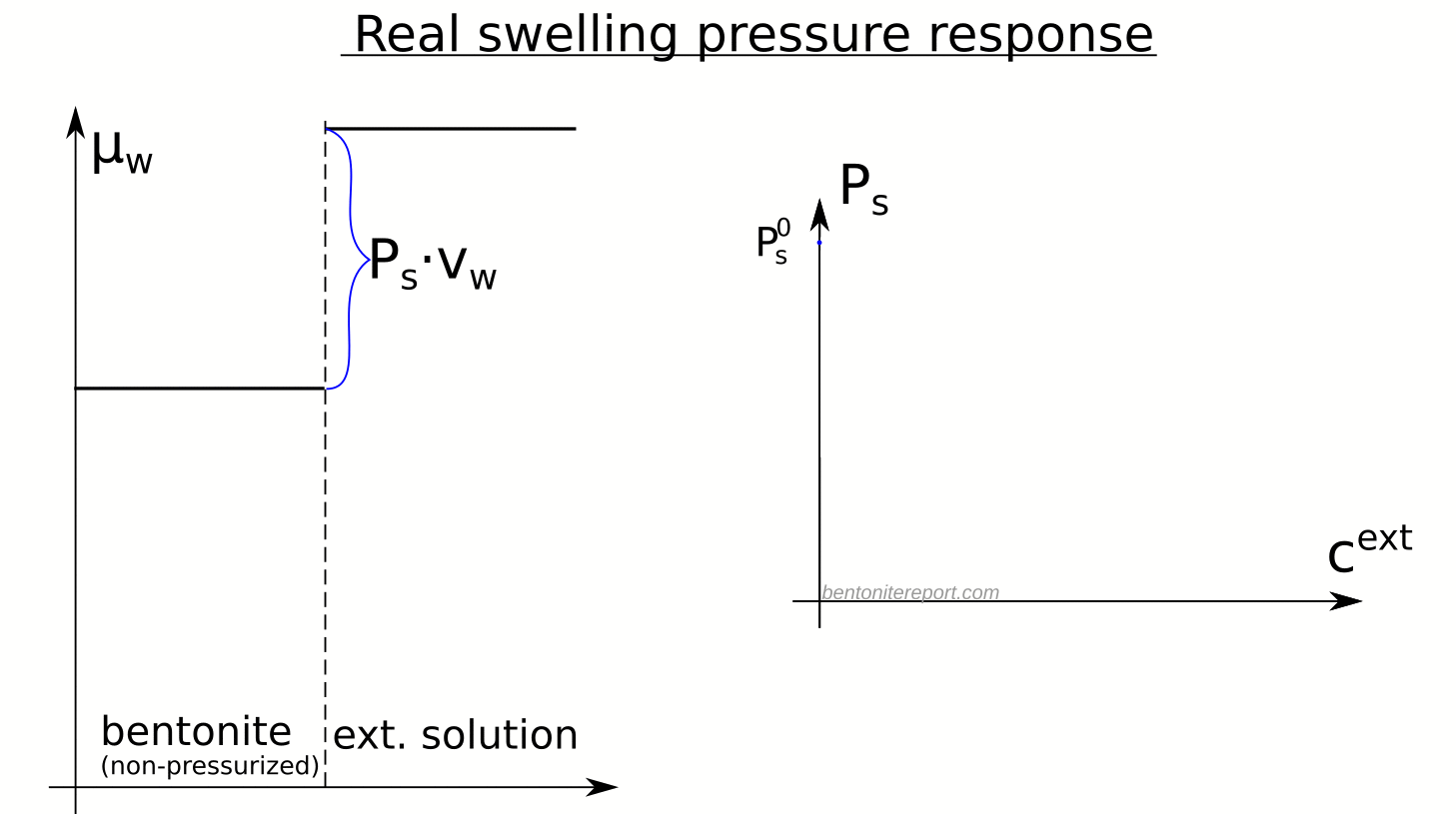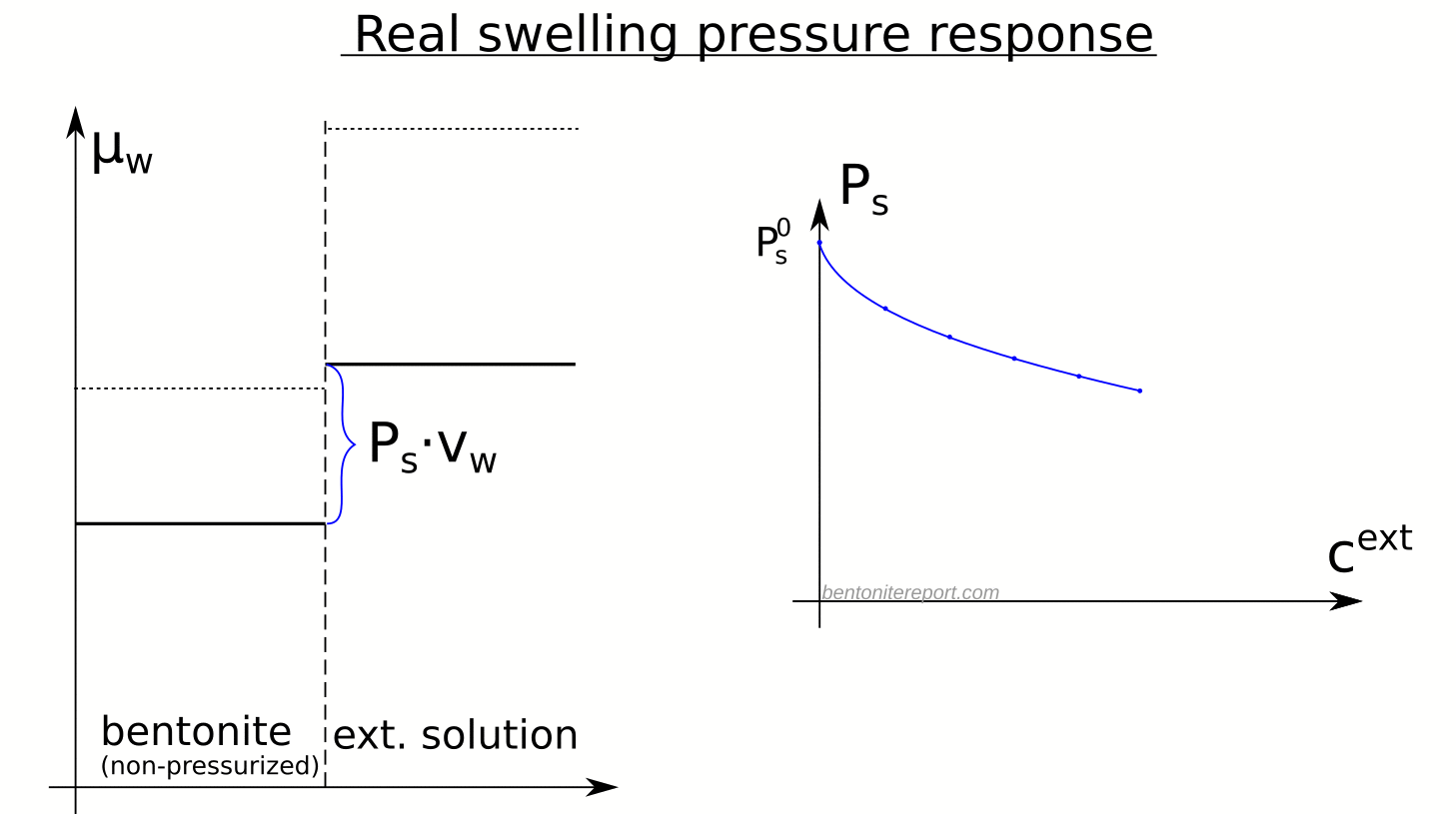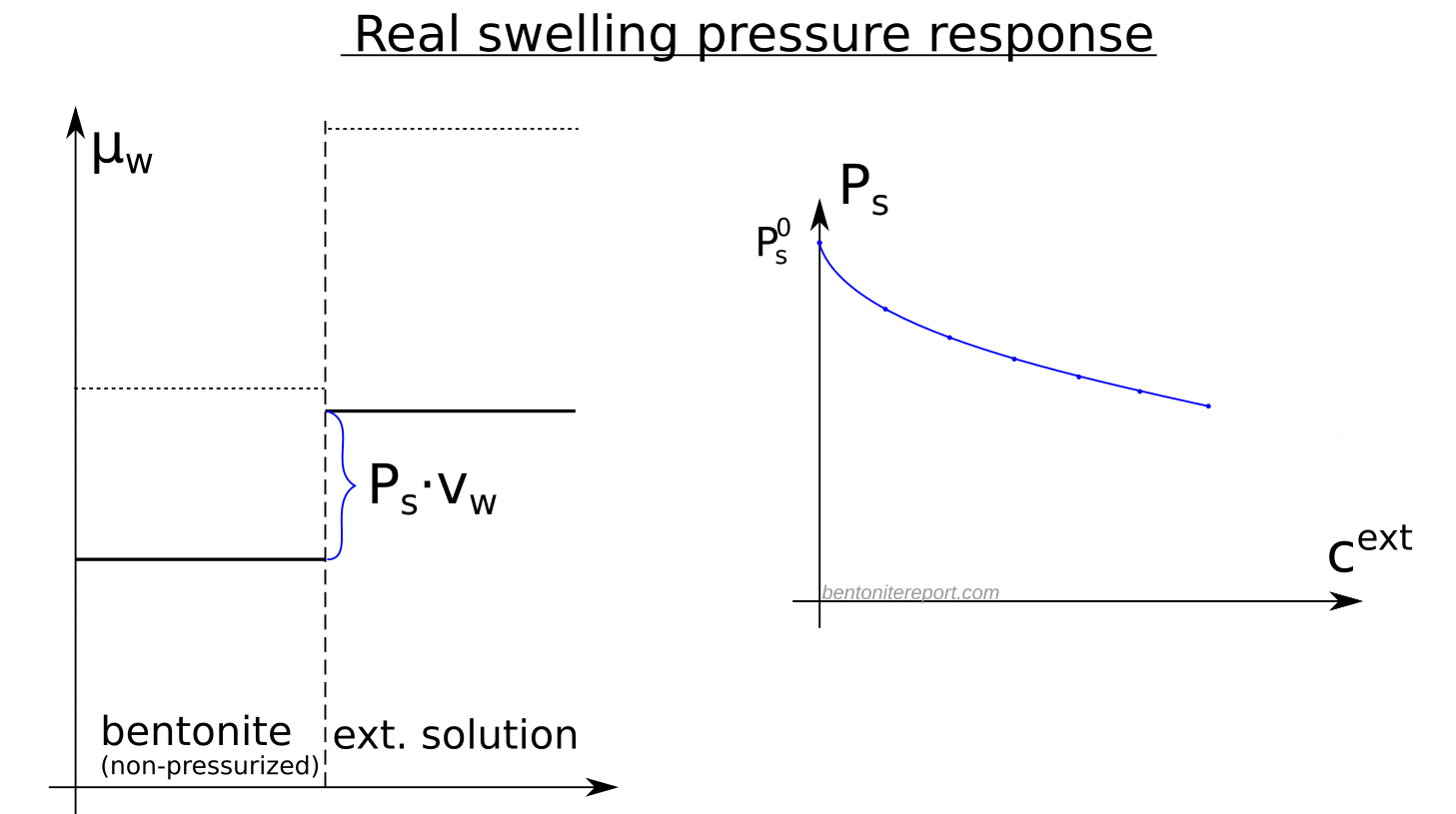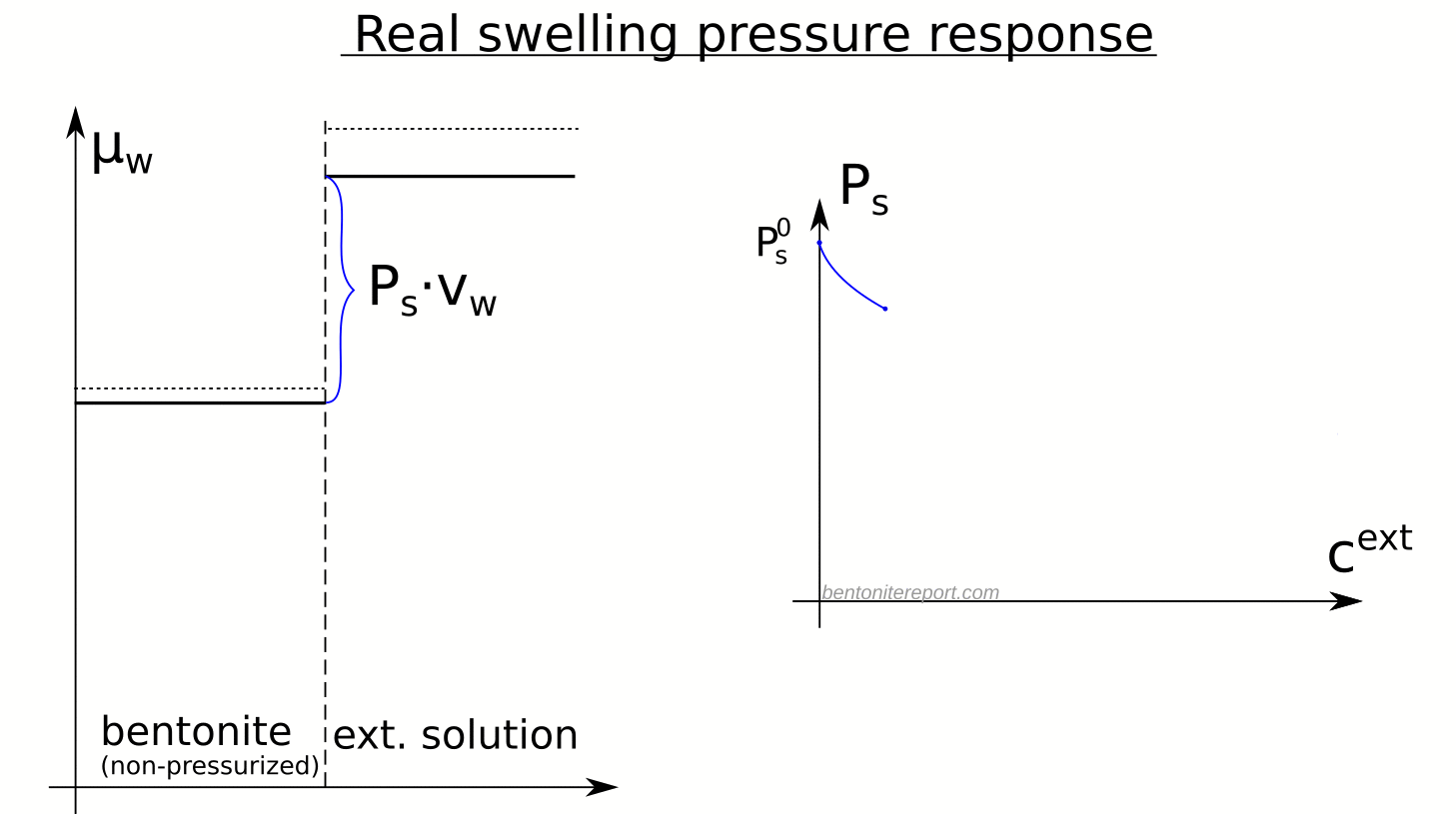
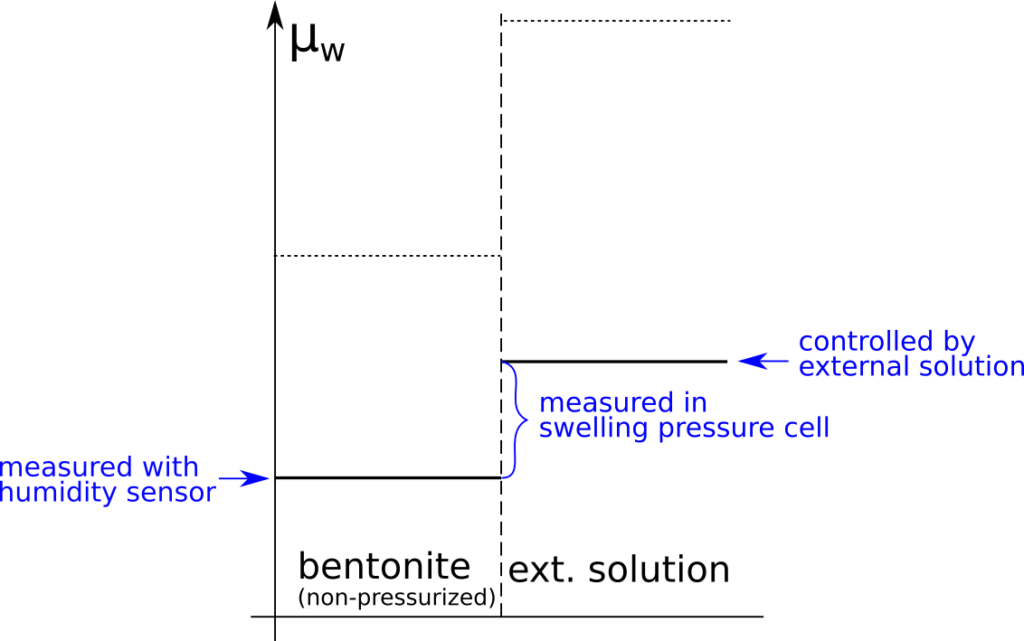
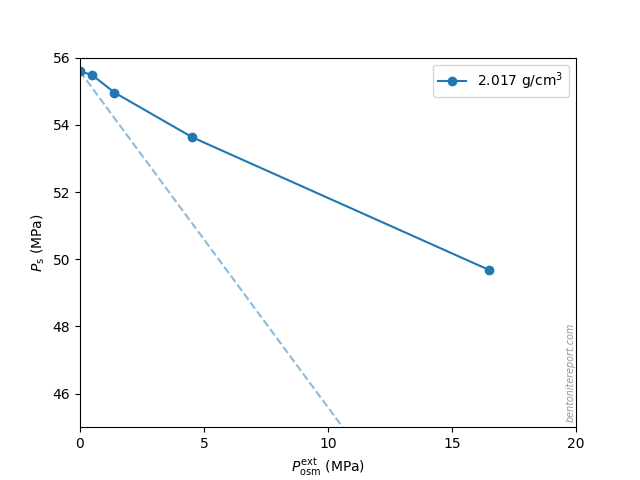
There are several “descriptions” of bentonite swelling. While a few of them actually denies any significant role played by the exchangeable cations, most of these descriptions treat the exchangeable ions as part of an osmotic system. I have earlier discussed how the terms “osmotic” or “osmosis” may cause some confusion in different contexts, and discussed the confusion surrounding the treatment of electrostatic forces.

In this blog post I discuss the description of bentonite swelling often adopted in the fields of soil mechanics and geotechnical engineering. In particular, we focus on the concept of suction, which is central in these research fields, while being basically absent in others.

As far as I understand, suction is just the water chemical potential “disguised” as a pressure variable; although I have trouble finding clear-cut definitions, it seems clear that suction is directly inherited from the “water potential” concept, which has been central in soil science for a long time. Applied to bentonite, the geotechnical description is thus not principally different from the osmotic approach that I have presented previously. But the way the suction concept is (and isn’t) applied may cause unnecessary confusion regarding the swelling mechanisms. I think a root for this confusion is that suction involves both osmotic and capillary mechanisms.

Matric suction (capillary suction)

Matric suction is typically associated with capillarity, a fundamental mechanism in many conventional soil materials under so-called unsaturated conditions. A conventional soil with a significant amount of small enough pores shows capillary condensation, i.e. it contains liquid water below the condensation point for ordinary bulk water. Naturally, the equilibrium vapor pressure increases with the amount of water in the soil, as the pores containing liquid water become larger. For conventional soils, it therefore makes sense to speak of the degree of saturation of a sample, and to relate saturation and equilibrium vapor pressure by means of a water retention curve. Underlying this picture is the notion that the solid parts constitute a “soil skeleton” (the matrix), and that the soil can be viewed as a vessel that can be more or less filled with water.

The pressure of the capillary water is lower than that of the surrounding air, and is related to the curvature of the interfaces between the two phases (menisci), as expressed by the Young-Laplace equation. For a spherically symmetric meniscus this equation reads

\begin{equation} \Delta p = p_w – p_a = \frac{2\sigma}{r} \tag{1} \end{equation}

where \(p_a\) and \(p_w\) denote the pressures of air and capillary water, respectively, \(\sigma\) is the surface tension, and \(r\) is the radius of curvature of the interface. The sign of \(r\) depends on whether the interface bulges inwards (“concave”, \(r<0\)) or outwards (“convex”, \(r>0\)). For capillary water, \(r\) is negative and \(\Delta p\) — which is also called the Laplace pressure — is a negative quantity.

As far as I understand, matric suction is simply defined as the negative Laplace pressure, i.e.

\begin{equation} s_m = p_a – p_w \tag{2} \end{equation}

With this definition, suction has a straightforward physical meaning as quantifying the difference in pressure of the two fluids occupying the pore space, and clearly relates to the everyday use of the word.

Suction — in this capillary sense — gives a simple principal explanation for (apparent) cohesion in e.g. unsaturated sand: individual grains are pushed together by the air-water pressure difference, as schematically illustrated here (the yellow stuff is supposed to be two grains of sand, and the blue stuff water)

Net force for two sand grains exposed to matric suction

It is reasonable to assume that the net force transmitted by the soil skeleton — usually quantified using the concept of effective stress — governs several mechanical properties of the soil sample, e.g. shear strength. The above description also makes it reasonable to assume that effective stress depends on suction.

Thus, in unsaturated conventional soil are quantities like degree of saturation, pore size distribution, (matric) suction, effective stress, and shear strength very much associated. Another way of saying this is that there is an optimal combination of water content and particle size distribution for constructing the perfect sand castle.

The chemical potential of the capillary water is related to matric suction. Choosing pure bulk water under pressure \(p_a\)¹ as reference, the chemical potential of the liquid phase in the soil is obtained by integrating the Gibbs-Duhem equation from \(p_a\) to \(p_w\)

\begin{equation} \mu = \mu_0 + \int_{p_a}^{p_w}v dP = \mu_0 + v\cdot \left(p_w – p_a \right) = \mu_0 -v\cdot s_m \tag{3} \end{equation}

where \(\mu_0\) is the reference chemical potential, \(v\) is the molar volume of water, and we have assumed incompressibility.

The above expression shows that matric suction in this case directly quantifies the (relative) water chemical potential. Note, however, that eq. 3 does not define matric suction; \(s_m\) is defined as a pressure difference between two phases (eq. 2), and happens to quantify the chemical potential under the present circumstances (pure capillary water).

A chemical potential can generally be expressed in terms of activity (\(a\))

\begin{equation} \mu = \mu_0 + RT \ln a \tag{4} \end{equation}

For our case, water activity is to a very good approximation equal to relative humidity, the ratio between the vapor pressures in the state under consideration and in the reference state, i.e. \(a = p_v/p_{v,0}\). Combining eqs. 3 and 4, we see that the vapor pressure in this case is related to matric suction as

\begin{equation} \frac{p_v}{p_{v,0}} = e^{-v\cdot s_m/RT} \end{equation}

Using the Young-Laplace equation (eq. 1) for \(s_m\) we can also write this as

\begin{equation} \frac{p_v}{p_{v,0}} = e^{\frac{2v\sigma}{RTr}} \end{equation}

This is the so-called Kelvin equation, which relates the equilibrium vapor pressure to the curvature of an air-pure water interface. Note that, since \(r<0\) for capillary water, the vapor pressure is lower than the corresponding bulk value (\(p_v < p_{v,0}\)).

Osmotic suction and total suction

So far, we have discussed suction in a capillary context, and related it to water chemical potential or vapor pressure. Now consider how the picture changes if the pores in our conventional soil contain saline water. Matric suction — i.e. the actual pressure difference between the pore solution and the surrounding air, sticking with eq. 2 as the definition — is in general different from the pure water case, because solutes influence surface tension. Also, water activity (vapor pressure) is different from the pure water case, but there is no longer a direct relation between water activity and matric suction, because water activity is independently altered by the presence of solutes.

The water chemical potential of a saline bulk solution (i.e. with no capillary effects), can be written in terms of the osmotic pressure, \(\pi(c)\)

\begin{equation} \mu(c) = \mu_0 – v\cdot\pi(c) \tag{5} \end{equation}

where we have assumed a salt concentration \(c\), and indicated that the osmotic pressure, and hence the chemical potential, depends on this concentration.

Although eq. 5 is of the same form as eq. 3, matric suction and osmotic pressure are very different quantities. The former is defined under circumstances where an actual pressure difference prevail between the air and water phases. In contrast, there is no pressure difference between the phases in a container containing both a solution and a gas phase. \(\pi(c)\) corresponds to the elevated pressure that must be applied for the solution to be in equilibrium with pure water kept at the reference pressure.

Despite the different natures of matric suction and osmotic pressure, the fields of geotechnical engineering and soil mechanics insist on also referring to \(\pi(c)\) as a suction variable: the osmotic suction. Similarly, total suction is defined as the sum of matric and osmotic suction

\begin{equation} \Psi = s_m + \pi(c) \end{equation}

These definitions seem to have no other purpose than to be able to write the water chemical potential generally as

\begin{equation} \mu = \mu_0 -v\cdot \Psi \tag{6} \end{equation}

Total suction is thus de facto defined simply as the (relative) value of the water chemical potential, expressed as a pressure (I think this is completely analogous to “total water potential” in soil science).

Eq. 6 shows that \(\Psi\) is directly related to water activity, or vapor pressure, and we can write

\begin{equation} \frac{p_v}{p_{v,0}} = e^{-v\cdot \Psi/RT} \tag{7} \end{equation}

This relation is quite often erroneously referred to as the Kelvin equation (or “Kelvin’s law”) in the bentonite literature. But note that the above equation just restates the definition of water activity, because \(v\cdot\Psi\) cannot be reduced to anything more concrete than the relative value of the water chemical potential. The Kelvin equation, on the other hand, expresses something more concrete: the equilibrium vapor pressure for a curved air-water interface. Some clay literature refer to the above relation as the “Psychrometric law”, but that name seems not established in other fields.²

A definition is motivated by its usefulness, and total change in water chemical potential is of course central when considering e.g. moisture movement in soil. My non-geotechnical brain, however, is not fond of extending the “suction” variable in the way outlined above. To start with, there is already a variable to use: the water chemical potential. Also, “total suction” no longer has the direct relation to the everyday use of the word suction: there is no “sucking” going on in a saline bulk solution,³ while in a capillary there is. Furthermore, with a saline pore solution there is no direct relation between (total) suction and e.g. effective stress or shear strength.

Although both matric suction and osmotic pressure under certain circumstances can be measured in a direct way, it seems that (total) suction usually is quantified by measuring/controlling the vapor pressure with which the soil sample is in equilibrium. Actually, one of the more comprehensive definitions of various “suctions” that I have been able to find — in Fredlund et al. (2012) — speaks only of various vapor pressures (although based on the capillary and osmotic concepts):⁴

Matric or capillary component of free energy: Matric suction is the equivalent suction derived from the measurement of the partial pressure of the water vapor in equilibrium with the soil-water relative to the partial pressure of the water vapor in equilibrium with a solution identical in composition with the soil-water.

Osmotic (or solute) component of free energy: Osmotic suction is the equivalent suction derived from the measurement of the partial pressure of the water vapor in equilibrium with a solution identical in composition with the soil-water relative to the partial pressure of water vapor in equilibrium with free pure water.

Total suction or free energy of soil-water: Total suction is the equivalent suction derived from the measurement of the partial pressure of the water vapor in equilibrium with the soil-water relative to the partial pressure of water vapor in equilibrium with free pure water.

It seems that such operational definitions of suction has made the term synonymous with “vapor pressure depression” in large parts of the bentonite scientific literature.

Suction in bentonite

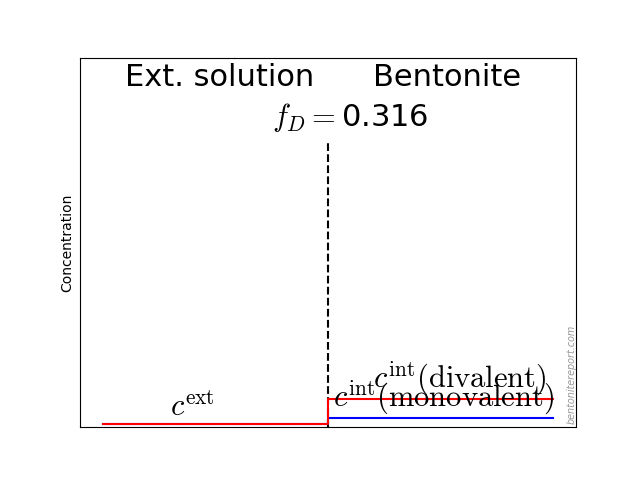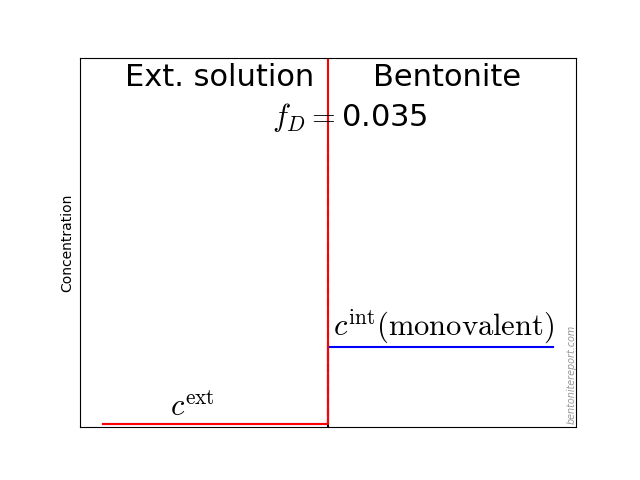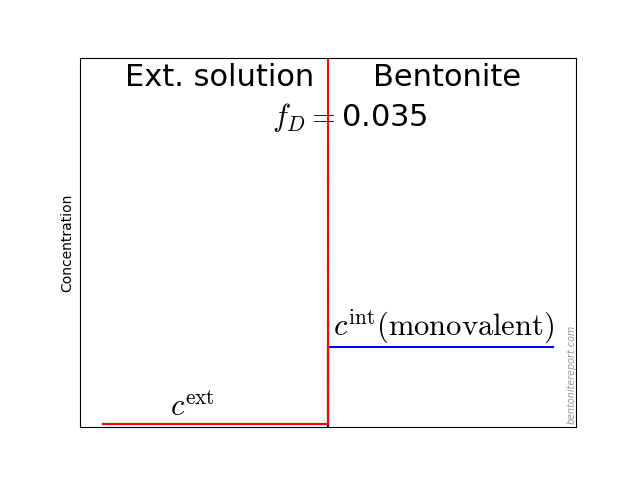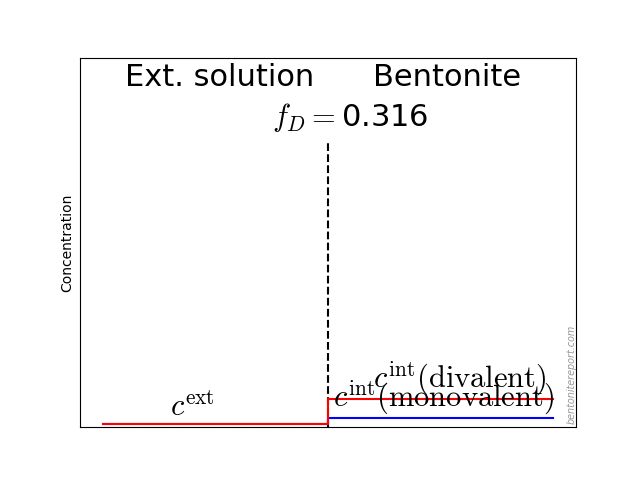
In the above discussion we had mainly a conventional soil in mind. When applying the suction concepts to bentonite,⁵ I think there are a few additional pitfalls/sources for confusion. Firstly, note that the definitions discussed previously involve “a solution identical in composition with the soil-water”. But soil-water that contains appreciable amounts of exchangeable ions — as is the case for bentonite — cannot be realized as an external solution.

It seems that this “complication” is treated by assuming that an external solution in equilibrium with a bentonite sample is the soil-water (this is analogous to how many geochemists use the term “porewater” in bentonite contexts). Not surprisingly, this treatment has bizarre consequences. The conclusion for e.g. a salt free bentonite sample — which is in equilibrium with pure water — is that it lacks osmotic suction, and that its lowered vapor pressure (when isolated and unloaded) is completely due to matric suction! I think this is such an odd outcome that it is worth repeating: A system dominated by interlayer pores, containing dissolved cations at very high concentrations, is described as lacking osmotic pressure! It is not uncommon to find descriptions like this one (from Lang et al. (2019))

The total suction of unsaturated soils consists of matric and osmotic suctions (Yong and Warkentin, 1975; Fredlund et al., 2012; Lu and Likos, 2004). In clays, the matric suction is due to surface tension, adsorptive forces and osmotic forces (i.e. the diffuse double layer forces), whereas the osmotic suction is due to the presence of dissolved solutes in the pore water.

We apparently live in a world where “matric suction” consists of “osmotic forces”, while the same “osmotic forces” do not contribute to “osmotic suction”. Except when the clay contains excess ions, in which case we have an arbitrary combination of the two “suctions” (note also that “osmotic suction” and “osmotic swelling” are two quite different things).

Although the above consequence is odd, it is still only a matter of definition: accepting that “matric suction” involves osmotic forces (which I don’t recommend), the description may still be adequate in principle; after all, “total suction” quantifies the reduction of the water chemical potential.

But the focus on “matric suction” also reveals a conceptual view of bentonite structure that I find problematic: it suggests a first order approximation of bentonite as a conventional soil, i.e. as an assemblage of solid grains separated from an aqueous phase (and a gas phase). This “matric” view is fully in line with the idea of “free water” in bentonite, and it is quite clear that this is a prevailing view in the geotechnical, as well as in the geochemical, literature. For instance, with the formulation “the presence of dissolved solutes in the pore water” in the above quotation, the “pore water” the authors have in mind is a charge neutral bulk water solution.

With the “matric” conceptual view, the degree of saturation becomes a central variable in much soil mechanical analyses of bentonite. When dealing with actual unsaturated bentonite samples, I guess this makes sense, but once a sample is saturated this variable has lost much of its meaning.⁶ Consider e.g. the different expected behaviors if drying e.g. a water saturated metal filter or a saturated bentonite sample.

The different nature of drying a metal filter compared with drying a saturated bentonite sample

The equilibrium vapor pressure of both these systems is lower than the corresponding pure bulk water value. For the metal filter, the lowered water activity is of course due to capillarity, i.e. there is an actual pressure reduction in the water phase (matric suction!). When lowering the external vapor pressure below the equilibrium point (i.e. drying), capillary water migrates out of the filter, while the metal structure itself remains intact. In this case, as the system remains defined in a reasonable way, it is motivated to speak of the saturation state of the filter.

For a drying bentonite sample, the behavior is not as well defined, and depends on how the drying is performed and on initial water content. For a quasi-static process, where the external vapor pressure is lowered in small steps at an arbitrary slow rate, it should be clear that the entire sample will respond simply by shrinking. In this case it does not make much sense to speak of the sample as still being saturated, nor to speak of it as having become unsaturated.

For a more “violent” drying process, e.g. placing the bentonite sample in an oven at 105 °C , it is also clear that — rather than resulting in a neatly shrunken, dense piece of clay — the sample now will suffer from macroscopic cracks and other deformations. Neither in this case does it make much sense to try to define the degree of saturation, in relation to the sample initially put in the oven.

Note also that if we, instead of drying, increase the external vapor pressure from the initial equilibrium value, the metal filter will not respond much at all, while the bentonite sample immediately will begin to swell.

I hope that this example has made it clear, not only that the degree of saturation is in general ill-defined for bentonite, but also that a bentonite sample behaves more as an aqueous solution rather than as a conventional soil: if we alter external vapor pressure, an aqueous solution responds by either “swelling” (taking up water) or “shrinking” (giving off water). A main aspect of this conceptual view of bentonite — which we may call the “osmotic” view — is that water does not form a separate phase⁷. This was pointed out e.g. by Bolt and Miller (1958) (referring to this type of system as an “ideal clay-water system”)

In contrast to the familiar case described is the ideal clay-water system in which the particles are not in direct contact but are separated by layers of water. Removal of water from such a system does not introduce a third phase but merely causes the particles to move closer to one another with the pores remaining water saturated.

From these considerations it follows that a generally consistent treatment is to relate bentonite water activity to water content, rather than to degree of saturation.

Another consequence of adopting a “matric” view of bentonite (i.e. to include osmotic forces in “matric suction”) is that “matric suction” loses its direct connection with effective stress. This can be illustrated by taking the “osmotic” view: just as the mechanical properties of an aqueous solution (e.g. viscosity) do not depend critically on whether or not it is under (osmotic) pressure, we should not expect e.g. bentonite shear strength to be directly related to swelling pressure.⁸

Footnotes

[1] Often, the air is at atmospheric pressure, in which case the reference is the ordinary standard state.

[2] The relatively common misspelling “Psychometric law” is kind of funny.

[3] The cautious reader may remark that saline solutions do “suck”, in terms of osmosis. But note the following: 1) Osmosis requires a semi-permeable membrane, separating the solution from an external water source. We have said nothing about the presence of such a component in the present discussion. The way osmotic suction sometimes is described in the literature makes me suspect that some authors are under the impression that the mere presence of a solute causes a pressure reduction in the liquid. 2) In the presence of a semi-permeable membrane, osmosis has no problem occurring without a pressure difference between between the two compartments. 3) For cases when the solution is acted on by an increased hydrostatic pressure, water is transported from lower to higher pressure. It is difficult to say that there is any “sucking” in such a process (I would argue that the establishment of a pressure difference is an effect, rather than a cause, in the case of osmosis) 4) The idea that a solution has a well-defined partial water pressure is wrong.

[4] I’m still not fully satisfied with this definition: It may be noted that the definitions are somewhat circular (“matric suction is the equivalent suction…”), so they still require that we have in mind that “suction” also is defined in terms of a certain vapor pressure ratio (e.g. eq. 7). Note also that the headings speak of “free energy”. Perhaps I am nitpicking, but (free) energy is an extensive quantity, while suction (pressure) is intensive. Thus, “free energy” here really mean “specific free energy” (or “partial free energy”, i.e. chemical potential). I think the soil science literature in general is quite sloppy with making this distinction.

[5] “Bentonite” is used in the following as an abbreviation for bentonite and claystone, or any clay system with significant cation exchange capacity.

[6] If you press bentonite granules to form a cohesive sample you certainly end up with a system having both water filled interlayer pores and air-filled macropores (or perhaps an even more complex pore structure). This blog post mainly concerns saturated bentonite, by which I mean bentonite material which does not contain any gas phase. We can thus speak of saturated bentonite, although a degree of saturation variable is not well defined.

[7] Rather, montmorillonite and water form a homogeneous mixture.

[8] However, bentonite strength relates indirectly to swelling pressure (under specific conditions) because both quantities depends on a third: density.

Donnan equilibrium and the homogeneous mixture model

Leave a reply

We can directly apply the homogeneous mixture model for bentonite to isolated systems — e.g. closed-cell diffusion tests — as discussed previously. For systems involving external solutions we must also handle the chemical equilibrium at solution/bentonite interfaces.

I have presented a framework for calculating the chemical equilibrium between an external solution and a bentonite component in the homogeneous mixture model here. In this post I will discuss and illustrate some aspects of that work.

Overview

We assume a homogeneous bentonite domain in contact with an external solution, with the clay particles prevented from crossing the domain interface. For real systems, this corresponds to the frequently encountered set-up with bentonite confined in a sample holder by means of e.g. a metal filter. From the assumptions of the homogeneous model — that all ions are mobile and allowed to cross the domain interface — it follows that the type of equilibrium to consider is the famous Donnan equilibrium. I have discussed the Donnan effect and its relevance for bentonite quite extensively here.

Since the adopted model assumes a homogeneous bentonite domain, the only region where Donnan equilibrium comes into play is at the interface between the bentonite and the external solution. This is quite different from how Donnan equilibrium calculations are implemented in many multi-porous models, where the equilibrium is internal to the clay — between assumed “macro” and “micro” compartments of the pore structure. The need for performing Donnan equilibrium calculations is thus minimized in the homogeneous mixture model (as mentioned, isolated systems require no such calculations). Note also that the semi-permeable mechanism in multi-porous models is required to act on the pore-scale. I have never seen any description or explanation how such a mechanism is supposed to work.¹ In the homogeneous mixture model, on the other hand, the semi-permeable interface corresponds directly to a macroscopic and experimentally well-defined component: the confining filter.

The problem to be solved can be illustrated like this

Schematic illustration of an external solution in contact with a homogeneous bentonite domain

The aim is to relate the set of species concentrations in the external solution (\(\{c_i^\mathrm{ext}\}\)) to those in the clay domain (\(\{c_i^\mathrm{int}\}\)) when the system is in equilibrium. This is done by applying the standard approach to Donnan equilibrium, as found in textbooks on the subject. If there is anything “radical” about this framework, it is thus not in the way Donnan equilibrium is implemented, but rather in treating bentonite as a single phase: this approach is formally equivalent to assuming the bentonite to be an aqueous solution.

Chemical equilibrium

I prefer to formulate the Donnan equilibrium framework in a way that separates effects due to difference in the local chemical environment from effects due to differences in electrostatic potential between the two compartments. An important reason for focusing on this separation is that the local environment affects the chemistry under all circumstances, while the (relative) value of the electrostatic potential only is relevant when bentonite is contacted with an external solution. We therefore express the chemical equilibrium as

\begin{equation} \frac{c_i^\mathrm{int}}{c_i^\mathrm{ext}} = \frac{\gamma_i^\mathrm{ext}}{\gamma_i^\mathrm{int}}\cdot e^{-\frac{z_iF\psi^\star}{RT}} \tag{1} \end{equation}

This formula is achieved by setting the electro-chemical potential equal for each species in the two compartments. Here \(\gamma_i\) denotes the activity coefficient for species \(i\), and \(\psi^*\) is the electrostatic potential difference between the compartments, which we refer to as the Donnan potential.

I find it convenient to rewrite this expression using some fancy Greek letters

\begin{equation} \label{eq:chem_eq2} \Xi_i = \Gamma_i \cdot f_D^{-z_i} \tag{2} \end{equation}

Here I call \(\Xi_i = c_i^\mathrm{int}/c_i^\mathrm{ext}\) the ion equilibrium coefficient for species \(i\). This quantity expresses the essence of ion equilibrium in the homogeneous mixture model, and will appear in many places in the analysis. \(\Xi_i\) has two factors:

\(\Gamma_i = \gamma_i^\mathrm{ext}/\gamma_i^\mathrm{int}\) expresses the chemical aspect of the equilibrium: when \(\Gamma_i\) is large (\(>1\)), the species has a chemical preference for residing in the interlayer pores, and when \(\Gamma_i\) is small (\(<1\)), the species has a preference for the external solution. In general, \(\Gamma_i\) for any specific species \(i\) is a function of all species concentrations in the system.
\(f_D^{-z_i}\), where \(f_D = e^{\frac{F\psi^\star}{RT}}\) is a dimensionless transformation of the Donnan potential (this is basically the Nernst equation), which we here call the Donnan factor. \(f_D\) expresses the electrostatic aspect of the equilibrium, and is the same for all species. The effect on \(\Xi_i\), however, is different for species of different charge number, because of the exponent \(-z_i\) in the full expression.

I want to emphasize that eqs. 1 and 2 express the exact same thing: chemical equilibrium between the two compartments.

Illustrations

To get a feel for the quantity \(\Xi\), here is a hopefully useful animation

Relation beteween internal and external concentration for varying Xi

It may also be helpful to see the influence of \(f_D\) on the equilibrium. Since the Donnan potential is negative, \(f_D\) is less than unity and typical values in relevant bentonite systems is \(f_D \sim\) 0.01 — 0.4. Due to the exponent \(-z_i\) in eq. 2, this influence on the equilibrium looks quite different for species with different valency. For mono- and di-valent cations, the behavior looks like this (here is put \(\Gamma = 1\) for both species)

Variation of internal cation concentrations with varying Donnan factor

The typical behavior for cations is that the internal concentration is much larger than the corresponding external concentration (at \(f_D = 0.01\) in the above animation, the internal concentration for the di-valent cation is enhanced by a factor \(\Xi = 10 000\)!). For anions, the internal concentration is instead lower than the external concentration,² as shown here (\(\Gamma = 1\) for both species)

Variation of internal anion concentration with the Donnan factor

Equation for \(f_D\)

For a complete description, we need an equation for calculating \(f_D\). This is derived by requiring charge neutrality in the two compartments and look like

\begin{equation*} \sum_i z_i\cdot\Gamma_i \cdot c_i^\mathrm{ext} \cdot f_D^{-z_i} – c_{IL} = 0 \tag{3} \end{equation*}

where

\begin{equation*} c_{IL} = \frac{CEC}{F \cdot w} \end{equation*}

is the structural charge present in the clay (i.e. negative montmorillonite layer charge) expressed as a monovalent interlayer concentration. Here \(CEC\) is the cation exchange capacity of the clay component, \(w\) the water-to-solid mass ratio,³ and \(F\) is the Faraday constant.

The way eq. 3 is formulated implies that the external concentrations should be used as input to the calculation. This is typically the case as the external concentrations are under experimental control.

In typical geochemical systems it is required to account for aqueous species with valency at least in the range -2 — +2 (e.g. \(\mathrm{Ca}^{2+}\), \(\mathrm{Na}^{+}\), \(\mathrm{Cl}^{-}\), \(\mathrm{SO_4}^{2-}\)), which implies that the equation for calculating \(f_D\) is generally a polynomial equation of degree four or higher.

An important special case is the 1:1 system — e.g. pure Na-montmorillonite contacted with a NaCl solution — which has an equation for \(f_D\) of only degree two, and thus have a relatively simple analytical solution

\begin{equation*} f_D = \frac{c_{IL}}{2c^\mathrm{ext} \Gamma_\mathrm{Cl}} \left ( \sqrt{1+ \frac{4(c^\mathrm{ext})^2 \Gamma_\mathrm{Na}\Gamma_\mathrm{Cl}} {c_{IL}^2}} – 1 \right ) \end{equation*}

With the machinery in place for calculating the Donnan potential, here is an animation demonstrating the response in internal sodium and chloride concentrations as the external NaCl concentration is varied. In this calculation \(c_{IL} = 2\) M, and \(\Gamma_\mathrm{Na} = \Gamma_\mathrm{Cl} = 1\)

Relation between internal and external Na and Cl concentrations

Comment on through-diffusion

To me, the last illustration makes it absolutely clear that Donnan equilibrium and the homogeneous mixture model provide the correct principal explanation for e.g. the behavior of tracer ions in through-diffusion tests. If you choose to relate the flux in through-diffusion tests to the external concentration difference — which is basically done in all published studies, via the parameter \(D_e\) — you will evaluate large “diffusivities” for cations and small “diffusivities” for anions. These “diffusivities” will, moreover, have the opposite dependence on background concentration: the cation flux diverges in the low background concentration limit,⁴ while the anion flux approaches zero.

But this behavior is seen to be caused by differently induced internal concentration gradients. If fluxes are related to these gradients — which they of course should, if you strive for an actual Fickian description — you find that the diffusivities are no different from what is evaluated in closed-cell tests. Relating the steady-state flux to the external concentration difference in the homogeneous mixture model gives (assuming zero tracer concentration on the outflow side)

\begin{equation*} j_\mathrm{ss} = -\phi\cdot D_c \cdot \nabla c^\mathrm{int} = \phi\cdot D_c \cdot\Xi\cdot \frac{c^\mathrm{source}}{L} \end{equation*}

where \(c^\mathrm{source}\) denotes the tracer concentration in the external solution on the inflow side, \(\phi\) is the porosity, \(D_c\) is the pore diffusivity in the interlayer domain, and \(L\) is the length of the bentonite sample. From the above equation can directly be identified

\begin{equation} D_e = \phi\cdot\Xi\cdot D_c \end{equation}

\(D_e\) is thus not a diffusion coefficient, but basically a measure of \(\Xi\).

Note that this explanation for the behavior of \(D_e\) does not invoke any notion of an anion accessible volume, nor any “sorption” concept for cations.⁵

Additional comments

When I first published on Donnan equilibrium in bentonite, I was a bit confused and singled out the term “Donnan equilibrium” to refer to anions only, while calling the corresponding cation equilibrium “ion-exchange equilibrium”. To refer to “both” types of equilibrium we used the term “ion equilibrium”.⁶ Of course, Donnan equilibrium applies to ions of any charge and, being better informed, I should have used a more stringent terminology. In later publications I have tried to make amends by pointing out that the process of cation exchange is part of the establishment of Donnan equilibrium.

Being new to the Donnan equilibrium world, I also invented some of my own nomenclature and symbols: e.g. I named the ratio between internal and external concentration the ion equilibrium coefficient (\(\Xi\)). Conventionally, if I now have understood correctly, this concentration ratio is referred to as the “Donnan ratio”, and is usually labeled \(r\) (although I’ve also seen \(K\)).

But the term “Donnan ratio” seems to be used slightly differently in different contexts, e.g. defined either as \(c^\mathrm{int}/c^\mathrm{ext}\) or as \(c^\mathrm{ext}/c^\mathrm{int}\), and is sometimes related more directly to the Donnan potential (if no distinction is made between activities and concentrations, we can write \(f_D^{-z_i} = c_i^\mathrm{int}/c_i^\mathrm{ext}\)). I therefore will continue to use the term “ion equilibrium coefficient” — with label \(\Xi\) — in the context of bentonite systems. This usage has also been picked up in some other clay publications. The ion equilibrium coefficient should be understood as strictly defined as \(\Xi = c^\mathrm{int}/c^\mathrm{ext}\) for any species, and never to define, or being defined by, the Donnan potential.

To emphasize the difference between effects due to the presence of a Donnan potential and effects due to different local chemical environments, I will refer to \(f_D\) as the Donnan factor. (This term does not seem to be used conventionally for any other quantity, although there are examples where it is used as a synonym for Donnan ratio.)

Finally, as in any other approach, the current framework requires a description for the activity coefficients. For activity coefficients in the external solution, there are quite a number of models already available. For the interlayer, modeling — and measuring! — activities is an open research area (at least I hope that this research area is open).

Footnotes

[1] This is just one of several major “loose ends” in most multi-porous models. I have earlier discussed the lack of treatment of swelling, and the incorrect treatment of fluxes in different domains. Update (220622): The lack of a semi-permeable component in multi-porosity models is further discussed here.

[2] This does not have to be the case in principle, if \(\Gamma\) for the anion is large, at the same time as the external concentration is not too low.

[3] Hence, it is implied that we use concentration units based on water mass (molality).

[4] What actually happens is that the transport resistance in the filters begins to dominate.

[5] Speaking of “sorption”, we have noted before that this term nowadays is used to mean any type of uptake between bulk water and some other domain (where the species may or may not be immobile). In this sense, there is “sorption” in the homogeneous mixture model (for both cations and anions), but only at interfaces to external solutions. It thus translates to a boundary condition, rather than being part of the transport dynamics within the clay (which makes life much simpler from a numeric perspective). Update (220622): The homogeneous mixture model is extended to deal with ions that truly sorbs here.

[6] It turns out Donnan himself actually used this terminology (“ionic equilibria”)

Sorption part III: Donnan equilibrium in compacted bentonite

Leave a reply

Consider this basic experiment: contact a water saturated sample of compacted pure Na-montmorillonite, with dry mass 10 g and cation exchange capacity 1 meq/g, with an external solution of 100 ml 0.1 M KCl. Although such an experiment has never been reported¹, I’m convinced that all agree that the outcome would be similar to what is illustrated in this animation.

Potassium diffuses in, and sodium diffuses out of the sample until equilibrium is established. At equilibrium also a minor amount of chloride is found in the sample. The indicated concentration levels are chosen to correspond roughly to results from from similar type of experiments.²

Although results like these are quite unambiguous, the way they are described and modeled in the bentonite³ literature is, in my opinion, quite a mess. You may find one or several of the following terms used to describe the processes

Cation exchange
Sorption/Desorptioṇ
Anion exclusion
Accessible porosity
Surface complexation
Donnan equilibrium
Donnan exclusion
Donnan porosity/volume
Stern layer
Electric double layer
Diffuse double layer
Triple layer
Poisson-Boltzmann
Gouy-Chapman
Ion equilibrium
…

In this blog post I argue for that the primary mechanism at play is Donnan equilibrium, and that most of the above terms can be interpreted in terms of this type of equilibrium, while some of the others do not apply.

Donnan equilibrium: effect vs. model

In the bentonite literature, the term “Donnan” is quite heavily associated with the modeling of anion equilibrium; e.g. the term “Donnan exclusion” is quite common , and you may find statements that researchers use “Donnan porespace models” as models for “anion exclusion”, or a “Donnan approach” to model “anion porosity”.⁴ Sometimes the term “Donnan effect” is used synonymously with “Salt exclusion”. Also when authors acknowledge cations as being part of “Donnan” equilibrium, the term is still used mainly to label a model or an “approach”.

But I would like to push for that “Donnan equilibrium” primarily should be the name of an observable effect, and that it applies equally to both anions and cations. This effect — which was hypothesized by Gibbs already in the 1870s — relies basically only on two things:

An electrolytic system, i.e. the presence of charged aqueous species (ions).
The presence of a semi-permeable component that is permeable to some of the charges, but does not allow for the passage of at least one type of charge.

In equilibrated systems fulfilling these requirements it is — to use Donnan’s own words — “thermodynamically necessary” that the permeant ions distribute unequally across the semi-permeable component. This phenomenon — unequal ion distributions on the different sides of the semi-permeable component — should, in my opinion, be the central meaning of the term “Donnan equilibrium”.

The first publication of Donnan on the effect actually concerned osmotic pressure response, in systems of Congo Red separated from solutions of sodium chloride and sodium hydroxide. The same year (1911) he also published the ionic equilibrium equations for some specific systems.⁵ In particular he considered the equilibrium of NaCl initially separated from NaR, where R is an impermeant anion (e.g. that of Congo Red), leading to the famous relation (“int” denotes the solution containing R)

\begin{equation} c_\mathrm{Na^+}^\mathrm{ext}\cdot c_\mathrm{Cl^-}^\mathrm{ext} = c_\mathrm{Na^+}^\mathrm{int}\cdot c_\mathrm{Cl^-}^\mathrm{int} \tag{1} \end{equation}

Unfortunately, this relation alone (or relations derived from it) is often what the term “Donnan” is associated with in today’s clay research literature, with the implication that systems not obeying it are not Donnan systems. But the above relation assumes ideal conditions and complete ionization of the salts — issues Donnan persistently seems to have grappled with. In a review on the effect he writes

The exact equations can, however, be stated only in terms of the chemical potentials of Willard Gibbs, or of the ion activities or ionic activity-coefficients of G. N. Lewis. Indeed an accurate experimental study of the equilibria produced by ionically semi-permeable membranes may prove to be of value in the investigation of ionic activity coefficients.

It must therefore be understood that, if in the following pages ionic concentrations and not ionic activities are used, this is done in order to present a simple, though only approximate, statement of the fundamental relationships.

The issue of (the degree of) ionization was explicitly addressed in publications following the 1911 article; Donnan & Allmand (1914) motivated their investigations of the \(\mathrm{KCl/K_4Fe(CN)_6}\) system by that “it was deemed advisable to test the relation when using a better defined, non-dialysable anion than that of Congo-red”, and the study of the Na/K equilibrium in Donnan & Garner (1919) used ferrocyanide solutions on both sides of the membrane in an attempt to overcome the difficulty of the “uncertainty as to the manner of ionisation of potassium ferrocyanide” (and thus for the simplified equations to apply).

I mean that since non-ideality and ion association are general issues when treating salt solutions, it does not make much sense to use the term “Donnan equilibrium” only when some particular equation applies; as long as the mechanism for the observed behavior is that some charges diffuse through a semi-permeable component, while some others don’t, the effect should be termed Donnan equilibrium.

Donnan equilibrium in gels, soils and clays

After Donnan’s original publications in 1911, the effect was soon recognized in colloidal systems. Procter & Wilson (1916) used Donnan’s equations to analyze the swelling of gelatin jelly immersed in hydrochloric acid. In this case chloride is the charge compensating ion, allowed to move between the phases, while the immobile charge is positive charges on the gelatin network. Thus, no semi-permeable membrane is necessary for the effect; alternatively one could say that the gel constitutes its own semi-permeable component. The Donnan equilibrium in protein solutions was further and extensively investigated by Loeb.

As far as I am aware, Mattson was first to identify the Donnan effect in “soil” suspensions,⁶ attributing e.g. “negative adsorption” of chloride as a consequence of Donnan equilibrium, and explicitly referencing the works of Procter and Loeb. Mattson describes the suspension in terms of electric double layers with a diffuse “atmosphere of cations” surrounding the “micelle” (the soil particle), and refers to Donnan equilibrium as the distribution of an electrolyte between the “micellar” and the “inter-micellar” solutions. Oddly,⁷ he uses Donnan’s original framework (e.g. eq. 1) to quantify the equilibrium, although the electrostatic potential and the ion concentrations varies significantly in the investigated systems. A more appropriate treatment would thus be to use e.g. the Gouy-Chapman description for the ion distribution near a charged plane surface (which he refers to!).

Instead, Schofield (1947) analyzed Mattson’s data using this approach. He also comments on its (the Gouy-Chapman model) range of validity

… [T]he equation is applicable to cases in which the distance between opposing surfaces considerably exceeds the distance between neighboring point charges on the surfaces; for there will then be a range of electrolyte concentrations over which the radius of the ionic atmosphere is less than the former and greater than the latter. In Mattson’s measurements on bentonite suspension, these distances are roughly 500 A. and 10 A. respectively, so there is an ample margin.

He continues to comment on the validity of Donnan’s original equations

When the distance ratio has narrowed to unity, it is to be expected that the system will conform to the equation of the Donnan membrane equilibrium. This equation fits closely the measurements of Procter on gelatine swollen in dilute hydrochloric acid. […] In a bentonite suspension the charges are so far from being evenly distributed that the Donnan equation is not even approximately obeyed.

From these statements it should be clear that the general behavior (cation exchange, salt exclusion) of ions in bentonite equilibrated with an external solution is due to the Donnan effect.⁸ The appropriate theoretical treatment of this effect differs, however, depending on details of the investigated system. To argue whether or not e.g. the Gouy-Chapman description should be classified as a “Donnan” approach is purely semantic.

It is also clear that in the case of compacted bentonite the distance ratio is narrowed to unity — the typical interlayer distance is 1 nm, which also is the typical distance between structural charges in the montmorillonite particles. It is thus expected that Donnan’s original treatment may work for such systems (adjusted for non-ideality), while the Gouy-Chapman description is not valid.⁹

The message I am trying to convey is neatly presented in Overbeek (1956) — a text I highly recommend for further information. Overbeek distinguishes between “classical” (Donnan’s original) and “new” (accounting for variations in potential etc.) treatments of Donnan equilibrium, and says the following about dense systems

If the particles come very close together the potential drop between [surface and interlayer midpoint] becomes smaller and smaller as illustrated in Fig. 4. This means that the local concentrations of ions are not very variable and that we are again back at the classical Donnan situation, where distribution of ions, osmotic pressure and Donnan potential are simply given by the elementary equations as treated in section 2. It is remarkable that the new treatment of the Donnan effects may deviate strongly from the classical treatment when the colloid concentration is low, but not when it is high.

It thus seems plausible that Donnan equilibrium in compacted bentonite can be treated using Donnan’s original equations. But — as interlayer pores is a quite extreme chemical environment — substantial non-ideal behavior may be expected. Treating such behavior is a large challenge for chemical modeling of compacted bentonite, but can not be avoided, since interlayers dominate the pore structure.

Cation exchange is Donnan equilibration

The term “Donnan” in modern bentonite literature is, as mentioned, quite heavily associated with the fate of anions interacting with bentonite. In contrast, cations are often described as being “sorbed” onto the “solids”. This sorption is usually separated into two categories: cation exchange and surface complexation.

Surface complexation reactions are typically described using “surface sites”, and are usually written something like this (exemplified with sodium sorption)

\begin{equation} \equiv \mathrm{S^-} + \mathrm{Na^{+}(aq)} \leftrightarrow \equiv \mathrm{SNa} \end{equation}

where the “surface site” is labeled \(\equiv \mathrm{S}^-\)

Cation exchange is also typically written in terms of “sites”, but requires the exchange of ions (duh!), like this (here exemplified for calcium/sodium exchange)

\begin{equation} \mathrm{2XNa} + \mathrm{Ca^{2+}(aq)} \leftrightarrow \mathrm{X_2Ca} + 2\mathrm{Na^+(aq)} \tag{2} \end{equation}

where X represents an “exchange site” in the solid phase.

In the clay literature the distinction between “surface complexation” and “ion exchange” reactions is rather blurred. You can e.g. find statements that “the ion exchange model can be seen as a limiting case of the surface complex model…”, and it is not uncommon that ion exchange is modeled by means of a surface complexation model. It also seems rather common that ion exchange is understood to involve surface complexation.

Underlying these modeling approaches and descriptions is the (sometimes implicit) idea that exchanged ions are immobile, which clearly has motivated e.g. the traditional diffusion-sorption model for bentonite and claystone. This model assumes that ion exchange binds cations to the solid, making them immobile, while diffusion occurs solely in a bulk water phase (which, incredibly, is assumed to fill the entire pore volume).

However, the idea that the exchanged ion is immobile does not agree with descriptions in the more general ion exchange literature, which instead acknowledge the process as an aspect of the Donnan effect.

Indeed, already in 1919, Donnan & Garner reported Na/K exchange equilibrium in a system consisting of two ferrocyanide solutions separated by a membrane impermeable to ferrocyanide, and it is fully clear that the particular distribution of cations in such systems is just as “thermodynamically necessary” as the distribution of chloride in the initial work on Congo Red and ferrocyanide.

Applied to clays, it is clear that cation exchange occurs even without postulating specific “sorption sites” or immobilization. On the contrary, ion exchange occurs in Donnan systems precisely because the ions are mobile.

In his book “Ion exchange”,¹⁰ Freidrich Helfferich describes ion exchange as diffusion, and distinguishes it from “chemical” processes

Occasionally, ion exchange has been referred to as a “chemical” process, in contrast to adsorption as a “physical” process. This distinction, though plausible at first glance, is misleading. Usually, in ion exchange as a redistribution of ions by diffusion, chemical factors are less significant than in adsorption where the solute is held by the sorbent by forces which may not be purely electrostatic.

Furthermore, in describing a general ion exchange system, he states the exact characteristics of a Donnan system, with the crucial point that the exchangeable ion is “free”, albeit subject to the constraint of electroneutrality

Ion exchangers owe their characteristic properties to a peculiar feature of their structure. They consist of a framework which is held together by chemical bonds or lattice energy. This framework carries a positive or negative electric surplus charge which is compensated by ions of opposite sign, the so-called counter ions. The counter ions are free to move within the framework and can be replaced by other ions of the same sign. The framework of a cation exchanger may be regarded as a macromolecular or crystalline polyanion, that of an anion exchanger as a polycation.

To give a very simple picture, the ion exchanger may be compared to a sponge with counter ions floating in the pores. When the sponge is immersed in a solution, the counter ions can leave the pores and float out. However, electroneutrality must be preserved, i.e., the electric surplus charge of the sponge must be compensated at any time by a stoichiometrically equivalent number of counter ions within the pores. Hence a counter ion can leave the sponge only when, simultaneously, another counter ion enters and takes over the task of contributing its share to the compensation of the framework charge.

With this “sponge” model at hand, he argues for that the reaction presented in eq. 2 above should be reformulated

[T]he model shows that ion exchange is essentially a statistical redistribution of counter ions between the pore liquid and the external solution, a process in which neither the framework nor the co-ions take part. Therefore Eqs. (1-1) [eq. 2 above] and (1-2) should be rewritten: \begin{equation} 2\overline{\mathrm{Na^+}} + \mathrm{Ca^{2+}} \leftrightarrow \overline{\mathrm{Ca^{2+}}} + 2\mathrm{Na^{+}} \end{equation} \begin{equation} 2\overline{\mathrm{Cl^-}} + \mathrm{SO_4^{2+}} \leftrightarrow \overline{\mathrm{SO_4^{2-}}} + 2\mathrm{Cl^{-}} \end{equation} Quantities with bars refer to the inside of the ion exchanger.

This “statistical redistribution” is of course nothing but the establishment of Donnan equilibrium between the external solution and the exchanger phase (as in the animation above). Naturally, Donnan equilibrium — using either the “classical” or the “new” equations — is at the heart of many analyses of ion exchange systems.

Unfortunately, this has not been the tradition in the compacted bentonite research field, where a “diffuse layer” approach to cation exchange has only been considered in more recent years, and then usually as a supplement to already existing models and tools. We are therefore in the rather uneasy situation that ion exchange in bentonite nowadays often is explained in terms of both a Donnan effect and as specific surface complexation.

Considering the robust evidence for significant ion mobility in interlayer pores, I strongly doubt surface complexation to be relevant for describing ion exchange in bentonite.¹¹ Instead, I believe that not separating these processes obscures the analysis of species that actually do sorb in these systems. In any event, the exact effects of Donnan equilibrium — a mechanism dependent on nothing but that some charges diffuses through the semi-permeable component, while some others don’t — must first and foremost be worked out.

A demonstration of compacted bentonite as a Donnan system

To demonstrate how well the Donnan effect in compacted bentonite is captured by Donnan’s original description, we use the following relation, derived from eq. 1 (i.e we assume only the presence of a 1:1 salt, apart from the impermeable component)

\begin{equation} \frac{c_\mathrm{Cl^-}^\mathrm{int}}{c_\mathrm{Cl^-}^\mathrm{ext}} = -\frac{1}{2}\frac{z}{c_\mathrm{Cl^-}^\mathrm{ext}} + \sqrt{\frac{1}{4} (\frac{z}{c_\mathrm{Cl^-}^\mathrm{ext}})^2+1} \tag{3} \end{equation}

Here \(z\) denotes the concentration of cations compensating impermeable charge. Eq. 3 quantifies anion exclusion, and is seen to depend only on the ratio \(c_\mathrm{Cl^-}^\mathrm{ext}/z\).

This equation is plotted in the diagram below, together with data of chloride exclusion in sodium dominated bentonite (Van Loon et al., 2007) and in potassium ferrocyanide (Donnan & Allmand, 1914)

Anion exclusion in bentonite and ferrocyanide compared with Donnan's ideal formula

I find this plot amazing. Although some points refer to bentonite at density 1900 \(\mathrm{kg/m^3}\) (corresponding to \(z \approx 5\) M), while others refer to a solution of approximately 25 mM \(\mathrm{K_4Fe(CN)_6}\) (\(z \approx 0.1\) M), the anion exclusion behavior is basically identical! Moreover, it fits the ideal “Donnan model” (eq. 3) quite well!

There is of course a lot more to be said about the detailed behavior of these systems, but I think a few things stand out:

It should be obvious that the basic mechanism for anion exclusion is the same in these two systems. This observed similarity thus invalidates the idea that anion exclusion in compacted bentonite is due to an intricate, ionic strength-dependent partitioning of a complex pore structure into parts which either are, or are not, accessible to chloride. In other words, the above plot is another demonstration that the concept of “accessible anion porosity” is nonsense.
The similarity between compacted bentonite and the simpler ferrocyanide system confirms Overbeek’s statement above, that Donnan’s “elementary” equations apply when the colloid concentration (i.e. density) is high enough.
The slope of the curve at small external concentrations directly reflects the amount of exchangeable cations that contributes to the Donnan effect. The similarity between model and experimental data thus confirms that the major part of the cations are mobile, i.e. not adsorbed by surface complexation. The similarity between the bentonite system and the ferrocyanide system also suggests that non-ideal corrections to the theory is better dealt with by means of e.g. activity coefficients, rather than by singling out a quite different mechanism (surface complexation) in one of the systems.

Footnotes

[1] The only equilibrium study of this kind I am aware of, that involves compacted, purified, homo-ionic clay, is Karnland et al. (2011). This study concerns Na/Ca exchange, and does not investigate the associated chloride equilibrium.

[2] I have assumed a K/Na selectivity coefficient of 2, and 95% salt exclusion.

[3] “Bentonite” is used in the following as an abbreviation for bentonite and claystone, or any clay system with significant cation exchange capacity.

[4] This particular publication states that I am one of the researchers using a “Donnan approach” to model “anion porosity”. Let me state for the record that I never have modeled “anion porosity”, or have any intentions to do so.

[5] This article has an English translation.

[6] In my head, a “soil suspension” and a “soil particle” are not very well defined entities. As I understand, Mattson investigated “Sharkey soil” and “Bentonite”. Sharkey soil is reported to have a cation exchange capacity of around 0.3 eq/kg, and the bentonite appear to be of “Wyoming” type. It is thus reasonably clear that Mattson’s “soil” particles are montmorillonite particles.

[7] Mattson and co-workers published a whole series of papers on “The laws of soil colloidal behavior” during the course of over 15 years, and appear to have caused both awe and confusion in the soil science community. I find it a bit amusing that there is a published paper (Kelley, 1943) which in turn reviews and comments on Mattson’s papers. Some statements in this paper include: “It seems to be generally agreed that some of [Mattsons papers] are difficult to understand.” and “The extensive use by [Mattson and co-workers] of terms either coined by them or used in new settings, the frequent contradictions of statement and inconsistencies in definition, and perhaps most important of all, the use by the authors of theoretical reasoning founded, not on experimentally determined data, but on calculations based on purely hypothetical premises, make it difficult to condense these papers into a form suitable for publication without doing injustice to the authors or sacrificing strict accuracy.”

[8] It may be worth noting that the only works referenced by Schofield — apart from a paper on dye adsorption — are Mattson, Procter and Donnan. Remarkably, Gouy is not referenced!

[9] Of course, one can instead solve the Poisson-Boltzmann equation for “overlapping” double layers.

[10] In its introduction is found the following gem: “A spectacular evolution began in 1935 with the discovery by two English chemists, Adams and Holmes, that crushed phonograph records exhibit ion-exchange properties.” Who wouldn’t want to hear more of that story?!

[11] As a further argument for that the concept of immobile exchangeable ions in bentonite is flawed, one can take a look at the spread in reported values for the fraction of such ions. You can basically find any value between \(>99\%\) and \(\sim 0\%\) for the same type of systems. To me, this indicates overparameterization rather than physical significance.

Swelling pressure, part III: osmosis

1 Reply

An established procedure in clay research is to differ between regions of “crystalline” and “osmotic” swelling. Although this distinction makes sense in many ways, I think it is unfortunate that one of the regions has been named “osmotic”, as it may suggest that bentonite¹ swelling is only partly osmotic, or that it is only osmotic in certain density ranges.

In this post I argue for that bentonite swelling pressure should be understood as an osmotic pressure under all conditions, and discuss the distinction between “crystalline” and “osmotic” swelling in some detail.

Bentonite swelling pressure is an osmotic pressure, under all conditions

A macroscopic definition of osmosis and osmotic pressure cannot depend on specific microscopic aspects. Here we take the description from Atkins’ Physical Chemistry² as a starting point

The phenomenon of osmosis is the spontaneous passage of a pure solvent into a solution separated from it by a semipermeable membrane , a membrane permeable to the solvent but not to the solute. The osmotic pressure , \(\Pi\), is the pressure that must be applied to the solution to stop the influx of solvent.

These definitions are written with simple aqueous solutions in mind,³ but can easily be generalized to include bentonite lab samples. For such a case the role of the “solution” is taken by the bentonite sample, and the “solutes” are the exchangeable cations and other dissolved species, as well as the individual clay particles. The semipermeable membrane in a bentonite set-up is typically filters confining the sample. Note that such filters are impermeable only to the clay particles, while e.g. the exchangeable ions can freely move across them. That the exchangeable ions anyway are located in the sample is because of the electrostatic coupling between them and the clay particles; the filters keep the clay particles in place, and the requirement of charge neutrality forces, in turn, the exchangeable ions to stay in place. Finally, in a bentonite set-up the external water source is in general itself an aqueous solution (often a salt solution). But even if the above description assumes a source of pure solvent it is clear that the mechanism (passage of solvent) is active also if the external source contains several components.

With these remarks it should be clear that water uptake in a laboratory bentonite sample is an osmotic effect and that swelling pressure is an osmotic pressure: swelling pressure is the pressure (difference) that must be applied to prevent further spontaneous inflow of water from the external source.

comparison conventional osmotic pressure and bentonite swelling pressure

Note that the definition of osmotic pressure says nothing about the specific microscopic conditions — it would be rather bizarre if it did. That would imply that the poor lab worker must have knowledge, e.g. of whether a certain interlayer distance is realized in the sample, in order to judge whether or not the measured swelling pressure is an osmotic pressure.

What qualifies swelling pressure as an osmotic pressure is summarized in the relation

\begin{equation} P_s = -\frac{\Delta \mu_w}{v}, \tag{1} \end{equation}

which in earlier blog posts was shown to be generally valid in bentonite. Here \(\Delta \mu_w\) is the difference in water chemical potential between the non-pressurized bentonite and the external solution, and \(v\) is the partial molar volume of water. The presence of \(\Delta \mu_w\) in eq. 1 expresses the “spontaneous” character of the phenomenon: “spontaneous” in this context means movement of water from higher to lower chemical potential. \(\Delta \mu_w\) may have contributions both from entropy and energy, which can be expressed (a bit sloppy) as

\begin{equation} \Delta \mu_w = \Delta h_w – T \Delta s_w, \tag{2} \end{equation}

where \(\Delta h_w\) and \(\Delta s_w\) are the differences in (partial) molar enthalpy and entropy, respectively, and \(T\) is the absolute temperature.

Indeed, \(\Delta h_w\) dominates in very dense bentonite. But the chemical potential having both energetic and entropic contributions is in principle no different from more conventional aqueous solutions, as manifested in osmotic coefficients generally being different from unity.

When only mixing entropy contributes to \(\Delta \mu_w\), and in the limit of a dilute solution, eq. 1 reduces to van ‘t Hoff’s formula \(\Pi = RTc\), where \(c\) is the solute concentration. Thus, rather than defining osmotic pressure, van ‘t Hoff’s formula is a limit of the the general relation expressed in eq. 1.

“Crystalline” vs. “osmotic” swelling

Although a division between “crystalline” and “osmotic” swelling regions can be found in the literature as far back as the 1930s, there doesn’t seem to be fully coherent definitions of these terms.

Some authors use an interlayer spacing range to define the crystalline swelling regions, some emphasize “hydration” of ions or surfaces (or both) as the defining feature. Some associate crystalline swelling with the release of an appreciable amount of heat, and others with that it occurs in discrete steps. There are also examples of authors differing between “limited” and “extensive” crystalline swelling.

Note that any of these definitions complies with swelling pressure being an osmotic pressure of the form discussed above; the release of heat, or effects of “hydration”, is accommodated by a non-zero enthalpy contribution (\(\Delta h_w\)) in eq. 2.

Also the “osmotic” swelling region is defined by some authors in terms of an interlayer spacing range. But in defining this region, many authors allude to some emerging “diffusive” property of the exchangeable cations, and here I really think the definitions become problematic. E.g. Madsen and Müller-Vonmoos (1989) discuss two “phases” of swelling, and write

Unlike innercrystalline swelling, which acts over small distances (up to 1 nm), osmotic swelling, which is based on the repulsion between electric double layers, can act over much larger distances. In sodium montmorillonite it can result in the complete separation of the layers. […] The driving force for the osmotic swelling is the large difference in concentration between the ions electrostatically held close to the clay surface and the ions in the pore water of the rock.

Leaving aside what is exactly meant by the term “pore water”, there are several issues here. Firstly, it appears that the authors have in mind a text book version of osmosis — basically van ‘t Hoff’s formula — when writing that the driving force is due to “differences in concentration”. But the actual driving force is differences in water chemical potential, which only under certain circumstances can be translated to differences in solute concentration. Note that also in the case of “crystalline” swelling is water transported from regions of low to regions of (really) high ion concentration. So, with the same logic you can also claim that the driving force for “crystalline” swelling is “large differences in concentration”.

Secondly, the electric double layer is an example of a system where there is no simple relation between ion concentration differences and transport driving forces — the diffuse layer displays an ion concentration gradient in equilibrium, and very weakly overlapping diffuse layers can be conceived of, where the driving force for in-transport of water is minimal, even though the ion concentration closest to the surfaces is large. To arrive at a van ‘t Hoff-like equation for the osmotic pressure of an overlapping diffuse layer, you first have to solve an electrostatic problem (the Poisson-Boltzmann equation, or something worse). With that analysis made, the (approximate⁴) osmotic pressure can be related to the midpoint concentration in the interlayer space. Madsen and Müller-Vonmoos (1989) present some electrostatic treatment, but, as far as I can see, don’t reflect over the amount of energetics involved in evaluating the osmotic pressure.

Lastly, the way these and many other authors single out the “diffusive” nature of the exchangeable cations when defining “osmotic” swelling implies that they do not consider ions to be diffusive in “crystalline” swelling states. Norrish (1954) states this quite explicitly (writing about the “crystalline” swelling region)

Nor can the interaction of diffuse double layers produce a repulsive force since in this region diffuse double layers are not formed. The repulsive forces of ion hydration and surface adsorption are probably the initial repulsive forces for many other colloids. They can cause surface separations of \(\sim 10\) Å, where the ions could begin to form diffuse double layers.

Even though I cannot find any explicit statements in Norrish (1954), writing like this makes me fear that authors of this era were under the impression that the initial interlayer hydration states consist of actual crystalline (non-liquid) water; I note that e.g. Grim (1953) has a several pages long section entitled “Evidence for the Crystalline State of the Initially Adsorbed Water”. Could it be that the original use of the term “crystalline” swelling was influenced by this belief?

Anyway, nowadays we have vast amount of evidence that interlayer water — at least down to the bihydrate — is liquid-like, and that ions in such states certainly diffuse. It follows that the osmotic pressure in such states has a contribution from mixing entropy.⁵ It should also be pointed out that the prevailing qualitative explanation for limited swelling in Ca-montmorillonite — which often is described as only displaying “crystalline” swelling — is due to ion-ion correlations in a diffusive system (“overlapping” diffuse layers).

Despite the evidence for interlayer diffusivity, it is very common to find descriptions in the bentonite literature that diffuse layers “develop” or “form” as the interlayers distances (or some other presumed pore) becomes large enough. This is usually claimed without giving a mechanism of how such a “development” or “formation” occurs. I genuinely wonder what authors using such descriptions believe the ions are doing when they have not “formed” a diffuse layer…

My message here is not that a division between “crystalline” and “osmotic” swelling should be discarded — for certain issues it makes a lot of sense to make a distinction, especially as the transition between these regions is not fully understood. But I think authors can do a better job in defining what exactly they mean by terms such as “osmotic”, “crystalline”, “diffusive”, etc. I furthermore wish that another name could be established for the “osmotic” swelling region (Norrish (1954) actually used “Region 1” and “Region 2”), although that seems rather unlikely. Until then we have to live with that bentonite swelling is described as “osmotic” only in a certain density range, while — if reasonable definitions are adopted — bentonite swelling pressure actually is an osmotic pressure under all conditions.

Footnotes

[1] In the following I usually mean bentonite when writing “bentonite”, even though the main points of the blog post also apply to claystone with swelling properties.

[2] The quotation is taken from the 8th edition.

[3] Note how this description does not refer to any microscopic concepts, nor to differences in concentrations. There seems to be a whole academic field devoted to sorting out misconceptions about osmosis. For further reading, I can recommend e.g. (Kramer and Mayer, 2012) and (Bowler, 2017).

[4] There may be additional significant activity corrections. I guess a solution of the Gouy-Chapman model could be compared to using the Debye-Hückel equation for a conventional aqueous salt solution.

[5] I am not arguing for that swelling is driven by entropy in these states — the entropy contribution is actually negative. But the entropy reasonably has both a positive (mixing) and a negative (hydration) part.

Evidence for anions in montmorillonite interlayers (swelling pressure, part II)

2 Replies

It is easy to find models assuming montmorillonite interlayers devoid of “anions” . Here I will present empirical evidence that such an assumption is incorrect. Before doing so, just a quick remark on the term “anions” in this context. If anions reside in interlayers, they certainly do so accompanied by excess cations, in order to maintain overall charge neutrality. Thus, when speaking of “anions” in the interlayer we really mean “salt” (= anion(s) + cation(s)). In the following I will use the term “salt” because it better reflects the overall charge neutral character of the process (we are not interested in pushing a handful of negative charge into an interlayer).

The nature of bentonite swelling

The evidence for salt having access to interlayers follows directly from the observed swelling pressure response to changes in external salinity. It is therefore important to first understand the thermodynamic basis for swelling pressure, which I wrote about in an earlier post (the same nomenclature is adopted here). In essence, swelling is a consequence of balancing the water chemical potential¹ in the clay with that in the external solution², and swelling pressure quantifies the difference in chemical potential between the external solution and the non-pressurized bentonite sample, as illustrated here

chemical potentials in non-pressurizied bentoniote and in external solution

Since the chemical potential in the external solution depends on the salt content, we generally expect a response in swelling pressure when altering external salinity.

Labeling the salt concentration \(c^{ext}\), we write the chemical potential of the external solution in terms of an osmotic pressure³

\begin{equation}
\mu_w^{ext} = \mu_0 – P_{osm.}^{ext}(c^{ext})\cdot v_w
\tag{1}
\end{equation}

where \(v_w\) is the partial molar volume of water. \(P_{osm}^{ext}\) is not the pressure in the external solution, but the pressure that would be required to keep the solution in equilibrium with pure water. The actual pressure in this compartment is the same as for the reference state: \(P_0\). It may seem confusing to use a “pressure” to specify the chemical potential, but we will see that it has its benefits. Experimentally we have full control of \(P_{osm}^{ext}\) by choosing an appropriate \(c^{ext}\).

Response in an indifferent clay

With salt in the external solution, the big question is what happens to the chemical potential of the clay. We will start by assuming (incorrectly) that external salt cannot access the interlayers. This means that the chemical potential of the (non-pressurized) bentonite does not change when the external salinity changes. We refer to this hypothetical bentonite as indifferent. In analogy with the external solution, we write the chemical potential of the indifferent non-pressurized bentonite as⁴ \begin{equation} \mu_w^{int}(P_0) = \mu_0 -P_s^0\cdot v_w \;\; \;\; \;\; \text{(indifferent clay)} \end{equation}

were \(P_s^0\) is the swelling pressure in case of pure water as external solution. By assumption, \(\mu_w^{int}(P_0)\) does not depend on the external salinity (it is independent of \(P_{osm}^{ext}\)). The chemical potential in the indifferent clay at an elevated pressure \(P\) is

\begin{equation}
\mu_w^{int}(P) = \mu_0 – P_s^0\cdot v_w +(P-P_0)\cdot v_w \;\;
\;\; \;\; \text{(indifferent clay)}
\tag{2}
\end{equation}

The swelling pressure (defined as the difference in pressure between bentonite and external solution, when the two are in equilibrium: \(P_s \equiv P_{eq} – P_0\)) in an indifferent clay is given by equating eqs. 1 and 2, giving the neat formula

\begin{equation}
P_s(c^{ext}) = P_s^0 – P_{osm}^{ext}(c^{ext}) \;\; \;\; \;\;
\text{(indifferent clay)}
\end{equation}

Note the following:

Although an indifferent clay is not affected by salt, it certainly has a swelling pressure response, demonstrating that swelling pressure depends as much on the external solution as it does on the clay.
Since swelling pressure in this case decreases linearly with the osmotic pressure of the external solution, it is predicted to vanish when the osmotic pressure equals \(P_s^0\).
External osmotic pressures larger than \(P_s^0\) implies “drying” of the clay (water transport from the clay into the external compartment)

If the above derivation feels a bit messy, with all the different types of pressure quantities to keep track of, here is a hopefully helpful animation

Animation swelling pressure response without anions in interlayer

Real swelling pressure response

Equipped with the swelling pressure response of an indifferent clay, let’s compare with the real response: The swelling pressure response in real bentonite deviates strongly from the indifferent clay response. This is seen e.g. here for Na-montmorillonite equilibrated in sequence with NaCl solutions of increasing concentration⁵ (data from Karnland et al., 2005 )

Swelling pressure response to salinities mid range densities

Swelling pressure indeed drops with increased concentration, but the drop is not linear in \(P^{ext}_{osm}\), and is weaker as compared with the indifferent clay response (shown by dashed lines). All samples in the diagram above exert swelling pressure when \(P^{ext}_{osm} \gg P_s^0\), i.e. far beyond the point where the swelling pressure in an indifferent clay is lost.

The deviation of the observed response from that of an indifferent clay directly demonstrates that the clay is affected by salt, i.e. that the chemical potential of the non-pressurized clay depends on the external salt concentration. The only reasonable way for salt to influence the chemical potential in the bentonite is of course to reside in the interlayer pores. Consequently, the observed swelling pressure response proves that salt from the external solution enters the interlayer pores.

Here is an illustration of how the chemical potentials relate to the swelling pressure in real bentonite

Swelling pressure repsonse real bentonite

Although the observed swelling pressure response in itself is sufficient to dismiss the idea that salt does not have access to interlayers, the study by Karnland et al., (2005) provides a much broader verification of the thermodynamic nature of swelling pressure. In particular, the chemical potential was measured (by means of vapor pressure) separately in the same samples as used for swelling pressure tests, after they had been isolated and unloaded. The terms in the relation \(P_s = \left(\mu_w^{ext} – \mu_w^{int}(P_0) \right)/v_w\) were thus checked independently, as indicated here

Measurements performed in Karnland et al. (2005)

A striking confirmation of salt residing in interlayers is given by the observation that the chemical potential in the non-pressurized samples is lower than that in the corresponding external solution, as well as that in non-pressurized samples of similar density, but equilibrated with pure water.

Another interesting observation is that the sample with the highest density behaves qualitatively similar to the others: although the external osmotic pressure never exceeded \(P_s^0\) (\(\approx\)56 MPa), the response strongly deviates from that of an indifferent clay

swelling pressure response to salinity high density

Because the pore space of samples this dense (\(2.02\;\mathrm{g/cm^3}\)) mainly consists of mono- and bihydrated interlayers, this similarity in response shows that salt has access also to such pores.

Implications

The issue of whether “anions” have access to montmorillonite interlayers has — for some reason — been a “hot” topic within the bentonite research community for a long time, and a majority of contemporary models rest on some version of the assumption that “anions” does not have access to the full pore volume. But, as far as I can see, this whole idea is based on misconceptions. I guess that saying so may sound quite grandiose, but note that swelling pressure is not at all considered in most chemical models of bentonite. And if it is, it is usually treated incorrectly. As an example, here is what Bradbury and Baeyens (2003) writes in a very influential publication

One of the main premises in the approach proposed here is that highly compacted bentonite can function as an efficient semi-permeable membrane (Horseman et al., 1996). This implies that the re-saturation of compacted bentonite involves predominantly the movement of water molecules and not solute molecules. Thus, to a first approximation, the composition of the external saturating aqueous phase should be a second-order effect which has little influence on the initial compacted bentonite porewater composition.
If the composition of the re-saturating water were to play an important role in determining the porewater composition, then it should also have a significant influence on swelling (Bolt, 1979). Dixon (2000) recently reviewed the role of salinity on the development of swelling pressure in bentonite buffer and backfill materials. He concluded that provided the initial dry densities were greater than 900 \(\mathrm{kg\;m^{-3}}\), the swelling pressures developed are unaffected for groundwater salinities \(< 75 \;\mathrm{g\;l^{-1}}\). Even brines appear to have little or no influence for initial dry densities \(>1500 \;\mathrm{kg\;m^{-3}}\).

But, as we just have learned, a system with a weak swelling pressure response necessarily has a significant contribution to its water chemical potential due to externally provided salt. In contrast, the approximation discussed in the first paragraph of the quotation — which is basically that of an indifferent clay — maximizes the swelling pressure response. Thus, the discussed “main premise” does not hold, and the provided empirical “support” is actually an argument for the opposite (i.e. that salt has access to the clay).

Footnotes

[1] In the following I will write only “chemical potential” — it is always the chemical potential of water that is referred to.

[2] This is just a complicated way of saying that swelling is (an effect of) osmosis.

[3] Some may say that \(P_{osm}^{ext}\) is simply the “suction” of the solution, but I am not a fan of using that concept in this context. I will comment on “suction” in a later blog post.

[4] The density dependence of the chemical potential in the bentonite is not explicitly stated here, in order to keep the formulas readable, but we assume throughout that the bentonite has some specific water-to-solid mass ratio \(w\).

[5] The NaCl concentrations are 0.0 M, 0.1 M, 0.3 M, 1.0 M, and 3.0 M.

Swelling pressure, part I

3 Replies

I am puzzled by how bentonite swelling pressure is presented in present day academic works.

In soil science, the thermodynamic description of the phenomenon has been around since at least the 1940s. Still, pure thermodynamic approaches to swelling pressure are not fashionable in modern day research. I think this is a pity, because for many issues this is the preferred approach.
Naturally, the notion of the Electric Double Layer (EDL) is central in many descriptions of bentonite swelling pressure, and EDL models seem to fit the bill very well for e.g. Li- and Na-montmorillonite at intermediate densities (at high density, the resulting pressure becomes increasingly sensitive to variations in model parameters, such as ionic radii). Models based on the EDL concept also give a satisfying qualitative explanation for the limited swelling of Ca- and Mg-montmorillonite, in terms of ion-ion correlation. But common EDL approaches — as far as I’m aware — fail to reproduce the observation that swelling pressure is significantly reduced in montmorillonites with heavier monovalent cations (e.g. K-montmorillonite).
Although the notion of an EDL captures essential parts of the observed swelling pressure behavior, it is nevertheless quite easy to find claims that e.g. DLVO theory has serious flaws , or even that the fundamental mechanism for clay swelling is not associated with the exchangeable cations¹. While many of these alternative descriptions may be easily (or not so easily) rejected, I fear that they have influenced a way of thinking about other aspects of bentonite, in particular the persistent idea of exchangeable cations as non-diffusive.
Modern geotechnical descriptions of bentonite often combine capillary concepts (surface tension, saturation,”suction” etc.) with a diffuse double layer mechanism. This seems conceptually incompatible, as a rigid structure — which is required to withstand attractive capillary forces — can hardly exist in a system that, under certain circumstances, is able to swell indefinitely.
In most geochemical treatments of bentonite, swelling pressure is simply ignored. This is remarkable as most modern reactive-transport models postulate different domains with different “types” of water, making the issue of water equilibrium critical.

Here, I would like to revisit the pure thermodynamic description of swelling pressure, which I think may help in resolving several misconceptions about swelling pressure.

Of course, thermodynamics cannot answer what the microscopic mechanism of swelling is, but puts focus on other — often relevant — aspects of the phenomenon. We thus take as input that, at the same pressure and temperature, the water chemical potential² is lowered in compacted bentonite as compared with pure water, and we ignore the (microscopic) reason for why this is the case. We write the chemical potential in non-pressurized³ bentonite as \begin{equation} \mu_w(w,P_0) = \mu_0 + \Delta \mu(w,P_0) \end{equation}

where \(\mu_0\) is a reference potential of pure bulk water at pressure \(P_0\) (isothermal conditions are assumed, and temperature will be left out of this discussion), and \(w\) is the water-to-solid mass ratio. Note that \(\Delta \mu(w,P_0)\) is a negative quantity.

The chemical potential in a pressurized system is given by integrating \(d\mu_w = v_wdP\), where \(v_w\) is the partial molar volume of water, giving⁴ \begin{equation} \mu_w(w,P) = \mu_0 + \Delta \mu(w,P_0) + v_w\cdot (P-P_0) \end{equation}

In order to define swelling pressure, we require that the bentonite is confined to a certain volume while still having access to externally supplied water, i.e. that it is separated from an external water source by a semi-permeable component. This may sound abstract, but is in fact how any type of swelling pressure test is set up: water is supplied to the sample via e.g. sintered metal filters.

With this boundary condition, a relation between swelling pressure and the chemical potential is easily obtained by invoking the condition that, at equilibrium, the chemical potential is the same everywhere. Assuming an external reservoir of pure water at pressure \(P_0\), its chemical potential is \(\mu_0\), and the equilibrium condition reads \begin{equation} \mu_w(w,P_{eq}) = \mu_0 + \Delta \mu(w,P_0) + v_w\cdot (P_{eq}-P_0) = \mu_0 \end{equation}

where \(P_{eq}\) is the pressure in the bentonite at thermodynamic equilibrium.

Defining the swelling pressure as \(P_s = P_{eq}-P_0\) we get the desired relation⁵ \begin{equation} P_s = -\frac{\Delta \mu(w,P_0)}{v_w} \tag{4} \end{equation}

Alternatively this relation can be expressed in terms of activity (related to the chemical potential as \(\mu = \mu_0 +RT\ln a\)) \begin{equation} P_s = -\frac{RT}{v_w}\ln a (w,P_0) \tag{5} \end{equation}

or, if the activity is expressed in terms of the vapor pressure, \(P_v\), in equilibrium with the sample, \begin{equation} P_s = -\frac{RT}{v_w}\ln \frac{P_v}{P_{v0}} \tag{6} \end{equation}

where \(P_{v0}\) is the corresponding vapor pressure of pure bulk water.

The above relation has been presented in the literature for a long time. But, as far as I am aware, direct interpretation of experimental data using eq. 4 is more scarce. Spostio (72) compares swelling pressures in Na-montmorillonite (reported by Warkentin et al 57) with water activities measured in the materials (reported by Klute and Richards 62) and concludes a “quite satisfactory” agreement of eq. 4 (the highest pressures were on the order of 1 MPa). He moreover comments

Future measurements of \(P_S\) and \(\Delta \mu_w\) for pure clays and soils as a function of water content would do much to help assess the merit of equation (11) [eq. 4 here].

Such “future” measurements were indeed presented by Bucher et al (1989), for “natural” bentonites in a density range including very high pressures (\(\sim 40\) Mpa). For “MX-80” the data looks like this

Here the value of \(v_w\) was set equal to the molar volume of bulk water when applying eq. 6. It is interesting to note that this value, which is necessarily correct in the limit of low density, appears to be valid for densities as large as \(2\;\mathrm{g/cm^3}\).

The clearest demonstration of the validity of eq. 4 is in my opinion the study by Karnland et al. (2005), where swelling pressure and vapor pressure were measured on the same samples. The result for Na-montmorillonite is shown below (again, the value of bulk water molar volume was used for \(v_w\)).

The above plots make it clear that the description underlying eq. 4 (or eq. 5, or eq. 6) is valid for bentonite, at any density. An important consequence of this insight — and something I think is often not emphasized enough — is that swelling pressure depends as much on the external solution as it does on the bentonite.

Measuring the response in swelling pressure to changes in the external solution is therefore a powerful method for exploring the physico-chemical behavior of bentonite. I will return to this point in later blog posts, in particular when discussing the “controversial” issue whether “anions” have access to montmorillonite interlayers.

The animation below summarizes the thermodynamic view of the development of swelling pressure: the external reservoir fixes the value of the water chemical potential, and in order for the bentonite sample to attain this level, its pressure increases.

Footnotes

[1] You can even find a statement saying that clay swelling has been proved to be “due to long-range interaction between particle surfaces and the water” (I don’t agree).

[2] In the following I will simply write “chemical potential”. Here the water chemical potential is the only one involved.

[3] Here “non-pressurized” means being at the reference pressure \(P_0\). In practice \(P_0\) is usually atmospheric absolute pressure.

[4] Here it is assumed that \(v_w\) is independent of pressure. Also, using \(w\) as thermodynamic variable implies that the water chemical potential is measured in units of energy per mass, which requires this volume factor to be the partial specific volume of water. Here we assume that the chemical potential is measured in units energy per mol, but use \(w\) for quantifying the amount of water in the clay, since it is the more commonly used variable in the bentonite world. The amount of moles of water is of course in strict one-to-one correspondence with the water mass.

[5] What is said here is that swelling pressure generally is identified as an osmotic pressure. I will expand on this in a future blog post.