We have discussed various aspects of “anion exclusion” on this blog. This concept is often used to justify multi-porosity models of compacted bentonite, by reasoning that the exclusion mechanism makes parts of the pore space inaccessible to anions. But we have seen that this reasoning has no theoretical backing: studies making such assumptions usually turn out to refer to conventional electric double layer theory, described e.g. by the Poisson-Boltzmann equation. In the following, we refer to the notion of compartments inaccessible to anions as complete anion exclusion.

In fact, a single, physically reasonable concept underlies basically all descriptions of anion exclusion in the clay literature: charge separation. Although the required mathematics may differ for different systems — may it be using Donnan’s “classical equations”, or the Poisson-Boltzmann equation — the underlying mechanism is the same. In the following we refer to this type of description as traditional theory or Donnan theory. It is important to recognize that traditional theory is incompatible with complete anion exclusion: the Poisson-Boltzmann equation predicts anions everywhere.

In more recent years, however, a different meaning of the term “anion exclusion” has sneaked into the literature. This seems to be related to the dawn of molecular dynamics (MD) simulations of clays. In particular, the study of Rotenberg et al. (2007) — which I think is the first published MD simulation of montmorillonite interlayers in contact with an external compartment — is frequently cited as demonstrating qualitatively different results as compared with the traditional models. E.g. Kosakowski and Berner (2013) write

Very often it is assumed that negatively charged ions are strongly hindered to enter the interlayer space (Kosakowski et al., 2008; Rotenberg et al., 2007), although other authors come to different conclusions (Karnland et al., 2007). Note that we favor the former view with our montmorillonite setup.

Although the terms “assumed” and “conclusions” seem misplaced, it is clear that Kosakowski and Berner (2013) mean that the interlayer space is essentially anion-free, rather than obeying ordinary Donnan equilibrium (the approach used in Karnland et al. (2007)).

A similar citation is found in Tournassat and Steefel (2015)

The interlayer space can be seen as an extreme case where the diffuse layer vanishes leaving only the Stern layer of the adjacent basal surfaces. For this reason, the interlayer space is often considered to be completely free of anions (Tournassat and Appelo 2011), although this hypothesis is still controversial (Rotenberg et al. 2007c; Birgersson and Karnland 2009).

Here Tournassat and Steefel (2015) conceive of the interlayer space as something distinctly different from a diffuse layer,¹ and they mean that the MD result stands in contrast to conventional Donnan theory (Birgersson and Karnland, (2009)).

As a third example, Wersin et al. (2016) write

Based upon [results from anion diffusion tests], anion-exclusion models have been formulated, which subdivide the water-filled pore space into interlayer, diffuse (or electric) double layer (DDL) and “free” water porosities (Wersin et al. 2004; Tournassat & Appelo 2011; Appelo 2013). In this formulation, anions are considered to reside in the “free” electrically neutral solution and in the DDL in the external (intergranular) pores, whereas the interlayer (intragranular) space is considered devoid of anions. Support for this model has been given by molecular dynamics simulations (Rotenberg et al. 2007), but this issue remains controversial (Birgersson & Karnland 2009)

The term “anion-exclusion” is here fully transformed to refer to complete exclusion, rather than to the traditional theory from which the term was coined. Note that the picture of bentonite given in this and the previous quotations is basically the contemporary mainstream view, which we discussed in a previous blog post. This description has not emerged from considering MD results that are allegedly in contradiction with traditional Donnan equilibrium theory. Rather, it has resulted from misusing the concept of exclusion-volume. The study of Rotenberg et al. (2007) (Rot07, in the following) supports the contemporary mainstream view only to the extent that it is at odds with the predictions of traditional theory. But is it? Let’s take a look at the relevant MD studies.

Rotenberg et al. (2007)

Rot07 is not primarily a study of the anion equilibrium, but considers more generally the transition of species between an external compartment² and interlayer pores: water, cations (Na and Cs), and anions (Cl). The study only concerns interlayers with two monolayers of water, in the following referred to as a 2WL system. There is of course nothing wrong with exclusively studying the 2WL system, but this study alone cannot be used to support general model assumptions regarding interlayers (which anyway is commonplace, as we saw above). The meaning of the term “interlayer” in modern clay literature is quite confusing, but there is at least full consensus that it includes also states with three monolayers of water (3WL) (we’ll get back to those). Rot07 furthermore consider only a single external concentration, of 0.52 M.

Here is an illustration of the simulated system:

A cell (outlined with dashed lines) containing two montmorillonite layers (yellow) and six chloride ions (green) is repeated infinitely in all directions (the cell depth in the direction normal to the picture is 20.72 Å). While only chloride ions are indicated in this figure, also cations, water atoms, and montmorillonite atoms are explicitly accounted for in the simulation.

Note that the study neither varies density (interlayer distance) nor external concentration (number of chloride ions) — two variables essential for studying anion equilibrium. I don’t mean this as direct criticism, but it should be recognized when the study is used to support assumptions regarding interlayers in other models.

What I do want to criticize, however, is that Rot07 don’t actually compare with Donnan theory. Instead, they seem to be under the impression that traditional theory predicts complete exclusion in their system. Consider this passage in the introduction

Due to the negative charge of clay layers, anions should be repelled by the external surfaces, and excluded from the interlayers. On the contrary, cations are attracted by the surfaces, and may exchange with the natural interlayer counterions.

Here they associate two different terms with the anions: they are repelled by the “external surfaces” and excluded from “interlayers”. I can only interpret this as meaning that anions are completely excluded from interlayers, especially as the wording “on the contrary” is used when describing cations.³

The study comprises both a “plain” MD simulation of the (presumed) equilibrium state, and separate calculations of free energy profiles. In the “plain” MD simulation, anions do not enter the interlayers, and the calculation of the free energy profile gives a barrier of ~9 kT for chloride to enter the interlayer.

These results motivate the authors to conclude that the “thermal fluctuations do not allow anions to overcome the free energy barrier corresponding to their entrance into the interlayer” and that “anions are excluded from the interlayer: the probability for an anion reaching the interface to enter into the interlayer is very small (of the order of e^-9 ~ 10^-4)”

It is important to keep in mind that the authors are under the impression that this result and conclusion are in line with the traditional description of anion exclusion.³ When summarizing their findings they write

All the results are in agreement with the common sense on ionic exchange and anion exclusion.

and

The results confirm the generally admitted ideas of ionic exchange and anion exclusion

The problem is that this “common sense” and these “generally admitted ideas” are based on misconceptions of traditional theory (I also think one should be careful with using terms like these in scientific writing). Consequently, the authors erroneously conclude that their results confirm, rather than contrast, traditional theory. This is opposite to how this study is referred to in later publications, as was exemplified above.

The anion exclusion predicted from Donnan theory for the system in Rot07 is estimated as follows. The adopted montmorillonite unit cell (Na_0.75Si₈Al_3.25Mg_0.75O₂₀OH₄) has structural charge 0.75e, and lateral dimensions 8.97 Å × 5.18 Å. With an interlayer width of 6.1 Å we thus have for the concentration of interlayer charge

\begin{equation} c_{IL} = \frac{0.75/N_A}{8.97\cdot 5.18\cdot 6.1 \mathrm{Å^3}} = 4.39 \;\mathrm{M} \end{equation}

where \(N_A\) is the Avogadro constant. Using this value for \(c_{IL}\) in the expression for internal anion concentration in an ideal 1:1 Donnan system,

\begin{equation} c^\mathrm{int} = \frac{c_{IL}}{2} \left ( \sqrt{1+\frac{4\cdot (c^\mathrm{ext})^2}{c_{IL}^2}} – 1 \right ) \tag{1} \end{equation}

together with \(c^\mathrm{ext}\) = 0.52 M, gives

\begin{equation} c^\mathrm{int} = 0.06 \;\mathrm{M} \end{equation}

This should be the anion interlayer concentration expected from “generally admitted ideas”, and Rot07 should have concluded that their results differ by a factor ~1000 (or more) from traditional theory. This is not to say that the calculations are incorrect (more on that later), but it certainly puts the results in a different light. A discrepancy of this magnitude should reasonably be of interest to investigate further.

Hsiao and Hedström (2015)

Considerably more detailed MD simulations of the 2WL system are provided by Hsiao and Hedström (2015) (Hsi15, hereafter). In contrast to Rot07, Hsi15 specifically focus on the anion equilibrium, and they explicitly compare with both conventional Donnan theory, and the results of Rot07. In these simulations, chloride actually populates the interlayer.

Hsi15 also analyze the convergence behavior, by varying system size and simulation time. This analysis makes it clear both that most of the simulations presented in the paper are properly converged, and that the simulation of Rot07 is not. With external concentration 1.67 M, Hsi15 demonstrate that, during intervals of 20 ns, the interlayer concentration fluctuates between basically zero and 0.13 M (converged value: 0.04 M), in a system with similar size as that of Rot07. Given that the total simulation time of the earlier study is 20 ns, and that it also adopts a considerably lower external concentration, its result of zero chloride concentration in the interlayer is no surprise.

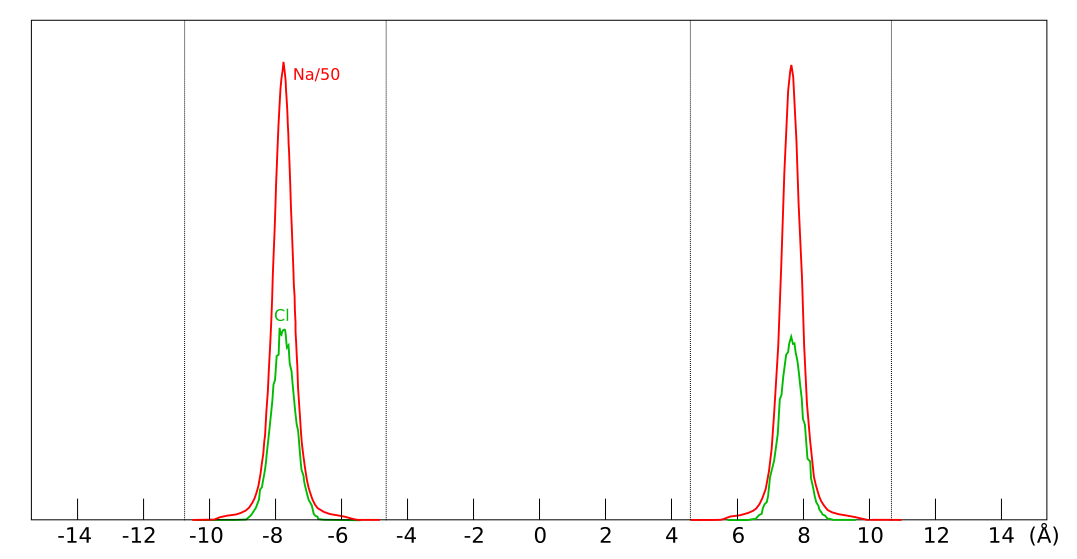
The converged interlayer concentrations in Hsi15 look like this in the direction normal to the basal surfaces (simulation time: 150 ns, layer size: 8 × 4 unit cells, external concentration: 1.67 M)

Note that the simulation contains two interlayer pores (indicated by the dotted lines; cf. the illustration of the simulated system) and that sodium and chloride populate the same central layer, sandwiched by the two water layers (not shown). The nearly identical chloride profiles are a strong confirmation that the simulation is converged.

The chloride interlayer concentrations evaluated in Hsi15 deviate strongly from the predictions of the ideal Donnan formula. With \(c_{IL}\) = 4.23 M (as reported in the article) and \(c^\mathrm{ext}\) = 1.67 M, eq. 1 gives \(c^\mathrm{int}\) = 0.580 M, while the MD results are in the range 0.033 M — 0.045 M, i.e. more than a factor 10 lower (but not a factor 1000).

Hsi15 also calculate the free energy profiles along the coordinate connecting the external compartment and the interlayer, similar to the technique utilized by Rot07 (as far as I understand). For the external concentration of 1.67 M they evaluate a free energy barrier of ~3.84 kT, which corresponds to an interlayer concentration of 0.036 M, and is in good agreement with the directly evaluated concentrations.

Note that Hsi15 — in contrast to Rot07 — conclude significant deviation between the MD results of the 2WL system and ideal traditional theory. Continuing their investigation (again, in contrast to Rot07), Hsi15 found that the contribution from ion hydration to the free energy barrier basically make up for the entire discrepancy with the ideal Donnan formula. Moreover, even though the ideal Donnan formula strongly overestimates the actual values obtained from MD, it still shows the correct dependency on external concentration: when the external concentration is lowered to 0.55 M, the evaluated free energy barrier increases to ~5.16 kT, which corresponds to a reduction of the internal concentration by about a factor of 10. This is in agreement with Donnan theory, which gives for the expected reduction (0.55/1.67)² ≈ 0.11.

From the results of Hsi15 (and Rot07, for that matter), a relatively clear picture emerges: MD simulated 2WL systems function as Donnan systems. Anions are not completely excluded, and the dependency on external concentration is in line with what we expect from a varying Donnan potential across the interface between interlayer and external compartment (Hsi15 even comment on observing the space-charge region!).

The simulated 2WL system is, however, strongly non-ideal, as a consequence of the ions not being optimally hydrated. Hsi15 remark that the simulations probably overestimate this energy cost, e.g. because atoms are treated as non-polarizable. This warning should certainly be seriously considered before using the results of MD simulated 2WL systems to motivate multi-porosity in compacted bentonite. But, concerning assumptions of complete anion exclusion in interlayers, another system must obviously also be considered: 3WL.

Hedström and Karnland (2012)

MD simulations of anion equilibrium in the 3WL system are presented in Hedström and Karnland (2012) (Hed12, in the following). Hed12 consider three different external concentrations, by including either 12, 6, or 4 pairs of excess ions (Cl^– + Na⁺). This study also varies the way the interlayer charge is distributed, by either locating unit charges on specific magnesium atoms in the montmorillonite structure, or by evenly reducing the charge by a minor amount on all the octahedrally coordinated atoms.

Here are the resulting ion concentration profiles across the interlayer, for the simulation containing 12 chloride ions, and evenly distributed interlayer charge (simulation time: 20 ns, layer size: 4 × 4 unit cells)

Chloride mainly resides in the middle of the interlayer also in the 3WL system, but is now separated from sodium, which forms two off-center main layers. The dotted lines indicate the extension of the interlayer.

The main objectives of this study are to simply establish that anions in MD equilibrium simulations do populate interlayers, and to discuss the influence of unavoidable finite-size effects (6 and 12 are, after all, quite far from Avogadro’s number). In doing so, Hed12 demonstrate that the system obeys the principles of Donnan equilibrium, and behaves approximately in accordance with the ideal Donnan formula (eq. 1). The authors acknowledge, however, that full quantitative comparison with Donnan theory would require better convergence of the simulations (the convergence analysis was further developed in Hsi15). If we anyway make such a comparison, it looks like this

#Cl TOT	Layer charge	#Cl IL	\(c^\mathrm{ext}\)	\(c^\mathrm{int}\) (Donnan)	\(c^\mathrm{int}\) (MD)
12	distr.	1.8	1.45	0.62	0.42 (67%)
12	loc.	1.4	1.50	0.66	0.32 (49%)
6	distr.	0.6	0.77	0.20	0.14 (70%)
6	loc.	1.3	0.67	0.15	0.30 (197%)
4	distr.	0.2	0.54	0.10	0.05 (46%)
4	loc.	0.18	0.54	0.10	0.04 (41%)

The first column lists the total number of chloride ions in the simulations, and the second indicates if the layer charge was distributed on all octahedrally coordinated atoms (“distr.”) or localized on specific atoms (“loc.”) The third column lists the average number of chloride ions found in the interlayer in each simulation. \(c^\mathrm{ext}\) denotes the corresponding average molar concentration in the external compartment. The last two columns lists the corresponding average interlayer concentration as evaluated either from the Donnan formula (eq. 1 with \(c_{IL}\) = 2.77 M, and the listed \(c^\mathrm{ext}\)), or from the simulation itself.

The simulated results are indeed within about a factor of 2 from the predictions of ideal Donnan theory, but they also show a certain variation in systems with the same number of total chloride ions,⁴ indicating incomplete convergence (compare with the fully converged result of Hsi15). It is also clear from the analysis in Hed12 and Hsi15 that the simulations with the highest number of chloride ions (12) are closer to being fully converged.⁵ Let’s therefore use the result of those simulations to compare with experimental data.

Comparison with experiments

In an earlier blog post, we looked at the available experimental data on chloride equilibrium concentrations in Na-dominated bentonite. Adding the high concentration chloride equilibrium results from Hed12 and Hsi15 to this data (in terms of \(c^\mathrm{int}/c^\mathrm{ext}\)), gives the following picture⁶ (the 3WL system corresponds to pure montmorillonite of density ~1300 kg/m³, and the 2WL system corresponds to ~1600 kg/m³, as also verified experimentally).

The x-axis shows montmorillonite effective dry density, and applied external concentrations for each data series are color coded, but also listed in the legend. Note that this plot contains mainly all available information for drawing conclusions regarding anion exclusion in interlayers.⁷ To me, the conclusions that can be drawn are to a large extent opposite to those that have been drawn:

• The amount chloride in the simulated 3WL system corresponds roughly to measured values. Consequently, MD simulations do not support models that completely exclude anions from interlayers.
• The 3WL results instead suggest that interlayers contain the main contribution of chloride. Interlayers must consequently be handled no matter how many additional pore structures a model contains.
• For systems corresponding to 2WL interlayers, there is a choice: Either,
  1. assume that the discrepancy between simulations and measurements indicates the existence of an additional pore structure, where the majority of chloride resides, or
  2. assume that presently available MD simulations of 2WL systems overestimate “anion” exclusion.⁸
• If making choice no. 1. above, keep in mind that the additional pore structure cannot be 3WL interlayers (they are virtually non-existent at 1600 kg/m³), and that it should account for approximately 0% of the pore volume.

Tournassat et al. (2016)

Tournassat et al. (2016) (Tou16, in the following) present more MD simulations of interlayer pores in contact with an external compartment, with a fixed amount of excess ions, at three different interlayer distances: 2WL (external concentration ~0.5 M), 3WL (~0.4 M), and 5WL (~0.3 M).

In the 2WL simulations, no anions enter the interlayers. Tou16 do not reflect on the possibility that 2WL simulations may overestimate exclusion, as suggested by Hsi15,⁹ but instead use this result to argue that anions are basically completely excluded from 2WL interlayers. They even imply that the result of Rot07 is more adequate than that of Hsi15

In the case of the 2WL hydrate, no Cl^– ion entered the interlayer space during the course of the simulation, in agreement with the modeling results of Rotenberg et al. (2007b), but in disagreement with those of Hsiao and Hedström (2015).

But, as discussed, there is no real “disagreement” between the results of Hsi15 and Rot07. To refute the conclusions of Hsi15, Tou16 are required to demonstrate well converged results, and analyze what is supposedly wrong with the simulations of Hsi15. It is, furthermore, glaringly obvious that most of the anion equilibrium results in Tou16 are not converged.

Regarding convergence, the only “analysis” provided is the following passage

The simulations were carried out at the same temperature (350 K) as the simulations of Hsiao and Hedström (2015) and with similar simulation times (50 ns vs. 100-200 ns) and volumes (27 × 10⁴ ų vs. 15 × 10⁴ ų), thus ensuring roughly equally reliable output statistics. The fact that Cl^– ions did not enter the interlayer space cannot, therefore, be attributed to a lack of convergence in the present simulation, as Hsiao and Hedström have postulated to explain the difference between their results and those of Rotenberg et al. (2007b).

I mean that this is not a suitable procedure in a scientific publication — the authors should of course demonstrate convergence of the simulations actually performed! (Especially after Hsi15 have provided methods for such an analysis.¹⁰)

Anyhow, Tou16 completely miss that Hsi15 demonstrate convergence in simulations with external concentration 1.67 M; for the system relevant here (0.55 M), Hsi15 explicitly write that the same level of convergence requires a 10-fold increase of the simulation time (because the interlayer concentration decreases approximately by a factor of 10, as predicted by — Donnan theory). Thus, the simulation time of Tou16 (53 ns) should be compared with 2000 ns, i.e. it is only a few percent of the time required for proper convergence.

Further confirmation that the simulations in Tou16 are not converged is given by the data for the systems where chloride has entered the interlayers. The ion concentration profiles for the 3WL simulation look like this

The extension of the interlayers is indicated by the dotted lines. Each interlayer was given slightly different (average) surface charge density, which is denoted in the figure. One of the conspicuous features of this plot is the huge difference in chloride content between different interlayers: the concentration in the mid-pore (0.035 M) is more than three times that in left pore (0.010 M). This clearly demonstrates that the simulation is not converged (cf. the converged chloride result of Hsi15). Note further that the larger amount of chloride is located in the interlayer with the highest surface charge, and the least amount is located in the interlayer with the smallest surface charge.¹¹ I think it is a bit embarrassing for Clays and Clay Minerals to have used this plot for the cover page.

As the simulation times (53 ns vs. 40 ns), as well as the external concentrations (~0.5 M vs. ~0.4 M), are similar in the 2WL and and 3WL simulations, it follows from the fact that the 3WL system is not converged, that neither is the 2WL system. In fact, the 2WL system is much less converged, given the considerably lower expected interlayer concentration. This conclusion is fully in line with the above consideration of convergence times in Hsi15.

For chloride in the 3WL (and 5WL) system, Tou16 conclude that “reasonable quantitative agreement was found” between MD and traditional theory, without the slightest mentioning of what that implies.¹² I find this even more troublesome than the lack of convergence. If the authors mean that MD simulations reveal the true nature of anion equilibrium (as they do when discussing 2WL), they here pull the rug out from under the entire mainstream bentonite view! With the 3WL system containing a main contribution, interlayers can of course not be modeled as anion-free, as we discussed above. Yet, not a word is said about this in Tou16.

In this blog post I have tried to show that available MD simulations do not, in any reasonable sense, support the assumption that anions are completely excluded from interlayers. Frankly, I see this way of referencing MD studies mainly as an “afterthought”, in attempts to justify the misuse of the exclusion-volume concept. In this light, I am not surprised that Hed12 and Hsi15 have not gained reasonable attention, while Tou16 nowadays can be found referenced to support claims that anions do not have access to “interlayers”.¹³

Footnotes

[1] I should definitely discuss the “Stern layer” in a future blog post. Update (250113): Stern layers are discussed here.

[2] The view of bentonite (“clay”) in Rotenberg et al. (2007) is strongly rooted in a “stack” concept. What I refer to as an “external compartment” in their simulation, they actually conceive of as a part of the bentonite structure, calling it a “micropore”.

[3] That Rotenberg et al. (2007) expresses this view of anion exclusion puzzles me somewhat, since several of the same authors published a study just a few years later where Donnan theory was explored in similar systems: Jardat et al. (2009).

[4] Since the number of chloride ions found in the interlayer is not correlated with how layer charge is distributed, we can conclude that the latter parameter is not important for the process.

[5] The small difference in the two simulations with 4 chloride ions is thus a coincidence.

[6] I am in the process of assessing the experimental data, and hope to be able to better sort out which of these data series are more relevant. So far I have only looked at — and discarded — the study by Muurinen et al. (1988). This study is therefore removed from the plot.

[7] There are of course several other results that indirectly demonstrate the presence of anions in interlayers. Anyway, I think that the bentonite research community, by now, should have managed to produce better concentration data than this (both simulated and measured).

[8] As the cation (sodium) may give a major contribution to the hydration energy barrier (this is not resolved in Hsiao and Hedström (2015)), it may be inappropriate to refer to this part as “anion” exclusion (remember that it is salt that is excluded from bentonite). It may be noted that sodium actually appear to have a hydration barrier in e.g. the Na/Cs exchange process, which has been explored both experimentally and in MD simulations.

[9] Tournassat et al. (2016) even refer to Hsiao and Hedström (2015) as presenting a “hypothesis” that “differences in solvation energy play an important role in inhibiting the entry of Cl^– in the interlayer space”, rather than addressing their expressed concern that the hydration energy cost may be overestimated.

[10] Ironically, Tournassat et al. (2016) choose to “rely” on the convergence analysis in Hsiao and Hedström (2015), while simultaneously implying that the study is inadequate.

[11] As the interlayers have different surface charge, they are not expected to have identical chloride content. But the chloride content should reasonably decrease with increasing surface charge, and the difference between interlayers should be relatively small.

[12] Here we have to disregard that the “agreement” is not quantitative. It is not even qualitative: the highest chloride content was recorded in the interlayer pore with highest charge, in both the 3WL and the 5WL system.

[13] There are even examples of Hedström and Karnland (2012) being cited to support complete exclusion!