In the ongoing assessment of chloride equilibrium concentrations in bentonite, we here take a closer look at the study by Molera et al. (2003), in the following referred to as Mo03. We thus assess the 13 points indicated here
Mo03 performed both chloride and iodide through-diffusion tests on “MX-80” bentonite, but here we focus on the chloride results. However, since the only example in the paper of an outflux evolution and corresponding concentration profile is for iodide, this particular result will also be investigated. The tests were performed at background concentrations of 0.01 M or 0.1 M NaClO4, and nominal sample densities of 0.4, 0.8, 1.2, 1.6, and 1.8 g/cm3. We refer to a single test by stating “nominal density/background concentration”, e.g. a test performed at nominal density 1.6 and background concentration 0.1 M is referred to as “1.6/0.1”.
Uncertainty of samples
The material used is discussed only briefly, and the only reference given for its properties is (Müller-Von Moos and Kahr, 1983). I don’t find any reason to believe that the “MX-80” batch used in this study actually is the one investigated in this reference, and have to assume the same type of uncertainty regarding the material as we did in the assessment of Muurinen et al (1988). I therefore refer to that blog post for a discussion on uncertainty in montmorillonite content, cation population, and soluble calcium minerals.
Density
The samples in Mo03 are cylindrical with radius 0.5 cm and length 0.5 cm, giving a volume of 0.39 cm3. This is quite small, and corresponds e.g. only to about 4% of the sample size used in Muurinen et al (1988). With such a small volume, the samples are at the limit for being considered as a homogeneous material, especially for the lowest densities: the samples of density 0.4 g/cm3 contain 0.157 g dry substance in total, while a single 1 mm3 accessory grain weighs about 0.002 — 0.003 g.
Furthermore, as the samples are sectioned after termination, the amount substance in each piece may be very small. This could cause additional problems, e.g. enhancing the effect of drying. The reported profile (1.6/0.1, iodide diffusion) has 10 sections in the first 2 mm. As the total mass dry substance in this sample is 0.628 g, these sections have about 0.025 g dry substance each (corresponding to the mass of about ten 1 mm3 grains). For the lowest density, a similar sectioning corresponds to slices of dry mass 0.006 g (the paper does not give any information on how the low density samples were sectioned).
Mo03 only report nominal densities for the samples, but from the above considerations it is clear that a substantial (but unknown) variation may be expected in densities and concentrations.
A common feature of many through-diffusion studies is that the sample density appears to decrease in the first few millimeters near the confining filters. We saw this effect in the profiles of Muurinen et al (1988), and it has been the topic of some studies, including Mo03. Here, we don’t consider any possible cause, but simply note that the samples seem to show this feature quite generally (below we discuss how Mo03 handle this). Since the samples of Mo03 are only of length 5 mm, we may expect that the major part of them are affected by this effect. Of course, this increases the uncertainty of the actual density of the used samples.
Uncertainty of external solutions
Mo03 do not describe how the external solutions were prepared, other than that they used high grade chemicals. We assume here that the preparation did not introduce any significant uncertainty.
Since “MX-80” contains a substantial amount of divalent ions, connecting this material with (initially) pure sodium solutions inevitably initiates cation exchange processes. The extent of this exchange depends on details such as solution concentrations, reservoir volumes, number of solution replacements, time, etc…
Very little information is given on the volume of the external solution reservoirs. It is only hinted that the outlet reservoir may be 25 ml, and for the inlet reservoir the only information is
The volume of the inlet reservoir was sufficient to keep the concentration nearly constant (within a few percent) throughout the experiments.
Consequently, we do not have enough information to assess the exact ion population during the course of the tests. We can, however, simulate this process of “unintentional exchange” to get some appreciation for the amount of divalent ions still left in the sample, as we did in the assessment of Muurinen et al. (1988). Here are the results from calculating the exchange equilibrium between a sample initially containing 30% exchangeable charge in form of calcium (70% sodium), and external NaClO4 solutions of various concentrations and volumes
In these calculations we assume a sample of density 1.6 g/cm3 (except when indicated), a volume of 0.39 cm3, a cation exchange capacity of 0.75 eq/kg, and a Ca/Na selectivity coefficient of 5.
These simulations make it clear that the tests performed at 0.01 M most probably contain most of the divalent ions initially present in the “MX-80” material: even with an external solution volume of 1000 ml, or with density 0.4 g/cm3, exchange is quite limited. For the tests performed at 0.1 M we expect some exchange of the divalent ions, but we really can’t tell to what extent, as the exact value strongly depends on handling (solution volumes, if solutions were replaced, etc.). That the exact ion population is unknown, and that the divalent/monovalent ratio probably is different for different samples, are obviously major problems of the study (the same problems were identified in Muurinen et al (1988)).
Uncertainty of diffusion parameters
Diffusion model
Mo03 determine diffusion parameters by fitting a model to all available data, i.e the outflux evolution and the concentration profile across the sample at termination. The model is solved by a numerical code (“ANADIFF”) that takes into account transport both in clay samples and filters. The fitted parameters are an apparent diffusivity, \(D_a\), and a so-called “capacity factor”, \(\alpha\). \(\alpha\) is vaguely interpreted as being the combination of a porosity factor \(\epsilon\), and a sorption distribution coefficient \(K_d\), described as “a generic term devoid of mechanism”
\begin{equation} \alpha = \epsilon + \rho\cdot K_d \end{equation}
It is claimed that for anions, \(K_d\) can be treated as negative, giving \(\alpha < \epsilon\). I have criticized this mixing of what actually are incompatible models in an earlier blog post. Strictly, this use of a “generic term devoid of mechanism” means that the evaluated \(\alpha\) should not be interpreted in any particular way. Nevertheless, the way this study is referenced in other publications, \(\alpha\) is interpreted as an effective porosity. It should be noticed, however, that this study is performed with a background electrolyte of NaClO4. The only chloride (or iodide) present is therefore at trace level, and it cannot be excluded that a mechanism of true sorption influences the results (there are indications that this is the case in other studies).
For the present assessment we anyway assume that \(\alpha\) directly quantifies the anion equilibrium between clay and the external solution (i.e. equivalent to the incorrect way of assuming that \(\alpha\) quantifies a volume accessible to chloride). It should be kept in mind, though, that effects of anion equilibrium and potential true sorption is not resolved by the single parameter \(\alpha\).
In practice, then, the model is
\begin{equation} \frac{\partial c}{\partial t} = D_p\frac{\partial^2 c}{\partial x^2} \tag{1} \end{equation}
where \(c\) is the concentration in the clay of the isotope under consideration, and the diffusion coefficient is written \(D_p\) to acknowledge that it is a pore diffusivity (when referring to models and parameter evaluations in Mo03 we will use the notation “\(D_a\)”). The boundary conditions are
\begin{equation} c(0,t) = \alpha \cdot C_0 \;\;\;\; c(L,t) = 0 \tag{2} \end{equation}
where \(C_0\) is the concentration in the source reservoir,1 and \(L\) is the sample length.
This model — that we have discussed before — has a relatively simple analytical solution, and the outflux can be written
\begin{equation} j^\mathrm{out}(t) = j^\mathrm{ss}\left (1 + 2 \sum_{n=1}^\infty \left (-1 \right )^n e^{-\frac{\pi^2n^2D_pt}{L^2}} \right) \end{equation}
where \(j^\mathrm{ss}\) is the corresponding steady-state flux. Here, the steady-state flux is related to the other parameters as
\begin{equation} j^\mathrm{ss} = \alpha\cdot D_p \frac{C_0}{L} \tag{3} \end{equation}
“Fast” and “slow” processes
Oddly, Mo03 model the system as if two independent diffusion processes are simultaneously active. They refer to these as the “fast” and the “slow” processes, and hypothesize that they relate to diffusion in interlayer water2 and “interparticle water”,3 respectively.
The “fast” process is the “ordinary” process that is assumed to reach steady state during the course of the test, and that is the focus of other through-diffusion studies. The “slow” process, on the other hand, is introduced to account for the frequent observation that measured tracer profiles are usually significantly non-linear near the interface to the source reservoir (discussed briefly above). I guess that the reason for this concentration variation is due to swelling when the sample is unloaded. But even if the reason is not fully clear, it can be directly ruled out that it is the effect of a second, independent, diffusion process — because this is not how diffusion works!
If anions move both in interlayers and “interparticle water”, they reasonably transfer back and forth between these domains, resulting in a single diffusion process (the diffusivity of such a process depends on the diffusivity of the individual domains and their geometrical configuration). To instead treat diffusion in each domain as independent means that these processes are assumed to occur without transfer between the domains, i.e. that the bentonite is supposed to contain isolated “interlayer pipes”, and “interparticle pipes”, that don’t interact. It should be obvious that this is not a reasonable assumption. Incidentally, this is how all multi-porous models assume diffusion to occur (while simultaneously assuming that the domains are in local equilibrium…).
We will thus focus on the “fast” process in this assessment, although we also use the information provided by the parameters for the “slow” process. Mo03 report the fitted values for \(D_a\) and \(\alpha\) in a table (and diagrams), and only show a comparison between model and measured data in a single case: for iodide diffusion at 0.1 M background concentration and density 1.6 g/cm3. To make any kind of assessment of the quality of these estimations we therefore have to focus on this experiment (the article states that these results are “typical high clay density data”).
Outflux
The first thing to note is that the modeled accumulated diffusive substance does not correspond to the analytical solution for the diffusion process. Here is a figure of the experimental data and the reported model (as presented in the article), that also include the solution to eqs. 1 and 2.
In fact, the model presented in Mo03 has an incorrect time dependency in the early stages. Here is a comparison between the presented model and analytical solutions in the transient stage
With the given boundary conditions, the solutions to the diffusion equation inevitably has zero slope at \(t = 0\),4 reflecting that it takes a finite amount of time for any substance to reach the outflux boundary. The models presented in Mo03, on the other hand, has a non-zero slope in this limit. I cannot understand the reason for this (is it an underlying problem with the model, or just a graphical error?), but it certainly puts all reported parameter values in doubt.
The preferred way to evaluate diffusion data is, in my opinion, to look at the flux evolution rather than the evolution of the accumulated amount of diffused substance. Converting the reported data to flux, gives the following picture.5
From a flux evolution it is easier to establish the steady-state, as it reaches a constant. It furthermore gives a better understanding for how well constrained the model is by the data. As is seen from the figure, the model is not at all very well constrained, as the experimental data almost completely miss the transient stage. (And, again, it is seen that the model in the paper with \(D_a= 9\cdot 10^{-11}\) m/s2 does not correspond to the analytical solution.)
The short transient stage is a consequence of using thin samples (0.5 cm). Compared e.g. to Muurinen et al (1988), who used three times as long samples, the breakthrough time is here expected to be \(3^2 = 9\) times shorter. As Muurinen et al. (1988) evaluated breakthrough times in the range 1 — 9 days, we here expect very short times. Here are the breakthrough times for all chloride diffusion tests, evaluated from the reported diffusion coefficients (“fast” process) using the formula \(t_\mathrm{bt} = L^2/(6D_a)\).
| Test | \(D_a\) | \(t_\mathrm{bt}\) |
| (m2/s) | (days) | |
| 0.4/0.01 | \(8\cdot 10^{-10}\) | 0.06 |
| 0.4/0.1 | \(9\cdot 10^{-10}\) | 0.05 |
| 0.4/0.1 | \(8\cdot 10^{-10}\) | 0.06 |
| 0.8/0.01 | \(3.5\cdot 10^{-10}\) | 0.14 |
| 0.8/0.1 | \(3.5\cdot 10^{-10}\) | 0.14 |
| 0.8/0.1 | \(3.7\cdot 10^{-10}\) | 0.13 |
| 1.2/0.01 | \(1.4\cdot 10^{-10}\) | 0.34 |
| 1.2/0.1 | \(2.3\cdot 10^{-10}\) | 0.21 |
| 1.2/0.1 | \(2.0\cdot 10^{-10}\) | 0.24 |
| 1.6/0.1 | \(1.0\cdot 10^{-10}\) | 0.48 |
| 1.8/0.01 | \(2\cdot 10^{-11}\) | 2.41 |
| 1.8/0.1 | \(5\cdot 10^{-11}\) | 0.96 |
| 1.8/0.1 | \(5.5\cdot 10^{-11}\) | 0.88 |
The breakthrough time is much shorter than a day in almost all tests! To sample the transient stage properly requires a sampling frequency higher than \(1/t_{bt}\). As seen from the provided example of a outflux evolution, this is not the case: The second measurement is done after about 1 day, while the breakthrough time is about 0.5 days (moreover, the first measurement appears as an outlier). We have no information on sampling frequency in the other tests, but note that to properly sample e.g. the tests at 0.8 g/cm3 requires measurements at least every third hour or so. For 0.4 g/cm3, the required sample frequency is once an hour! This design choice puts more doubt on the quality of the evaluated parameters.
Concentration profile
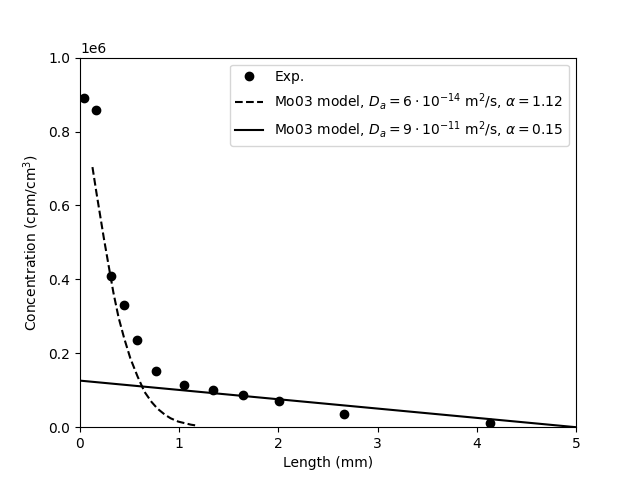
The measured concentration profile across the 1.6/0.1 iodide sample, and corresponding model results are presented in Mo03 in a figure very similar to this
Here the two models correspond to the “slow” and “fast” process discussed above (a division, remember, that don’t make sense). Zooming in on the “linear” part of the profile, we can compare the “fast” process with analytical solutions (eqs. 1 and 2)
The analytical solutions correspond directly to the outflux curves presented above. We note that the analytical solution with \(D_p = 9\cdot 10^{-11}\) m/s2 corresponds almost exactly to the model presented by Mo03. As this model basically has the same steady state flux and diffusion coefficient, we expect this similarity. It is, however, still a bit surprising, since the corresponding outflux curve of the model in Mo03 was seen to not correspond to the analytical solution. This continues to cast doubt on the model used for evaluating the parameters.
We furthermore note that the evolution of the activity of the source reservoir is not reported. Once in the text is mentioned that the “carrier concentration” is \(10^{-6}\) M, but since we don’t know how much of this concentration corresponds to the radioactive isotope, we can not directly compare with reported concentration profile across the sample (whose concentration unit is counts per minute per cm3). By extrapolating the above model curve with \(\alpha = 0.15\), we can however deduce that the corresponding source activity for this particular sample is \(C_0 = 1.26\cdot 10^5/0.15\) cpu/cm3 \(= 8.40\cdot 10^5\) cpu/cm3. But it is unsatisfying that we cannot check this independently. Also, we can of course not assume that this value of \(C_0\) is the same in any other of the tests (in particular those involving chloride). We thus lack vital information (\(C_0\)) to be able to make a full assessment of the model fitting.
It should furthermore be noticed that the experimental concentration profile does not constrain the models very well. Indeed, the adopted model (diffusivity \(9\cdot 10^{-11}\) m/s2) misses the two rightmost concentration points (which corresponds to half the sample!). A model that fits this part of the profile has a considerable higher diffusivity, and a correspondingly lower \(\alpha\) (note that the product \(D_p\cdot \alpha\) is constrained by the steady-state flux, eq. 3).
More peculiarities of the modeling is found if looking at the “slow” process (remember that this is not a real diffusion process!). Zooming in on the interface part of the profile and comparing with analytical solutions gives this picture
Here we note that an analytical solution coincides with the model presented in Mo03 with parameters \(D_a = 6\cdot 10^{-14}\) m2/s and \(\alpha = 1.12\) only if it is propagated for about 15 days! Given that no outflux measurements seem to have been performed after about 4 days (see above), I don’t now what to make of this. Was the test actually conducted for 15 days? If so, why is not more of the outflux measured/reported? (And why were the samples then designed to give a breakthrough time of only a few hours?)
Without knowledge of for how long the tests were conducted, the reported diffusion parameters becomes rather arbitrary, especially for the low density samples. For e.g. the samples of density 0.4 g/cm3, even the “slow” process has a diffusivity high enough to reach steady-state within a few days. Simulating the processes with the reported parameters gives the following profiles if evaluated after 1 and 4 days, respectively
The line denoted “total” is what should resemble the measured (unreported) data. It should be clear from these plots that the division of the profile into two separate parts is quite arbitrary. It follows that the evaluated diffusion parameters for the process of which we are interested (“fast”) has little value.
Summary and verdict
We have seen that the reported model fitting leaves a lot of unanswered questions: some of the model curves don’t correspond to the analytical solutions, information on evolution times and source concentrations is missing, and the modeled profiles are divided quite arbitrary into two separate contributions (which are not two independent diffusion process).
Moreover, the ion population (divalent vs. monovalent cations) of the samples are not known, but there are strong reasons to believe that the 0.01 M tests contain a significant amount of divalent ions, while the 0.1 M samples are partly converted to a more pure sodium state.
Also, the small size of the samples contributes to more uncertainty, both in terms of density, but also for the flux evolution because the breakthrough times becomes very short.
Based on all of these uncertainties, I mean that the results of Mo03 does not contribute to quantitative process understanding and my decision is to not to use the study for e.g. validating models of anion exclusion.
A confirmation of the uncertainty in this study is given by considering the density dependence on the chloride equilibrium concentrations for constant background concentration, evaluated from the reported diffusion parameters (\(\alpha\) for the “fast” process).
If these results should be taken at face value, we have to accept a very intricate density dependence: for 0.1 M background, the equilibrium concentration is mainly constant between densities 0.3 g/cm3 and 0.7 g/cm3, and increases between densities 1.0 g/cm3 and 1.45 g/cm3 (or, at least, does not decrease). For 0.01 M background, the equilibrium concentration instead falls quite dramatically between between densities 0.3 g/cm3 and 0.7 g/cm3, and thereafter displays only a minor density dependence.
To accept such dependencies, I require a considerably more rigorous experimental procedure and evaluation. In this case, I rather view the above plot as a confirmation of large uncertainties in parameter evaluation and sample properties.
- Chloride content: UNKNOWN
- Extracting anion equilibrium concentrations from through-diffusion tests
- Assessment of chloride equilibrium concentrations: Muurinen et al. (1988)
Footnotes
[1] Strictly, \(c(0,t)\) relates to the concentration in the endpoint of the inlet filter. But we ignore filter resistance in this assessment, which is valid for the 1.6/0.1 sample. Moreover, the filter diffusivities are not reported in Mo03.
[2] Mo03 refer to interlayer pores as “intralayer” pores, which may cause some confusion.
[3] Apparently, the authors assume an underlying stack view of the material.
[4] It may be objected that the analytical solution do not include the filter resistance. But note that filter resistance only will increase the delay. Moreover, the transport capacity of the sample in this test is so low that filters have no significant influence.
[5] The model by Mo03 looks noisy because I have read off values of accumulated concentration from the published graph. The “noise” occurs because the flux is evaluated from the concentration data by the difference formula:
\begin{equation} \bar{j}(\bar{t}_i) =\frac{1}{A} \frac{a(t_{i+1})-a(t_i)}{t_{i+1}-t_{i}} \end{equation}
where \(t_i\) and \(t_{i+1}\) are the time coordinates for two consequitive data points, \(a(t)\) is the accumulated amount diffused substance at time \(t\), \(A\) is the cross sectional area of the sample, \(\bar{t}_i = (t_{i+1} + t_i)/2\) is the average time of the considered time interval, and \(\bar{j}\) denotes the average flux during this time interval.