The vast majority of published tests on ion diffusion in bentonite deal with chemically uniform systems, and in a previous blog post I addressed the lack of studies where actual chemical gradients are maintained. But recently such a study was published: “Influence of salinity gradients on the diffusion of water and ionic species in dual porosity clay samples” (Tertre et al., 2024). Although I’m pleased to see these types of experiments being reported, I must admit that the paper as a whole leaves me quite disappointed.
The paper follows a structure recognizable from several others that we have considered previously on the blog: It starts off with an introduction section containing several incorrect or unfounded statements1 regarding bentonite.2 It then presents some experimental results that makes it evident that no real progress has been made for a long time regarding e.g. experimental design.3 The major part of the paper is devoted to a “results and discussion” section with several incorrect statements and inferences, speculation, and irrelevant modeling.
Here I would like to focus on how the study “Seeming steady-state uphill diffusion of \(^{22}\mathrm{Na}^+\) in compacted montmorillonite” (Glaus et al., 2013) is referenced:
[I]nfluence of a background electrolyte concentration gradient on the diffusion of anionic and cationic species at trace concentrations has […] been rarely investigated. Notable exceptions are the DR-A in situ diffusion experiment conducted at the Mont-Terri laboratory (Soler et al., 2019), and an “uphill” diffusion experiment of a \(^{22}\mathrm{Na}^+\) tracer in a compacted sodium montmorillonite (Glaus et al., 2013). These two studies demonstrated the marked influence of background electrolyte concentration gradient on tracer diffusion, and thus the necessity to understand the couplings between diffusion of several charged species present at contrasting concentrations and experiencing different concentration gradients. The experiment from Glaus et al. (2013) also demonstrated the importance of considering diffusion processes occurring in the porosity next to the charged surface of clay minerals (i.e., the porosity associated to the EDL of particles).
This quotation contains two statements relating to Glaus et al. (2013), both of which I think are problematic4
- It basically claims that the “uphill” phenomenon is due to diffusive couplings between several types of ions. Of course, ion diffusion always involves couplings between different types of ions, due to the requirement of electroneutrality. But it is clear that Tertre et al. (2024) mean that the “uphill” effect is caused by additional couplings that are not present in chemically homogeneous systems.
- It says that Glaus et al. (2013) demonstrates the importance to consider diffuse layers. I agree with this, but it is written in a way that implies that there also are other relevant “porosities”, and that there are other types of tests where ion diffusion in bentonite is not significantly influenced by the presence of diffuse layers.
As one of the authors of the “uphill” study, I would here like to argue for why I think the above statements are problematic and give some background context.
The “uphill” diffusion experiment
The “uphill” study actually originated from a prediction presented by me in a conference poster session. This poster discussed the role of the quantity \(D_e\), using the exact same theory that we had previously used to explain the diffusive behavior of tracer ions in compacted bentonite as an effect of Donnan equilibrium in a homogeneous system. In particular, it pointed out that \(D_e\) — although universally referred to as the (effective) “diffusion coefficient” — is not a diffusion coefficient in the context of compacted bentonite. I have continued this discussion in later papers, and in several posts on this blog.
In the poster, we suggested the “uphill” experiment as a demonstration of the shortcoming of \(D_e\). If the two reservoirs in a through-diffusion test are maintained at different background concentrations, the theory predicts a non-zero tracer flux for a vanishing external tracer concentration difference, i.e. an “infinite” value of \(D_e\). The suggestion caught the interest of an experimental group, and after a successful collaboration we could present the results of an actual “uphill” experiment. Without making too much of an exaggeration, I would say that the results of this experiment were basically exactly as predicted.
Given this background, it should be clear that the tests in Glaus et al. (2013) follow exactly the same rules as tests in chemically homogeneous systems, rather than demonstrating “the necessity to understand the couplings between diffusion of several charged species present at contrasting concentrations”. Although it is quite clearly stated already in the abstract in Glaus et al. (2013), there is apparently still a need to communicate this explanation. Let me therefore try that here.
The “uphill” diffusion phenomenon explained
Consider an ordinary aqueous solution containing radioactive \(^{22}\mathrm{Na}\) and stable \(^{23}\mathrm{Na}\). The fraction of \(^{22}\mathrm{Na}\) ions can be written \(c_\mathrm{ext}/C_\mathrm{bkg}\), where \(c_\mathrm{ext}\) is the \(^{22}\mathrm{Na}\) concentration, and \(C_\mathrm{bkg}\) is the total sodium concentration (the “tracer” and “background” concentrations, respectively).
Since \(^{23}\mathrm{Na}\) and \(^{22}\mathrm{Na}\) are basically chemically indistinguishable, the same \(^{22}\mathrm{Na}\)-fraction will be maintained in any system with which this solution is in equilibrium. In particular, if the solution is in equilibrium with a montmorillonite interlayer solution, we can write
\begin{equation*} \frac{c_\mathrm{int}}{C_\mathrm{int}} = \frac{c_\mathrm{ext}}{C_\mathrm{bkg}} \tag{1} \end{equation*}
where \(c_\mathrm{int}\) and \(C_\mathrm{int}\) are the \(^{22}\mathrm{Na}\) and total interlayer concentrations, respectively. The total interlayer cation concentration (\(C_\mathrm{int}\)) can be handled in different ways, but it is important to note that this is a substantial number under all conditions, relating to the cation exchange capacity.5 Rearranging eq. 1 gives
\begin{equation*} c_\mathrm{int} = \frac{C_\mathrm{int}}{C_\mathrm{bkg}}\cdot c_\mathrm{ext} \end{equation*}
Since the interlayer cation concentration is always larger than the corresponding background concentration, the above equation tells us that the corresponding interlayer tracer concentration becomes enhanced, by the factor \(C_\mathrm{int}/C_\mathrm{bkg}\).
Conventional through-diffusion
This enhancement mechanism causes the diffusional behavior of \(^{22}\mathrm{Na}\) in conventional through-diffusion experiments in bentonite. In such experiments, the tracer concentration in the target reservoir is usually kept near zero, and the actual steady-state concentration gradient in the interlayers is
\begin{equation*} \frac{\partial c_\mathrm{int}}{\partial x} = \frac{0- C_\mathrm{int}/C_\mathrm{bkg}\cdot c_\mathrm{ext}^{(1)}} {L} = -\frac{C_\mathrm{int}}{C_\mathrm{bkg}}\cdot \frac{ c_\mathrm{ext}^{(1)} }{ L } \end{equation*}
where we have indexed the tracer concentration in the source reservoir with “\((1)\)”, labeled the sample length \(L\), and assumed that ions diffuse in the \(x\)-direction. The corresponding flux is thus (Fick’s law)
\begin{equation*} j_\mathrm{steady-state} = – \phi D_c\frac{\partial c_\mathrm{int}}{\partial x} = \phi D_c\cdot \frac{C_\mathrm{int}}{C_\mathrm{bkg}}\cdot \frac{c_\mathrm{ext}^{(1)} } {L} \tag{2} \end{equation*}
where \(D_c\) denotes the (macroscopic) diffusivity in the interlayers, and \(\phi\) is porosity. Keeping \(c_\mathrm{ext}^{(1)}\) constant, eq. 2 shows that the \(^{22}\mathrm{Na}\) steady-state flux increases indefinitely as the background concentration is made small, in full agreement with experimental observation.6
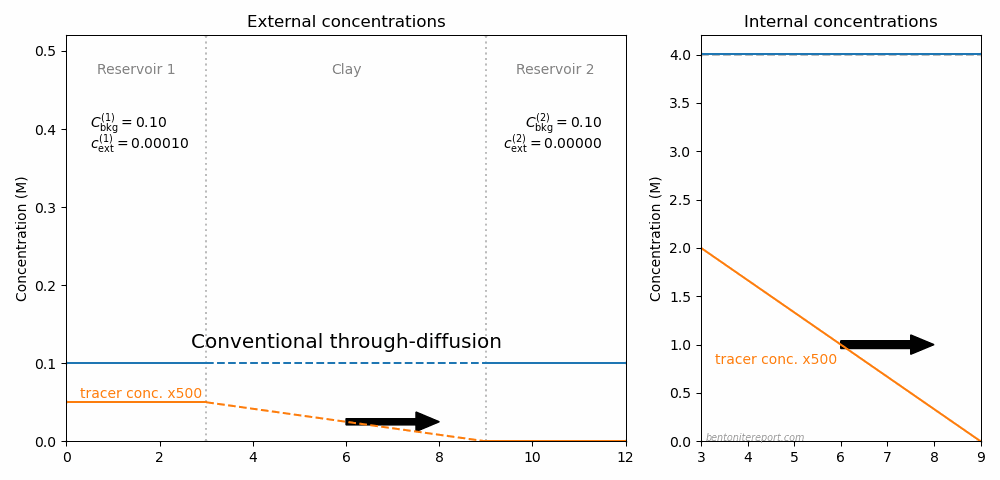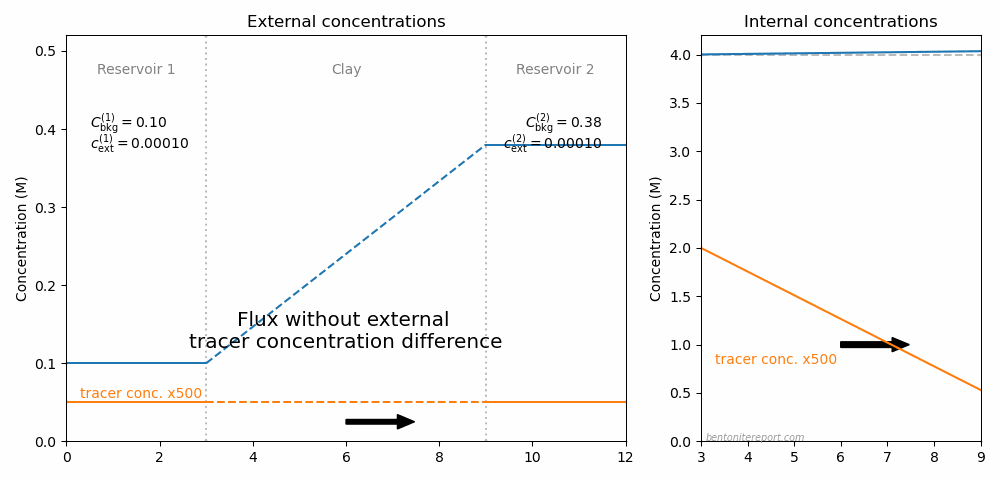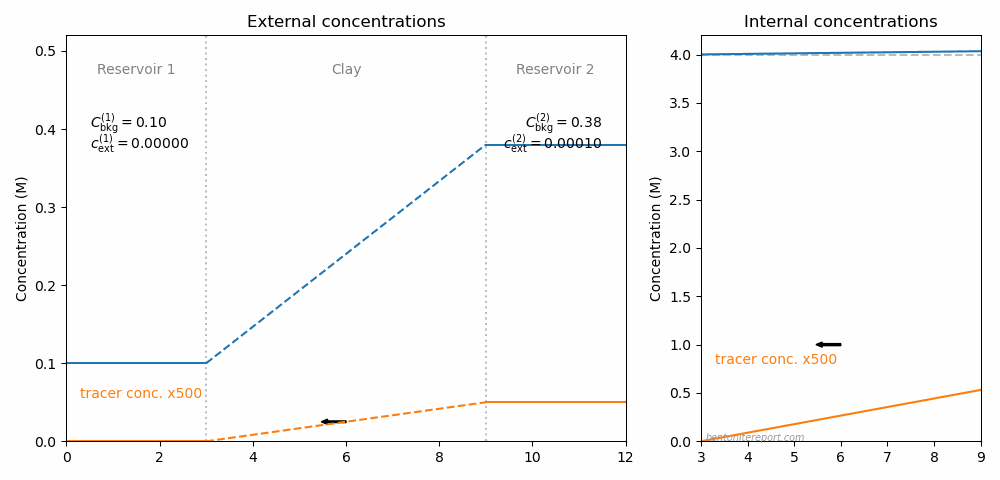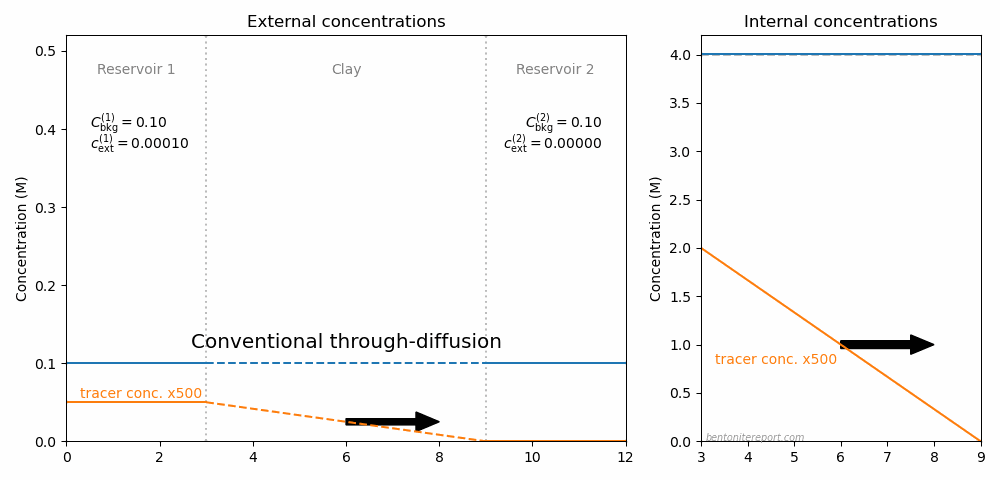
The picture below illustrates the concentration conditions in an conventional through-diffusion test.
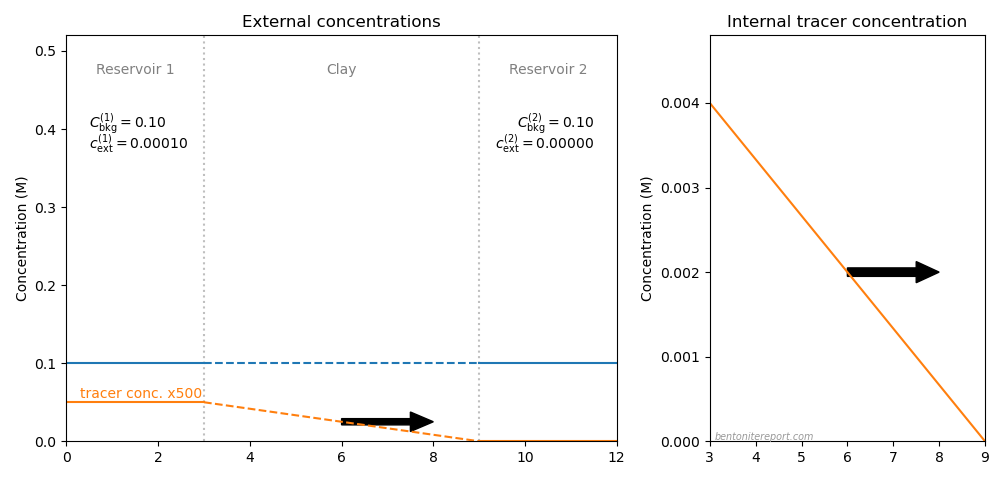
Here we have chosen \(C_\mathrm{int}=\) 4.0 M, the background concentration in the two reservoirs (blue) is put equal to 0.1 M, and the tracer concentration (orange) is put to 0.1 mM in reservoir 1 (and zero i reservoir 2). The corresponding internal tracer gradient is plotted in the right side diagram, and the resulting diffusive flux is indicated by the arrow.
“Uphill” diffusion
To explain the “uphill” effect the only modifications needed in the above derivation is to allow for different background concentrations in the external reservoirs, and to recognize that the tracer concentration in the clay on the “target” side (indexed “\((2)\)”) no longer is zero. Considering the tracer concentration enhancement at both interfaces, the steady-state interlayer concentration gradient then reads
\begin{equation*} \frac{\partial c_\mathrm{int}}{\partial x} = \frac{ C_\mathrm{int}/C_\mathrm{bkg}^{(2)}\cdot c_\mathrm{ext}^{(2)} -C_\mathrm{int}/C_\mathrm{bkg}^{(1)}\cdot c_\mathrm{ext}^{(1)}} {L} \end{equation*}
To be more concrete, let’s assume that \(C_\mathrm{bkg}^{(2)} = 5\cdot C_\mathrm{bkg}^{(1)}\), which is the same ratio as in Glaus et al. (2013). We then have
\begin{equation*} \frac{\partial c_\mathrm{int}}{\partial x} = \frac{C_\mathrm{int}}{C_\mathrm{bkg}^{(1)}} \cdot \frac{ c_\mathrm{ext}^{(2)}/5 – c_\mathrm{ext}^{(1)}} {L} \end{equation*}
giving the corresponding steady-state flux
\begin{equation*} j_\mathrm{steady-state} = \phi D_c\cdot \frac{C_\mathrm{int}}{C_\mathrm{bkg}^{(1)}} \cdot \frac{ c_\mathrm{ext}^{(1)} – c_\mathrm{ext}^{(2)}/5} {L} \end{equation*}
Note that we recover the conventional through-diffusion result (eq. 2) from this expression, if we put \(c_\mathrm{ext}^{(2)}= 0\). But if we e.g. set the tracer concentration equal in both reservoirs, we still have a flux from side \((1)\) to side \((2)\), of size \(j = 4/5 \cdot \phi D_c\cdot C_\mathrm{int}/C_\mathrm{bkg}^{(1)}\cdot c_\mathrm{ext}^{(1)}\). And even if we make \(c_\mathrm{ext}^{(2)}\) larger than \(c_\mathrm{ext}^{(1)}\) — as long as \(c_\mathrm{ext}^{(1)}< c_\mathrm{ext}^{(2)} < 5\cdot c_\mathrm{ext}^{(1)}\) — we still have a diffusive flux from side \((1)\) to side \((2)\), i.e seeming “uphill” diffusion.
Below is illustrated the concentration conditions in an “uphill” configuration.
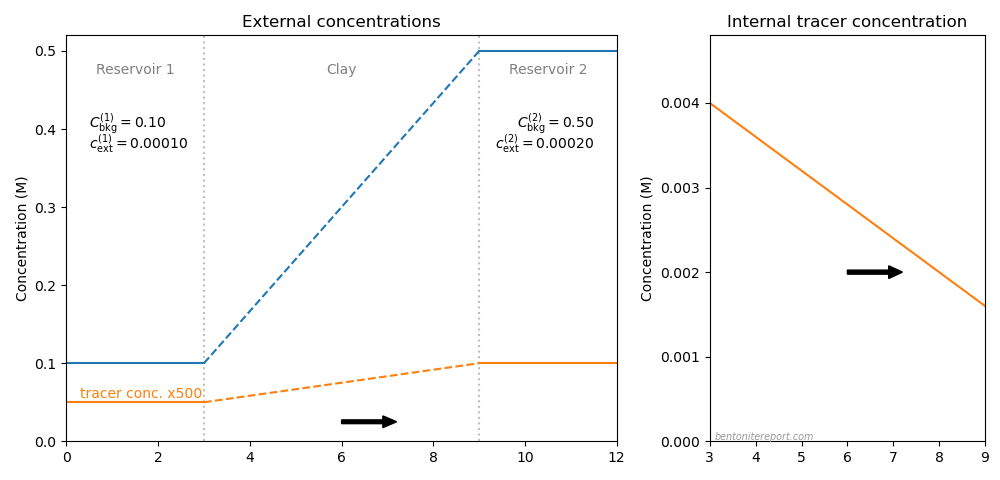
In contrast to the above illustration for conventional through-diffusion, the background concentration in reservoir 2 is here raised to 0.5 M and the tracer concentration in reservoir 2 is put equal to 0.2 mM. We see that, although tracers are transported to the reservoir with higher concentration, the process is still ordinary Fickian diffusion, as the internal tracer gradient has the same direction as in the conventional case.
We can now conclude what was stated above: The “uphill” diffusion effect is caused by exactly the same mechanism that cause the behavior of cation diffusion in conventional bentonite through-diffusion tests. This mechanism is ion equilibrium between clay and external solutions at the two interfaces. In this particular case, with sodium tracers diffusing in a sodium background, we don’t need to invoke the full ion equilibrium framework in order to quantify the fluxes, but can rely on the very robust result that any two systems in equilibrium have the same tracer fraction (eq. 1).
Reexamining the Tertre et al. (2024) statements
With the explanation for the “uphill” effect established, let’s re-examine the problematic statements in Tertre et al. (2024) identified above
- Glaus et al. (2013) cannot be used to support a claim of “marked influence” of additional diffusional couplings. The opposite is true: Glaus et al. (2013) found no significant influence from mechanisms beyond those in chemically homogeneous conditions.
- The “uphill” effect was predicted from taking the idea seriously that diffusion in compacted bentonite is fully governed by interlayer properties. Singling out Glaus et al. (2013) as the study that demonstrates the importance of diffuse layers7 therefore gives the wrong impression. Rather, what Glaus et al. (2013) demonstrates, in conjunction with corresponding conventional through-diffusion results, is that compacted bentonite contains insignificant amounts of bulk water (what Tertre et al. (2024) call “interparticle water”).
A way forward (if anybody cares)
After the uphill study was published I was for a while under the illusion that things would begin to change within the compacted bentonite research field. Not only did the study, to my mind, deal a fatal blow to any bentonite model that relies on the presence of a bulk water phase in the clay. It also opened up a whole new area of interesting studies to conduct. Now, some 11 years later, I can disappointingly conclude that not a single additional study has been presented that explore the ideas here discussed.8 And, regarding bentonite models, bulk water is apparently alive and kicking, as has been discussed ad nauseum on this blog.
Experimentally, there are a number of interesting questions looking for answers. In particular, we actually do expect additional mechanisms to play a role in chemically inhomogeneous systems, e.g. osmosis, and other effects due to presence of salt concentration gradients and electrostatic potential differences. It may be argued for why such effects are not significant in Glaus et al. (2013), but it is of course both of fundamental and practical interest to understand under which conditions they are. The original “uphill” study is e.g. performed at quite extreme density (\(1900\;\mathrm{m^3/kg}\)). How would the result differ at \(1600\;\mathrm{m^3/kg}\) or \(1300\;\mathrm{m^3/kg}\)? Also, how would the results change with other choices of the reservoir concentrations, and how would the results differ if one of the cations is not at trace level (e.g. a system with comparable amounts of sodium and potassium)?
Even under the conditions of the original study, there are several predictions left to verify. If e.g. \(c^{(1)}_\mathrm{ext} = c^{(2)}_\mathrm{ext}/5\), the theory predicts zero flux (implying \(D_e = 0\)). The theory also implies that when performing “conventional” through-diffusion, the actual level of the background concentration in the target reservoir is irrelevant, as long as the tracer concentration is kept at zero.
In fact, one can imagine making a whole cycle of through-diffusion tests to explore the ideas here discussed, as illustrated in this animation
The resulting steady-state flux for various external conditions is indicated by the arrow. Here, the full ion equilibrium framework was used to calculate the internal concentrations (giving an internal gradient also in \(C_\mathrm{int}\)). Background concentrations and total interlayer concentration is chosen to be comparable with Glaus et al. (2013), while the choice for tracer concentration is arbitrary.9
With the risk of sounding hubristic, the number of experiments suggested in the above animation could have given enough material for several Ph.D. theses. But here we are, in the year 2024, without even a replication of the “uphill” effect. Instead, a basically entire research field has been stuck for decades with the ludicrous idea that models of compacted bentonite should be based on a bulk water description. I find this both hilarious and horrific.
Footnotes
[1] For example (follow links to discussions on these issues):
- It states the traditional diffusion-sorption model as being relevant in these systems. It is not.
- It somehow manages to combine the traditional diffusion-sorption model with the effective porosity model for anion tracer diffusion, although these two models are incompatible.
- Related to using the traditional diffusion-sorption model, it assumes \(D_e\) to be a real diffusion coefficient, which it is not. I find this particularly remarkable in a paper that deals with the presence of “saline gradients”. A motivation behind e.g. the “uphill” test is to point out the shortcomings of \(D_e\), as discussed in the rest of this blog post.
- It claims that “anionic and cationic tracers do not experience the same overall accessible porosity”, which is unjustified.
- It claims that “diffusion rates” of anions are decreased and “diffusion rates” of cations are increased, compared to “neutral species”, due to different interactions with diffuse layers. But this is not true generally.
- It implicitly simply assumes a “stack”-view of these clay systems. But stacks don’t make much sense.
[2] I use the word “bentonite” here quite loosely. Tertre et al. (2024) use wordings such as “clayey samples”, “argillaceous rocks” and “clayey formation”, but it is clear that the presented material is supposed to apply to actual bentonite.
[3] I’m specifically thinking about that cation tracer through-diffusion tests at low background concentration is not a good idea, and that it is completely clear from the results presented in Tertre et al. (2024) that some of these are mainly controlled by diffusion in the confining filters. Estimating a “rock capacity factor” larger than 750 for sodium tracers in a sodium-clay (at 20 mM background concentration) should have set off all alarm bells.
[4] Regarding Soler et al. (2019), I think that whole study is problematic, which I might argue for in a separate blog post.
[5] Glaus et al. (2013) invoke the “exchange site” activity \([\mathrm{NaX}]\) to discuss this quantity. I personally prefer relating it to the quantity \(c_\mathrm{IL}\) that is defined within the homogeneous mixture model.
[6] This agreement has been shown to be quantitative, see e.g. Glaus et al. (2007), Birgersson and Karnland (2009) and Birgersson (2017). Note that this result is quite independent on how many “porosities” you choose to include in a model; it’s merely a consequence of treating the dominating pores (interlayers) adequately. Further, note that measuring the diverging fluxes in the limit of low background concentration becomes increasingly difficult, as the confining filters becomes rate limiting.
[7] In the present context, I presume the terms “diffuse layer” and “interlayer” to be more or less equivalent. Other authors instead make an unjustified distinction, that I have addressed here.
[8] There are a few examples of published studies where effects of the kind discussed here are present, but where the authors don’t seem to be aware of it.
[9] Tracer concentrations in Glaus et al. (2013) is much smaller, but this value does not affect any behavior, as long as it is small in comparison with total concentration.
