To celebrate that I have built myself a tool for solving the Poisson-Boltzmann equation for two parallel charged plates and specified external solution, here is a cosy little animation
The animation shows the anion concentration profile (blue) between the plates as the distance varies, in systems in equilibrium with an external 100 mM 1:1 salt solution. Also plotted is the corresponding internal concentration level as calculated from the ideal Donnan equilibrium formula (orange). The layer charge density in the Poisson-Boltzmann calculation is 0.111 C/m2, and the corresponding cation exchange capacity in the Donnan calculation is 0.891 eq/kg.
As the distance between the plates increases, the Poisson-Boltzmann profile increasingly deviates from the Donnan concentration. At lower density (larger plate distance) it is clear that the Poisson-Boltzmann solution allows for considerably more anions between the plates as compared with the Donnan result. On the other hand, for denser systems, the difference between the two solutions decreases; this is especially true when considering the relative difference — keep in mind that the external concentration is kept constant, at 100 mM.
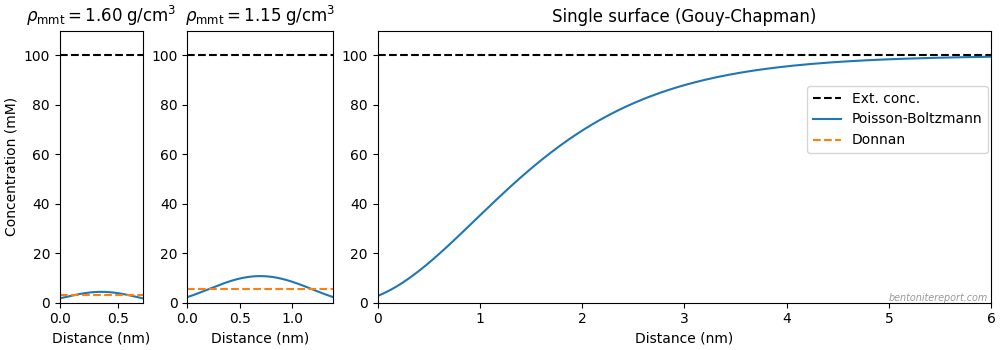
In fact, in systems relevant for e.g. radioactive waste storage — spanning an effective montmorillonite density range from \(\rho_\mathrm{mmt} =\) 1.60 g/cm3 to \(\rho_\mathrm{mmt} =\) 1.15 g/cm3, say — the difference between the Poisson-Boltzmann and the Donnan results is virtually negligible (it should also be kept in mind that the continuum assumption underlying the Poisson-Boltzmann calculation is not valid in this density range). Here are plotted snapshots of these two limiting cases, together with the Poisson-Boltzmann solution for a single plate (the Gouy-Chapman model)
This figure clearly shows that the Gouy-Chapman model is not at all valid in any relevant system, unless you postulate larger voids in the bentonite. But why would you do that?