Monthly Archives: November 2021

The failure of Archie’s law validates the homogeneous mixture model

Leave a reply

A testable difference

In the homogeneous mixture model, the effective diffusion coefficient for an ion in bentonite is evaluated as

\begin{equation} D_e = \phi \cdot \Xi \cdot D_c \tag{1} \end{equation}

where \(\phi\) is the porosity of the sample, \(D_c\) is the macroscopic pore diffusivity of the presumed interlayer domain, and \(\Xi\) is the ion equilibrium coefficient. \(\Xi\) quantifies the ratio between internal and external concentrations of the ion under consideration, when the two compartments are in equilibrium.

In the effective porosity model, \(D_e\) is instead defined as

\begin{equation} D_e = \epsilon_\mathrm{eff}\cdot D_p \tag{2} \end{equation}

where \(\epsilon_\mathrm{eff}\) is the porosity of a presumed bulk water domain where anions are assumed to reside exclusively, and \(D_p\) is the corresponding pore diffusivity of this bulk water domain.

We have discussed earlier how the homogeneous mixture and the effective porosity models can be equally well fitted to a specific set of anion through-diffusion data. The parameter “translation” is simply \(\phi\cdot \Xi \leftrightarrow \epsilon_\mathrm{eff}\) and \(D_c \leftrightarrow D_p\). It may appear from this equivalency that diffusion data alone cannot be used to discriminate between the two models.

But note that the interpretation of how \(D_e\) varies with background concentration is very different in the two models.

  • In the homogeneous mixture model, \(D_c\) is not expected to vary with background concentration to any greater extent, because the diffusing domain remains essentially the same. \(D_e\) varies in this model primarily because \(\Xi\) varies with background concentration, as a consequence of an altered Donnan potential.
  • In the effective porosity model, \(D_p\) is expected to vary, because the volume of the bulk water domain, and hence the entire domain configuration (the “microstructure”), is postulated to vary with background concentration. \(D_e\) thus varies in this model both
    because \(D_p\) and \(\epsilon_\mathrm{eff}\) varies.

A simple way of taking into account a varying domain configuration (as in the effective porosity model) is to assume that \(D_p\) is proportional to \(\epsilon_\mathrm{eff}\) raised to some power \(n – 1\), where \(n > 1\). Eq. 2 can then be written

\begin{equation} D_e = \epsilon_\mathrm{eff}^n\cdot D_0 \tag{3} \end{equation} \begin{equation}\text{ (effective porosity model)} \end{equation}

where \(D_0\) is the tracer diffusivity in pure bulk water. Eq. 3 is in the bentonite literature often referred to as “Archie’s law”, in analogy with a similar evaluation in more conventional porous systems. Note that with \(D_0\) appearing in eq. 3, this expression has the correct asymptotic behavior: in the limit of unit porosity, the effective diffusivity reduces to that of a pure bulk water domain.

Eq. 3 shows that \(D_e\) in the effective porosity model is expected to depend non-linearly on background concentration for constant sample density. In contrast, since \(D_c\) is not expected to vary significantly with background concentration, we expect a linear dependence of \(D_e\) in the homogeneous mixture model. Keeping in mind the parameter “translation” \(\phi\cdot\Xi \leftrightarrow \epsilon_\mathrm{eff}\), the prediction of the homogeneous mixture model (eq. 1) can be expressed1

\begin{equation} D_e = \epsilon_\mathrm{eff}\cdot D_c \tag{4} \end{equation} \begin{equation} \text{ (homogeneous mixture model)} \end{equation}

We have thus managed to establish a testable difference between the effective porosity and the homogeneous mixture model (eqs. 3 and 4). This is is great! Making this comparison gives us a chance to increase our process understanding.

Comparison with experiment

Van Loon et al. (2007)

It turns out that the chloride diffusion measurements performed by Van Loon et al. (2007) are accurate enough to resolve whether \(D_e\) depends on “\(\epsilon_\mathrm{eff}\)” according to eqs. 3 or 4. As will be seen below, this data shows that \(D_e\) varies in accordance with the homogeneous mixture model (eq. 4). But, since Van Loon et al. (2007) themselves conclude that \(D_e\) obeys Archie’s law, and hence complies with the effective porosity model, it may be appropriate to begin with some background information.

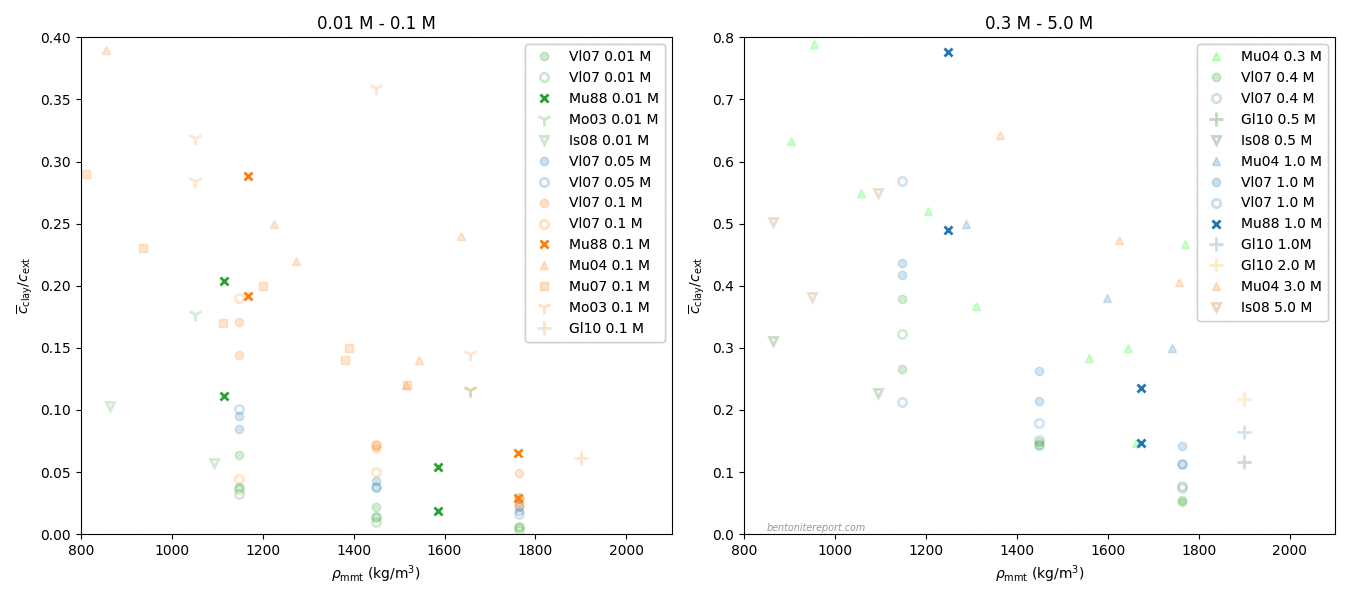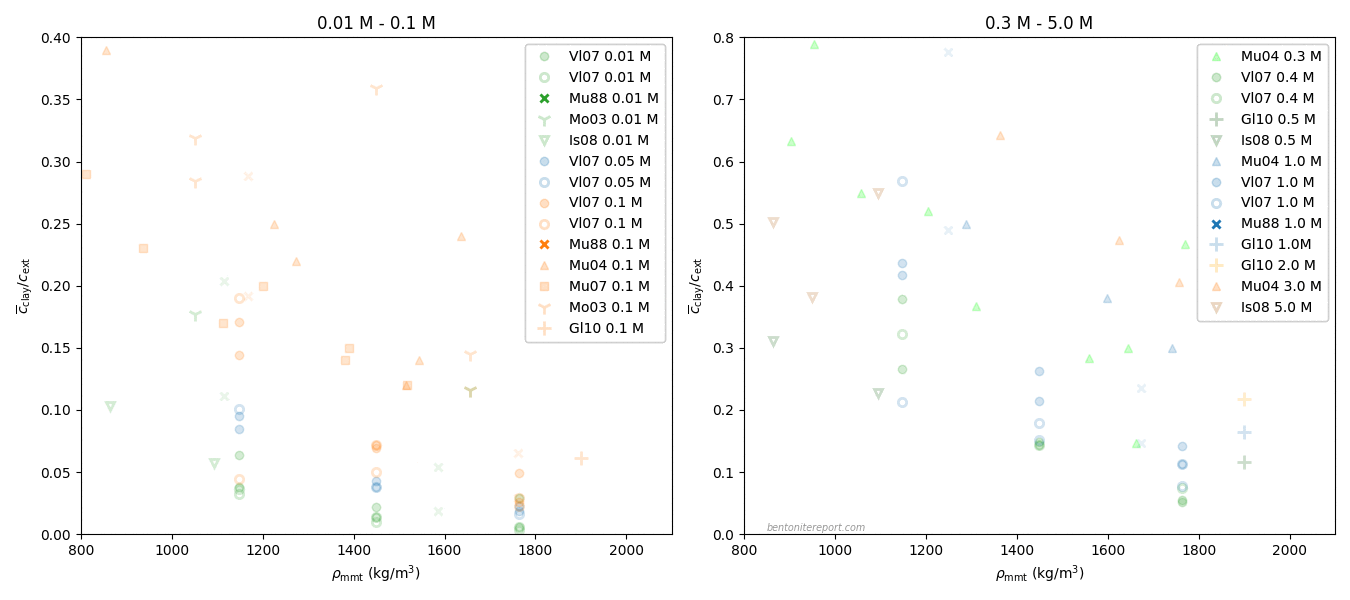
Van Loon et al. (2007) report three different series of diffusion tests, performed on bentonite samples of density 1300, 1600, and 1900 kg/m3, respectively. For each density, tests were performed at five different NaCl background concentrations: 0.01 M, 0.05 M, 0.1 M, 0.4 M, and 1.0 M. The tests were evaluated by fitting the effective porosity model, giving the effective diffusion coefficient \(D_e\) and corresponding “effective porosity” \(\epsilon_\mathrm{eff}\) (it is worth repeating that the latter parameter equally well can be interpreted in terms of an ion equilibrium coefficient).

Van Loon et al. (2007) conclude that their data complies with eq. 3, with \(n = 1.9\), and provide a figure very similar to this one

Effective diffusivity vs. "effective porsity" for a bunch of studies (fig 8 in Van Loon et al. (2007))

Here are compared evaluated values of effective diffusivity and “effective porosity” in various tests. The test series conducted by Van Loon et al. (2007) themselves are labeled with the corresponding sample density, and the literature data is from García-Gutiérrez et al. (2006)2 (“Garcia 2006”) and the PhD thesis of A. Muurinen (“Muurinen 1994”). Also plotted is Archie’s law with \(n\) =1.9. The resemblance between data and model may seem convincing, but let’s take a further look.

Rather than lumping together a whole bunch of data sets, let’s focus on the three test series from Van Loon et al. (2007) themselves, as these have been conducted with constant density, while only varying background concentration. This data is thus ideal for the comparison we are interested in (we’ll get back to commenting on the other studies).

It may also be noted that the published plot contains more data points (for these specific test series) than are reported in the rest of the article. Let’s therefore instead plot only the tabulated data.3 The result looks like this

Effective diffusivity vs. "effective porosity" as evaluated in Van Loon et al. (2007) compared with Archie's law (n=1.9) and the homogenous mixter model predictions.

Here we have also added the predictions from the homogeneous mixture model (eq. 4), where \(D_c\) has been fitted to each series of constant density.

The impression of this plot is quite different from the previous one: it should be clear that the data of Van Loon et al. (2007) agrees fairly well with the homogeneous mixture model, rather than obeying Archie’s law. Consequently, in contrast to what is stated in it, this study refutes the effective porosity model.

The way the data is plotted in the article is reminiscent of Simpson’s paradox: mixing different types of dependencies of \(D_e\) gives the illusion of a model dependence that really isn’t there. Reasonably, this incorrect inference is reinforced by using a log-log diagram (I have warned about log-log plots earlier). With linear axes, the plots give the following impression

Effective diffusivity vs. "effective porosity" as evaluated in Van Loon et al. (2007) compared with Archie's law (n=1.9) and the homogenous mixter model predictions. Linear diagram axes.

This and the previous figure show that \(D_e\) depends approximately linearly on “\(\epsilon_\mathrm{eff}\)”, with a slope dependent on sample density. With this insight, we may go back and comment on the other data points in the original diagram.

García-Gutiérrez et al. (2006) and Muurinen et al. (1988)

The tests by García-Gutiérrez et al. (2006) don’t vary the background concentration (it is not fully clear what the background concentration even is4), and each data point corresponds to a different density. This data therefore does not provide a test for discriminating between the models here discussed.

I have had no access to Muurinen (1994), but by examining the data, it is clear that it originates from Muurinen et al. (1988), which was assessed in detail in a previous blog post. This study provides two estimations of “\(\epsilon_\mathrm{eff}\)”, based on either breakthrough time or on the actual measurement of the final state concentration profile. In the above figure is plotted the average of these two estimations.5

One of the test series in Muurinen et al. (1988) considers variation of density while keeping background concentration fixed, and does not provide a test for the models here discussed. The data for the other two test series is re-plotted here, with linear axis scales, and with both estimations for “\(\epsilon_\mathrm{eff}\)”, rather than the average6

Effective diffusivity vs. "effective porosity" as evaluated in Muurinen et al. (1988) compared with Archie's law (n=1.9) and the homogenous mixter model predictions. Linear diagram axes.

As discussed in the assessment of this study, I judge this data to be too uncertain to provide any qualitative support for hypothesis testing. I think this plot confirms this judgment.

Glaus et al. (2010)

The measurements by Van Loon et al. (2007) are enough to convince me that the dependence of \(D_e\) for chloride on background concentration is further evidence for that a homogeneous view of compacted bentonite is principally correct. However, after the publication of this study, the same authors (partly) published more data on chloride equilibrium, in pure Na-montmorillonite and “Na-illite”,7 in Glaus et al. (2010).

This data certainly shows a non-linear relation between \(D_e\) and “\(\epsilon_\mathrm{eff}\)” for Na-montmorillonite, and Glaus et al. (2010) continue with an interpretation using “Archie’s law”. Here I write “Archie’s law” with quotation marks, because they managed to fit the expression to data only by also varying the prefactor. The expression called “Archie’s law” in Glaus et al. (2010) is

\begin{equation} D_e = A\cdot\epsilon_\mathrm{eff}^n \tag{5} \end{equation}

where \(A\) is now a fitting parameter. With \(A\) deviating from \(D_0\), this expression no longer has the correct asymptotic behavior as expected when interpreting \(\epsilon_\mathrm{eff}\) as quantifying a bulk water domain (see eq. 3). Nevertheless, Glaus et al. (2010) fit this expression to their measurements, and the results look like this (with linear axes)

Effective diffusivity vs. "effective porosity" as evaluated in Glaus al. (2010) compared with "Archie's law" (n=1.9, fitted A) and the homogenous mixter model predictions. Linear diagram axes.

Here is also plotted the prediction of the homogeneous mixture model (eq. 4). For the montmorillonite data, the dependence is clearly non-linear, while for the “Na-illite” I would say that the jury is still out.

Although the data for montmorillonite in Glaus et al. (2010) is non-linear, there are several strong arguments for why this is not an indication that the effective porosity model is correct:

  • Remember that this result is not a confirmation of the measurements in Van Loon et al. (2007). As demonstrated above, those measurements complies with the homogeneous mixture model. But even if accepting the conclusion made in that publication (that Archie’s law is valid), the Glaus et al. (2010) results do not obey Archie’s law (but “Archie’s law”).
  • The four data points correspond to background concentrations of 0.1 M, 0.5 M, 1.0 M, and 2.0 M. If “\(\epsilon_\mathrm{eff}\)” represented the volume of a bulk water phase, it is expected that this value should level off, e.g. as the Debye screening length becomes small (Van Loon et al. (2007) argue for this). Here “\(\epsilon_\mathrm{eff}\)” is seen to grow significantly, also in the transition between 1.0 M and 2.0 M background concentration.
  • These are Na-montmorillonite samples of dry density 1.9 g/cm3. With an “effective porosity” of 0.067 (the 2.0 M value), we have to accept more than 20% “free water” in these very dense systems! This is not even accepted by other proponents of bulk water in compacted bentonite.

Furthermore, these tests were performed with a background of \(\mathrm{NaClO_4}\), in contrast to Van Loon et al. (2007), who used chloride also for the background. The only chloride around is thus at trace level, and I put my bet on that the observed non-linearity stems from sorption of chloride on some system component.

Insight from closed-cell tests

Note that the issue whether or not \(D_e\) varies linearly with “\(\epsilon_\mathrm{eff}\)” at constant sample density is equivalent to whether or not \(D_p\) (or \(D_c\)) depends on background concentration. This is similar to how presumed concentration dependencies of the pore diffusivity for simple cations (“apparent” diffusivities) have been used to argue for multi-porosity in compacted bentonite. For cations, a closer look shows that no such dependency is found in the literature. For anions, it is a bit frustrating that the literature data is not accurate or relevant enough to fully settle this issue (the data of Van Loon et al. (2007) is, in my opinion, the best available).

However, to discard the conceptual view underlying the effective porosity model, we can simply use results from closed-cell diffusion studies. In Na-montmorillonite equilibrated with deionized water, Kozaki et al. (1998) measured a chloride diffusivity of \(1.8\cdot 10^{-11}\) m2/s at dry density 1.8 g/cm3.8 If the effective porosity hypothesis was true, we’d expect a minimal value for the diffusion coefficient9 in this system, since \(\epsilon_\mathrm{eff}\) approaches zero in the limit of vanishing ionic strength. Instead, this value is comparable to what we can evaluate from e.g. Glaus et al. (2010) at 1.9 cm3/g, and 2.0 M background electrolyte: \(D_e/\epsilon_\mathrm{eff} = 7.2\cdot 10^{-13}/0.067\) m2/s = \(1.1\cdot 10^{-11}\) m2/s.

That chloride diffuses just fine in dense montmorillonite equilibrated with pure water is really the only argument needed to debunk the effective porosity hypothesis.

Footnotes

[1] Note that \(\epsilon_\mathrm{eff}\) is not a parameter in the homogeneous mixture model, so eq. 4 looks a bit odd. But it expresses \(D_e\) if \(\phi\cdot \Xi\) is interpreted as an effective porosity.

[2] This paper appears to not have a digital object identifier, nor have I been able to find it in any online database. The reference is, however, Journal of Iberian Geology 32 (2006) 37 — 53.

[3] This choice is not critical for the conclusions made in this blog post, but it seems appropriate to only include the data points that are fully described and reported in the article.

[4] García-Gutiérrez et al. (2004) (which is the study compiled in García-Gutiérrez et al. (2006)) state that the samples were saturated with deionized water, and that the electric conductivity in the external solution were in the range 1 — 3 mS/cm.

[5] The data point labeled with a “?” seems to have been obtained by making this average on the numbers 0.5 and 0.08, rather than the correctly reported values 0.05 and 0.08 (for the test at nominal density 1.8 g/cm3 and background concentration 1.0 M).

[6] Admittedly, also the data we have plotted from the original tests in Van Loon et al. (2007) represents averages of several estimations of “\(\epsilon_\mathrm{eff}\)”. We will get back to the quality of this data in a future blog post when assessing this study in detail, but it is quite clear that the estimation based on the direct measurement of stable chloride is the more robust (it is independent of transport aspects). Using these values for “\(\epsilon_\mathrm{eff}\)”, the corresponding plot looks like this

Effective diffusivity vs. "effective porosity" as evaluated in Van Loon et al. (2007) compared with Archie's law (n=1.9) and the homogenous mixter model predictions. Linear diagram axes. The data for "effective porosity" evaluated solely from measurements of stable chloride measurements.

Update (220721): Van Loon et al. (2007) is assessed in detail here.

[7] To my mind, it is a misnomer to describe something as illite in sodium form. Although “illite” seems to be a bit vaguely defined, it is clear that it is supposed to only contain potassium as counter-ion (and that these ions are non-exchangeable; the basal spacing is \(\sim\)10 Å independent of water conditions). The material used in Glaus et al. (2010) (and several other studies) has a stated cation exchange capacity of 0.22 eq/kg, which in a sense is comparable to the montmorillonite material (a factor 1/4). Shouldn’t it be more appropriate to call this material e.g. “mixed-layer”?

[8] This value is the average from two tests performed at 25 °C. The data from this study is better compiled in Kozaki et al. (2001).

[9] Here we refer of course to the empirically defined diffusion coefficient, which I have named \(D_\mathrm{macr.}\) in earlier posts. This quantity is model independent, but it is clear that it should be be associated with the pore diffusivities in the two models here discussed (i.e. with \(D_c\) in the homogeneous mixture model, and with \(D_p\) in the effective porosity model).

Assessment of chloride equilibrium concentrations: Muurinen et al. (1988)

Leave a reply

In the ongoing assessment of chloride equilibrium concentrations in bentonite, we here take a closer look at the study by Muurinen et al. (1988), in the following referred to as Mu88.1 In the quite messy plot containing all reported chloride equilibrium concentrations, we thus investigate the twelve points indicated here

Mu88 points highlighted in plot with all chloride equilibrium data

Mu88 performed both chloride and uranium through-diffusion tests on “MX-80” bentonite, as well as sorption tests. Here we focus solely on the chloride diffusion. We also disregard one diffusion test series that does not vary external concentration (it was conducted with an unspecified “artificial groundwater” and varied sample density).

Left are two test series performed with nominal sample densities 1.2 g/cm3 and 1.8 g/cm3, respectively. For each of these densities, chloride through-diffusion tests were performed with external NaCl concentrations of 0.01 M, 0.1 M, and 1.0 M, respectively. The samples were cylindrical with a diameter of 3.0 cm, and a length of 1.5 cm, giving a volume of 10.6 cm3. To refer to a specific test or sample, we use the nomenclature “nominal density/external concentration”, e.g. the test performed at nominal density 1.2 g/cm3 and external solution 0.1 M is referred to as “1.2/0.1”.

Uncertainty of bentonite samples

“MX-80” is not the name of some specific standardized material, but simply a product name.2 It is quite peculiar that that “MX-80” nevertheless is a de facto standard in the research field for clay buffers in radwaste repositories. But, being a de facto standard, several batches of bentonite with this name have been investigated and reported throughout the years. We consequently have some appreciation for its constitution, and the associated variation.

In Mu88, the material used is only mentioned by name, and it is only mentioned once (in the abstract!). We therefore can’t tell which of the studies that is more appropriate to refer to. Instead, let’s take a look at how “MX-80” has been reported generally.

ReportBatch yearMmt contentCECNa-content
(%)(eq/kg)(%)
TR-06-30 (“WySt”)198082.50.7683
NTR 83-12< 198375.50.7686
TR-06-30 (“WyL1”)199579.50.77–
TR-06-30 (“WyL2”)199979.80.7571
TR-06-30 (“WyR1”)200182.70.7575
TR-06-30 (“WyR2”)200180.00.7171
NTB 01-08< 2002–0.79*85
WR 2004-023< 200480 — 850.84*65
*) These values were derived from summing the exchangeable ions, and are probably overestimations.

Montmorillonite content

Reported montmorillonite content varies in the range 75 — 85%. For the present context, this primarily gives an uncertainty in adopted effective montmorillonite dry density, which, in turn, is important for making relevant comparison between bentonite materials with different montmorillonite content. For the “MX-80” used in Mu88 we here assume a montmorillonite content of 80%. In the table below is listed the corresponding effective montmorillonite densities when varying the montmorillonite content in the range \(x =\) 0.75 — 0.85, for the two nominal dry densities.

Dry densityEMDD (\(x\)=0.75)EMDD (\(x\)=0.80)EMDD (\(x\)=0.85)
(g/cm3)(g/cm3)(g/cm3)(g/cm3)
1.21.011.051.09
1.81.611.661.70

The uncertainty in montmorillonite content thus translates to an uncertainty in effective montmorillonite dry density on the order of 0.1 g/cm3.

Cation population

While reported values of the cation exchange capacity of “MX-80” are relatively constant, of around 0.75 eq/kg,4 the reported fraction of sodium ions is seen to vary, in the range 70 — 85 %. The remaining population is mainly di-valent rare-earth metal ions (calcium and magnesium). This does not only mean that different studies on “MX-80” may give results for quite different types of systems, as the mono- to di-valent ion ratio may vary, but also that samples within the study may represent quite different systems. We examine this uncertainty below, when discussing the external solutions.

Soluble calcium minerals

The uncertainty of how much divalent cations are available is in fact larger than just discussed. “MX-80” is reported to contain a certain amount of soluble calcium minerals, in particular gypsum. These provide additional sources for divalent ions, which certainly will be involved in the chemical equilibration as the samples are water saturated. Reported values of gypsum content in “MX-80” are on the order of 1%. With a molar mass of 0.172 kg/mol, this contributes to the calcium content by \(2\cdot 0.01/0.172\) eq/kg \(\approx 0.12\) eq/kg, or about 16% of the cation exchange capacity.

Sample density

The samples in Mu88 that we focus on have nominal dry density of 1.2 and 1.8 g/cm3. The paper also reports measured porosities on each individual sample, listed in the below table together with corresponding values of dry density5

Test\(\phi\)\(\rho_d\)
(-)(g/cm3)
1.2/0.010.541.27
1.2/0.10.521.32
1.2/1.00.491.40
1.8/0.010.371.73
1.8/0.10.311.89
1.8/1.00.341.81

We note a substantial variation in measured density for samples with the same nominal density: for the 1.2 g/cm3 samples, the standard deviation is 0.06 g/cm3, and for the 1.8 g/cm3 samples it is 0.07 g/cm3. Moreover, while the mean value for the 1.8 g/cm3 samples is close to the nominal value (1.81 g/cm3), that for the 1.2 g/cm3 samples is substantially higher (1.33 g/cm3).

It is impossible to know from the information provided in Mu88 if this uncertainty is intrinsic to the procedure of preparing the samples, or if it is more related to the procedure of measuring the density at test termination.6

Uncertainty of external solutions

Mu88 do not describe how the external solutions were prepared. We assume here, however, that preparing pure NaCl solutions gives no significant uncertainty.

Further, the paper contains no information on how the samples were water saturated, nor on the external solution volumes. Since samples with an appreciable amount of di-valent cations are contacted with pure sodium solutions, it is unavoidable that an ion exchange process is initiated. As we don’t know any detail of the preparation process, this introduces an uncertainty of the exact aqueous chemistry during the course of a test.

To illustrate this problem, here are the results from calculating the exchange equilibrium between a sample initially containing 30% exchangeable charge in form of calcium (70% sodium), and external NaCl solutions of various concentrations and volumes

calcium remaining in the bentonite as a function of inital external NaCl concentration for various volumes

In these calculations we assume a sample of density 1.8 g/cm3 with the same volume as in Mu88 (10.6 cm3), a cation exchange capacity of 0.75 eq/kg, and a Ca/Na selectivity coefficient of 5.

In a main series, we varied the external volume between 50 and 1000 ml (solid lines). While the solution volume naturally has a significant influence on the process, it is seen that the initial calcium content essentially remain for the lowest concentration (0.01 M). In contrast, for a 1.0 M solution, a significant amount of calcium is exchanged for all the solution volumes.

The figure also shows a case for sample density 1.2 g/cm3 (dashed line), and a scenario where equilibrium has been obtained twice, with a replacement of the first solution (to a once again pure NaCl solution) (dot-dashed line).

The main lesson from these simulations is that the actual amount of di-valent ions present during a diffusion test depends on many details: the way samples were saturated, volume of external solutions, if and how often solutions were replaced, time, etc. It is therefore impossible to state the exact ion population in any of the tests in Mu88. But, guided by the simulations, it seems very probable that the tests performed at 0.01 M contain a substantial amount of di-valent ions, while those performed at 1.0 M probably resemble more pure sodium systems.

The only information on external solutions in Mu88 is that the “solution on the low concentration side was changed regularly” during the course of a test. This implies that the amount of di-valent cations may not even be constant during the tests.

Uncertainty of diffusion parameters

The diffusion parameters explicitly listed in Mu88 are \(D_e\) and “\(D_a\)”, while it is implicitly understood that they have been obtained by fitting the effective porosity model to outflux data and the measured clay concentration profile in the final state. “\(D_a\)” is thus really the pore diffusivity \(D_p\),7 and relates to \(D_e\) as \(D_e = \epsilon_\mathrm{eff} D_p\), where \(\epsilon_\mathrm{eff}\) is the so-called “effective porosity”. In a previous blog post, we discussed in detail how anion equilibrium concentrations can be extracted from through-diffusion tests, and the results derived there is used extensively in this section.

Rather than fitting the model to the full set of data (i.e. outflux evolution and final state concentration profile), diffusion parameters in Mu88 have been extracted in various limits.

Evaluation of \(D_e\) in Mu88

The effective diffusivity was obtained by estimating the steady-state flux, dividing by external concentration difference of the tracer, and multiplying by sample length \begin{equation} D_e = \frac{j^\mathrm{ss}\cdot L}{c^\mathrm{source}}\tag{1} \end{equation}

Here it is assumed that the target reservoir tracer concentration can be neglected (we assume this throughout). Eq. 1 is basically eq. 1 in Mu88 (and eq. 8 in the earlier blog post), from which we can evaluate the values of the steady-state flux that was used for the reported values of \(D_e\) (\(A \approx 7.1\) cm2 denotes sample cross sectional area)

Test\(D_e\)\(A\cdot j^\mathrm{ss}/c^\mathrm{source}\)
(\(\mathrm{m^2/s}\))(ml/day)
1.2/0.01\(7.7\cdot 10^{-12}\)0.031
1.2/0.1\(2.9\cdot 10^{-11}\)0.118
1.2/1.0\(1.2\cdot 10^{-10}\)0.489
1.8/0.01\(3.3\cdot 10^{-13}\)0.001
1.8/0.1\(4.8\cdot 10^{-13}\)0.002
1.8/1.0\(4.0\cdot 10^{-12}\)0.016

The figure below compares the evaluated values of the steady-state flux with the flux evaluated from the measured target concentration evolution,8 for samples with nominal dry density 1.8 g/cm3 (no concentration data was reported for the 1.2 g/cm3 samples)

outflux vs. time for 1.8 g/cm3 samples in Muurinen et al. (1988)

These plots clearly show that the transition to steady-state is only resolved properly for the test with highest background concentration (1.0 M). It follows that the uncertainty of the evaluated steady-state — and, consequently, of the evaluated \(D_e\) values — increases dramatically with decreasing background concentration for these samples.

Evaluation of \(D_p\) in Mu88

Pore diffusivities were obtained in two different ways. One method was to relate the steady-state flux to the clay concentration profile at the end of the test, giving \begin{equation} D_{p,c} = \frac{j^\mathrm{ss}\cdot L}{\phi\cdot\bar{c}(0)} \tag{2} \end{equation}

where \(\bar{c}(0)\) denotes the chloride clay concentration at the interface to the source reservoir. The quantity in eq. 2 is called “\(D_{ac}\)”7 in Mu88, and this equation is essentially the same as eq. 2 in Mu889 (and eq. 10 in the previous blog post). Using the steady-state fluxes, we can back-calculate the values of \(\bar{c}(0)\) used for this evaluation of \(D_{p,c}\)

Test\(D_{p,c}\)\(A\cdot j^\mathrm{ss}/c^\mathrm{source}\)\(\phi\)\(\bar{c}(0)/c^\mathrm{source}\)
(\(\mathrm{m^2/s}\))(ml/day)(-)(-)
1.2/0.01\(7.0\cdot 10^{-11}\)0.0310.540.204
1.2/0.1\(2.8\cdot 10^{-10}\)0.1180.520.199
1.2/1.0\(5.1\cdot 10^{-10}\)0.4890.490.480
1.8/0.01\(2.0\cdot 10^{-11}\)0.0010.370.045
1.8/0.1\(3.1\cdot 10^{-11}\)0.0020.310.050
1.8/1.0\(5.2\cdot 10^{-11}\)0.0160.340.226

Note that, although we did some calculations to obtain them, the values for \(\bar{c}(0)/c^\mathrm{source}\) in this table are closer to the actual measured raw data (concentrations). We made the calculation above to “de-derive” these values from the reported diffusion coefficients (combining eqs. 1 and 2 shows that \(\bar{c}(0)\) is obtained from the reported parameters as \(\bar{c}(0)/c^\mathrm{source} = D_e/(\phi D_{p,c})\)).

Here are compared the measured concentration profiles for the samples of nominal density 1.8 g/cm3 and the corresponding slopes used to evaluate \(D_{p,c}\) (profiles for the 1.2 g/cm3 samples are not provided in Mu88)

Final state concentration profiles for 1.8 g/cm3 samples in Muurinen et al. (1988)

For background concentrations 1.0 M and 0.1 M, the evaluated slope corresponds quite well to the raw data. For the 0.01 M sample, however, the match not very satisfactory. I suspect that a detection limit may have been reached for the analysis of the profile of this sample. Needless to say, the evaluated value of \(\bar{c}(0)\) is very uncertain for the 0.01 M sample.

It may also be noted that all measured concentration profiles deviates from linearity near the interface to the source reservoir. This is a general behavior in through-diffusion tests, which I am quite convinced of is related to sample swelling during dismantling, but there are also other suggested explanations. Here we neglect this effect and relate diffusion quantities to the linear parts of profiles, but this issue should certainly be treated in a separate discussion.

\(D_p\) was also evaluated in a different way in Mu88, by measuring what we here will call the breakthrough time, \(t_\mathrm{bt}\) (Mu88 call it “time-lag”). This quantity is fairly abstract, and relates to the asymptotic behavior of the analytical expression for the outflux that apply for constant boundary concentrations (we here assume them to be \(c^\mathrm{source}\) and 0, respectively). This expression is displayed in eq. 7 in the previous blog post.

Multiplying the outflux by the sample cross sectional area \(A\) and integrating, gives the accumulated amount of diffused tracers. In the limit of long times, this quantity is, not surprisingly, linear in \(t\) \begin{equation} A\cdot j^\mathrm{ss} \cdot \left(t – \frac{L^2}{6\cdot D_p} \right ) \end{equation}

\(t_\mathrm{bt}\) is defined as the time for which this asymptotic expression is zero. Determining \(t_\mathrm{bt}\) from the measured outflux evolution consequently allows for an estimation of \(D_p\) as \begin{equation} D_{p,t} = \frac{L^2}{6t_\mathrm{bt}} \tag{3} \end{equation}

This quantity is called “\(D_{at}\)” in Mu887 (eq. 3 is eq. 3 in Mu88). With another back calculation we can extract the values of \(t_\mathrm{bt}\) determined from the raw data

Test\(D_{p,t}\)\(t_\mathrm{bt}\)
(\(\mathrm{m^2/s}\))(days)
1.2/0.01\(1.4\cdot 10^{-10}\)3.1
1.2/0.1\(2.0\cdot 10^{-10}\)2.2
1.2/1.0\(3.2\cdot 10^{-10}\)1.4
1.8/0.01\(5.0\cdot 10^{-11}\)8.7
1.8/0.1\(5.4\cdot 10^{-11}\)8.0
1.8/1.0\(7.7\cdot 10^{-11}\)5.6

These evaluated breakthrough times are indicated in the flux plots above for samples of nominal dry density 1.8 g/cm3. For the 0.1 M and 0.01 M samples it is obvious that this value is very uncertain — without a certain steady-state flux it is impossible to achieve a certain breakthrough time. The breakthrough time for the 1.8/1.0 test, on the other hand, simply appears to be incorrectly evaluated: in terms of outflux vs. time, the breakthrough time should be the time where the flux has reached 62% of the steady-state value.10

As no raw data is reported for the 1.2 g/cm3 tests, the quality of the evaluated breakthrough times cannot be checked for them. It may be noted, however, that the evaluated breakthrough times are significantly shorter in this case as compared with the 1.8 g/cm3 tests. Consequently, while the sampling frequency is high enough to properly resolve the transient stage of the outflux evolution for the 1.8g/cm3 tests, it must be substantially higher in order to resolve this stage in the 1.2g/cm3 tests (I guess a rule of thumb is that sampling frequency must be at least higher than \(1/t_{bt}\)).

With the pore diffusivities evaluated from \(t_\mathrm{bt}\) we get a second estimation of \(\bar{c}(0)/c^\mathrm{source}\), using eq. 2. These values are listed in the table below and compared with the direct evaluation from the steady-state concentration profiles.

Test\(\bar{c}(0)/c^\mathrm{source}\)\(\bar{c}(0)/c^\mathrm{source}\)
(breakthrough)(profile)
1.2/0.010.1020.204
1.2/0.10.2790.199
1.2/1.00.7650.480
1.8/0.010.0180.045
1.8/0.10.0290.050
1.8/1.00.1530.226

In a well conducted study these estimates should be similar; \(D_{p,c}\) and \(D_{p,t}\) are, after all, estimations of the same quantity: the pore diffusivity \(D_p\).7 But here we note a discrepancy of approximately a factor 2 between several values of \(\bar{c}(0)\).

It is difficult to judge generally which of the estimations are more accurate, but we have seen that for the 1.8/0.1 and 1.8/0.01 tests, the flux data is not very well resolved, giving a corresponding uncertainty on the equilibrium concentration estimated from the breakthrough time. On the other hand, also the concentration profile is poorly resolved in the case of 0.01 M at 1.8 g/cm3.

However, in cases where the value of \(\bar{c}(0)/c^\mathrm{source}\) is substantial (as for the 1.8/1.0 test and, reasonably, for all tests at 1.2 g/cm3), we expect the estimation directly from the concentration profile to be accurate and robust (as for the 1.8 g/cm3 test at high NaCl concentration). For the 1.2 g/cm3 samples we cannot say much more than this, since Mu88 don’t provide the concentration raw data. For the 1.8/1.0 test, however, we can continue the analysis by fitting the model to all available data.

Re-evaluation by fitting to the full data set

Note that all evaluations in Mu88 are based on making an initial estimation of the steady-state flux, giving \(D_e\) (eq. 1). This value of \(D_e\) (or \(j^{ss}\)) is thereafter fixed in the subsequent estimation of \(D_{p,c}\) (eq. 2). Likewise, an estimation of the steady-state flux is required for estimating the breakthrough time. Here is an animation showing the variation of the model when transitioning from the value of the pore diffusivity estimated from breakthrough time (\(7.7\cdot 10^{-11}\) m2/s), to the value estimated from concentration profile (\(5.2\cdot 10^{-11}\) m2/s) for the 1.8/1.0 test, keeping the steady-state flux fixed at the initial estimation

Note that the axes for the flux is on top (time) and to the right (accumulation rate). This animation confirms that the diffusivity evaluated from breakthrough time in Mu88 gives a way too fast process: the slope of the steady-state concentration profile is too small, and the outflux evolution has a too short transient stage. On the other hand, using the diffusivity estimated from the concentration profiles still doesn’t give a flux that fit very well. The problem is that this fitting is performed with a fixed value of the steady-state flux. By instead keeping the slope fixed at the experimental values, while varying diffusivity (and thus steady state flux), we get the following variation

This animation shows that the model can be fitted well to all data (at least for the 1.8/1.0 test). The problem with the evaluation in Mu88 is that it assumes the steady-state to be fully reached at the later stages of the test. As the above fitting procedure shows, this is only barely true. The experiments could thus have been designed better by conducting them longer, in order to better sample the steady-state phase (and the steady-state flux should have been fitted to the entire data set). Nevertheless, for this sample, the steady-state flux obtained by allowing for this parameter to vary is only slightly different from that used in Mu88 (17.5 rather than 16.3 \(\mathrm{\mu}\)l/day, corresponding to a change of \(D_p\) from \(5.2\cdot10^{-11}\) to \(5.6\cdot10^{-11}\) m2/s). Moreover, this consideration should not be a problem for the 1.2 g/cm3 tests, if they were conducted for as long time as the 1.8 g/cm3 tests, because steady-state is reached much faster (in those tests, sampling frequency may instead be a problem, as discussed above).

As we were able to fit the full model to all data, we conclude that the value of \(\bar{c}(0)/c^\mathrm{source}\) obtained from \(D_{p,c}\) is probably the more robust estimation11, and that there appears to be a problem with how the breakthrough times have been determined. For the 1.8 g/cm3 samples we have demonstrated that this is the case, for the 1.2 g/cm3 we can only make an educated guess that this is the case.

Summary and verdict

We have seen that the results on chloride diffusion in Mu88 suffer from uncertainty from several sources:

  • The “MX-80” material is not that well defined
  • Densities vary substantially for samples at the same nominal density
  • Without knowledge of e.g water saturation procedures and solution volumes, it is impossible to estimate the proper ion population during the course of a test
  • It is, however, highly likely that tests performed at low NaCl concentrations contain substantial amounts of di-valent ions, while those at high NaCl concentration are closer to being pure sodium systems.
  • The reported diffusivities give a corresponding uncertainty in the chloride equilibrium concentrations of about a factor of 2. While some tests essentially have a too high noise level to give certain estimations, the problem for the others seems to stem from the estimation of breakthrough times.

Here is an attempt to encapsulate the above information in an updated plot for the chloride equilibrium data in Mu88

Uncertainty estimations for chloride equilibrum concnetrations in Muurinen et al. (1988)

The colored squares represent “confidence areas” based on the variation within each nominal density (horizontally), and on the variation of \(\bar{c}(0)/c^\mathrm{source}\) from the two reported values on pore diffusivity7 (vertically). The limits of these rectangles are simply the 95% confidence interval, based on these variations, and assuming a normal distribution.

Data points put within parentheses are estimations judged to be improper (based on either re-evaluation of the raw data, or informed guesses).

From the present analysis my decision is to not use the data from Mu88 to e.g. validate models for anion exclusion. Although there seems to be nothing fundamentally wrong with how these test were conducted, they suffer from so many uncertainties of various sources that I judge the data to not contribute to quantitative process understanding.

Footnotes

[1] This work is referred to as “Muurinen et al. (1989)” by several authors.

[2] MX-80 is not only a brand name, but also a band name.

[3] This report is “Bentonite Mineralogy” by L. Carlson (Posiva WR 2004-02), but it appears to not be included in the INIS database. It can, however, be found with some elementary web searching.

[4] It’s interesting to note that the cation exchange capacity of “MX-80” remains more or less constant, while the montmorillonite content has some variation. This implies that the montmorillonite layer charge varies (and is negatively correlated with montmorillonite content). Could it be that the manufacturer has a specified cation exchange capacity as requirement for this product?

[5] To convert porosity to dry density, I used \(\rho_d = \rho_s\cdot(1-\phi)\), with solid grain density \(\rho_s = 2.75\) g/cm3.

[6] A speculation is that the uncertainty stems from the measurement procedure, as this was done on smaller sections of the full samples. It is not specified in Mu88 what the reported porosity represent, but it is reasonable to assume that it is the average of all sections of a sample.

[7] At the risk of losing some clarity, I refuse to use the term “apparent diffusivity” for something which actually is a real pore diffusivity.

[8] These values were not tabulated, but I have read them off from the graphs in Mu88.

[9] Mu88 use the concentration based on the total volume in their expression, while \(\bar{c}\) is defined in terms of water volume (water mass, strictly). Eq.2 therefore contains the physical porosity. In their concentration profile plots, however, Mu88 use \(\bar{c}\) as variable (called \(c_{pw}\) — the “concentration in the pore water”)

[10] Plugging the breakthrough time \(L^2/6D_p\) into the expression for the flux gives

\begin{equation} j^\mathrm{out}(t_\mathrm{bt}) = j^{ss}\cdot\left ( 1 + 2 \sum (-1)^n e^\frac{-\pi^2 n^2}{6} \right ) \approx 0.616725\cdot j^{ss} \end{equation}

I find it amusing that this value is close to the reciprocal golden ratio (0.618033…). Finding the breakthrough time from a flux vs. time plot thus corresponds (approximately) to splitting the y-axis according to the golden ratio.

[11] Note that the actual evaluated values of $D_{p,c}$ in Mu88 still may be uncertain, because they also depend on the values of the steady-state flux, which we have seen were not optimally evaluated.