Repulsion between surfaces and anions is not really the point

Many publications dealing with “anion” exclusion in compacted bentonite describe the phenomenon as being primarily due to electrostatic repulsion of anions from the negatively charged clay surfaces. This explanation, which may seem plausible both at a first and a second glance, is actually not that satisfactory. There are two major issues to consider:

• Although it is popular to use the word “anion” when referring to the phenomenon, it must be remembered that the anions are accompanied by cations, in order to maintain overall charge neutrality; it really is salt that is excluded from the bentonite. This observation shows that the above “explanation” is incomplete: it can be argued with the same logic that salt should accumulate, because the clay surfaces attract the cations of the external salt.
• Salt exclusion occurs generally in Donnan systems, also in those that lack surfaces. Its principal explanation can consequently not involve the presence of surfaces. For a simpler system, e.g. potassium ferrocyanide, the “explanation” above translates to claiming that exclusion is caused by “anions” being electrostatically repelled by the ferrocyanide ions. In this case it may be easier to spot the shortcoming of such a claim, and to consider also the potassium ions (which attract anions), as well as the role played by the cations of the excluded salt.

What, then, is the primary cause for salt exclusion? Let us continue with using potassium ferrocyanide as an example of a simple Donnan system, and then translate our findings to the case of compacted bentonite.

Ferrocyanide

Consider a potassium ferrocyanide solution separated from a potassium chloride solution by a membrane permeable to all but the ferrocyanide ions. The ionic configuration near the membrane then looks something like this

Because potassium ions can pass the membrane, and because they have an entropic driving force to migrate out of the ferrocyanide solution, a (microscopic) region is formed in the external solution next to the membrane, with an excess amount of positive charge. Similarly, a region is formed next to the membrane in the ferrocyanide solution with an excess amount of negative charge. Thus, a region of charge separation exists across the membrane — similar to the depletion zone in a p-n junction — over which the electrostatic potential varies. The electric field (= a varying potential) at the interface acts as to pull back potassium ions towards the ferrocyanide solution. The equilibrium width of the space charge region is set when the diffusive flux is balanced by the flux due to the electric field.

With a qualitative understanding of the electrostatic potential configuration we can now give the most plain answer to what causes “anion” exclusion: it is because of the potential difference across the membrane. Chloride ions behave in the opposite way as compared to potassium, with an entropic driving force to enter the ferrocyanide solution, while being pulled back towards the external solution due to the electric field across the membrane.

Here the mindful reader may perhaps object and point out that the electric field restricting the chloride inflow reasonably originates from the ferrocyanide anions. It thus may seem that “anion” exclusion, after all, is caused by repulsion from other negative charges.

Indeed, electrostatic repulsion of anions requires the “push” of some other negatively charged entity. But note that the potential is constant in the interior of the ferrocyanide solution, and only varies near the membrane. The variation of the potential is caused by separation of charge: chloride is as much “pushed” out of the ferrocyanide solution by the ferrocyanide as it is “pulled” out of it, due to electrostatic attraction, by the excess potassium on the other side. Repulsion between charges of equal sign occurs also in the interior of the ferrocyanide solution (or in any ionic solution), but does not in itself lead to salt exclusion.

Bentonite

The above description can be directly transferred to the case of compacted bentonite. Replacing the potassium ferrocyanide with e.g. K-montmorillonite, salt exclusion occurs mainly because potassium can migrate out of the clay region, while montmorillonite particles cannot. Again, we have charge separation with a resulting varying electrostatic potential across the interface.

Admittedly, the general situation is more complicated in bentonite because of the extension of montmorillonite particles; viewed as “anions”, these are irregularly shaped macromolecules with hundreds or thousands of charge centers.

The ion configuration in a bentonite suspension therefore looks quite different from a corresponding ordinary solution, as the montmorillonite charge obviously is constrained to individual particles. Dilute systems thus have charge separation on the particle scale and show salt exclusion even without charge separation at the interface to the external solution. These types of systems (suspensions) have historically been the subject of most studies on “anion” exclusion, and are usually treated theoretically using the Gouy-Chapman model.

With increasing density, however, the effect of a varying potential between montmorillonite particles diminishes, while the effect of charge separation at the interface increases. For dense systems (> 1.2 g/cm³, say), we may therefore approximate the internal potential as constant and only consider the variation across the interface to the external solution using Donnan’s “classical” framework.¹

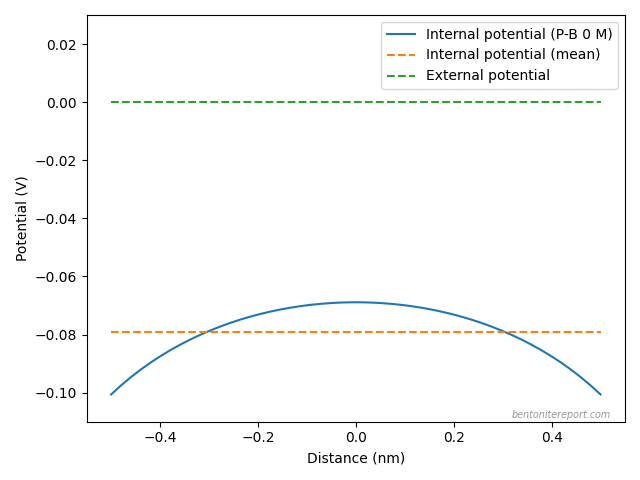
Here is an illustration of the validity of this approximation:

The figure shows the difference between the external (green) and the average internal (orange) potentials in a 1:1 system of density 1.3 g/cm³ and with external concentration 0.1 M, calculated using Donnan’s “classical” equation. Also plotted is the electrostatic potential across the interlayer (blue) as calculated using the Poisson-Boltzmann equation,² in a similar system (interlayer distance 1 nm). It is clear that the variation of the Poisson-Boltzmann potential from the average is small in comparison with the Donnan potential.

Repulsion between chloride and montmorillonite particles of course occurs everywhere in compacted bentonite, whereas the phenomenon mainly responsible for salt exclusion occurs only near the interfaces. Merely stating electrostatic repulsion as the cause for salt exclusion in compacted bentonite does not suffice, just as in the case of ferrocyanide.

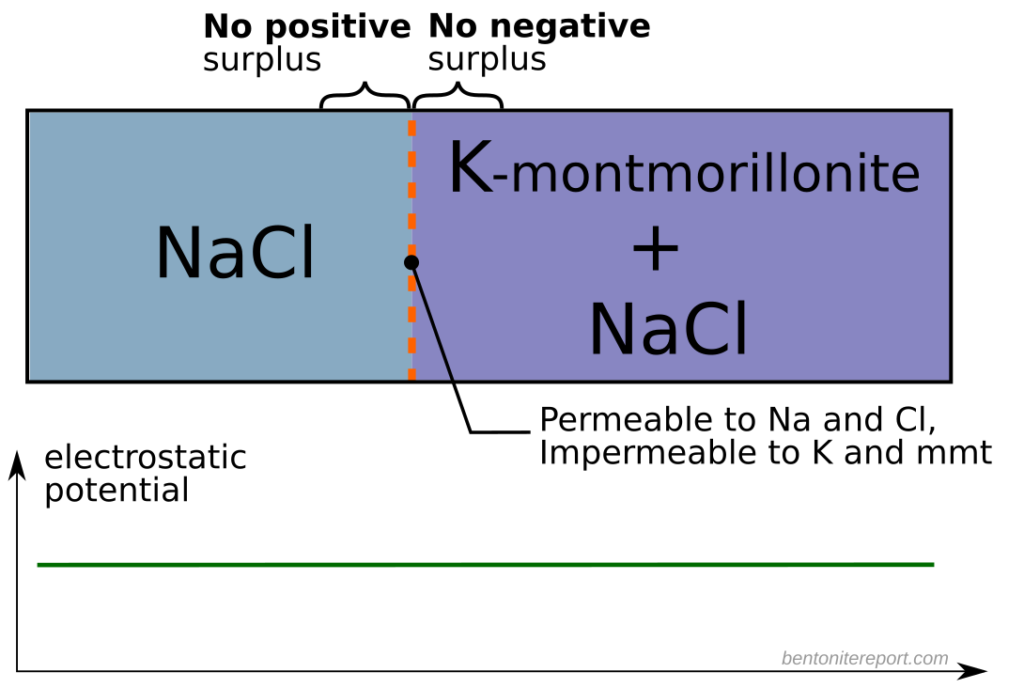
To illustrate that the salt exclusion effect depends critically on exchangeable cations being able to diffuse out of the bentonite, consider the following thought experiment.³ Compacted K-montmorillonite is contacted with a NaCl solution. But rather than having a conventional component separating the solution and the clay, we imagine a membrane that does not allow for the passage of neither potassium nor clay, but that allows for the passage of sodium and chloride. Since potassium is not allowed to diffuse out of the bentonite, no charge separation occurs across the membrane. With no space charge region, the electrostatic potential does not vary and NaCl is not excluded! (to the extent that the Donnan approximation is valid)

A charge neutral perspective

The explanation for “anion” exclusion that we have explored rests on the formation of a potential difference across the interface region between bentonite and external solution. But remember that it is salt — in our example KCl — that is excluded from the bentonite (or the ferrocyanide solution), and that the cation (K) gains energy by being transferred from the external to the internal solution. The electrical work for transferring a unit of KCl is thus zero (which makes sense since KCl is a charge neutral entity). In this light, it may seem unsatisfactory to offer the potential difference as the sole explanation for salt exclusion.

I therefore think that the following kinematic way of reasoning is very helpful. Instead of considering the mass transfer of Cl across the membrane in terms of oppositely directed “electric” and “diffusive” parts, we lump them together with equal amounts of K transfer, giving two equal but oppositely directed fluxes of KCl. Reasonably, the KCl flux into the ferrocyanide solution is proportional to the external ion concentrations

\begin{equation} j^\mathrm{in}_\mathrm{KCl} = A\cdot c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} \end{equation}

while the outflux is proportional to the internal ion concentrations

\begin{equation} j^\mathrm{out}_\mathrm{KCl} = -A\cdot c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

\(A\) is a coefficient accounting for the transfer resistance across the interface region. Requiring the sum of these fluxes to be zero gives the following relation

\begin{equation} c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} = c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

which is the (ideal) Donnan equation.

We can therefore interpret KCl exclusion as an effect of potassium in the clay providing a potential for “out-transfer”, as soon as the chance is given, i.e. when chloride enters from the external solution. From this perspective salt exclusion could maybe be said to be a form of cation “rejection”.

Footnotes

[1] Note also that the Gouy-Chapman model is not valid in the high density limit, although it is applied (or alluded to) in this limit in many publications. But e.g. Schofield (1947) states (about the Gouy-Chapman solution):

[T]he equation is applicable to cases in which the distance between opposing surfaces considerably exceeds the distance between neighboring point charges on the surfaces; for there will then be a range of electrolyte concentrations over which the radius of the ionic atmosphere is less than the former and greater than the latter.

This criterion is not met in compacted bentonite, where instead the interlayer distance is comparable to the distance between neighboring charge centers on the surfaces. Invalid application of the Gouy-Chapman model also seems to underlie the flawed but widespread “anion-accessible porosity” concept.

[2] This calculation uses the equations presented in Engström and Wennerström (1978), and assumes no excess ions and a surface charge density of 0.111 \(\mathrm{C/m^2}\). For real consistency this calculation should really be performed with the boundary condition of 0.1 M external concentration. However, since the purpose of the graph is just to demonstrate the sizes of the two potential variations, and since I have yet to acquire a reasonable tool for performing Poisson-Boltzmann calculations with non-zero external concentration, I disregard this inconsistency. Moreover, the continuum assumption of the Poisson-Boltzmann description is anyway beginning to lose its validity at these interlayer distances. Update (220831): Solutions to the Poisson-Boltzmann equation with non-zero external concentration are presented here.

[3] Perhaps this could be done as a Molecular Dynamics simulation?