Monthly Archives: October 2021

Kahr et al. (1985) — the diffusion study that could have changed everything

Leave a reply

On the surface, “Ionendiffusion in Hochverdichtetem Bentonit”1 by G. Kahr, R. Hasenpatt, and M. Müller-Vonmoos, published by NAGRA in March 1985, looks like an ordinary mundane 37-page technical report. But it contains experimental results that could have completely changed the history of model development for compacted clay.

Test principles

The tests were conducted in a quite original manner. By compacting granules or powder, the investigators obtained samples that schematically look like this

Schematics of samples in Kahr et al. (1985(

The bentonite material — which was either Na-dominated “MX-80”, or Ca-dominated “Montigel” — was conditioned to a specific water-to-solid mass ratio \(w\). At one of the faces, the bentonite was mixed with a salt (in solid form) to form a thin source for diffusing ions. This is essentially the full test set-up! Diffusion begins as soon as the samples are prepared, and a test was terminated after some prescribed amount of time, depending on diffusing ion and water content. At termination, the samples were sectioned and analyzed. In this way, the investigators obtained final state ion distributions, which in turn were related to the initial states by a model, giving the diffusion coefficients of interest.

Note that the experiments were conducted without exposing samples to a liquid (external) solution; the samples were “unsaturated” to various degree, and the diffusing ions dissolve within the bentonite. The samples were not even confined in a test cell, but “free-standing”, and consequently not under pressure. They were, however, stored in closed vessels during the course of the tests, to avoid changes in water content.

With this test principle a huge set of diffusion tests were performed, with systematic variation of the following variables:

  • Bentonite material (“MX-80” or “Montigel”)
  • Water-to-solid mass ratio (7% — 33%)
  • Dry density (1.3 g/m3 — 2.1 g/m3 )
  • Diffusing salt (SrCl2, SrI2, CsCl, CsI, UO2(NO3)2, Th(NO3)4, KCl, KI, KNO3, K2SO4, K2CO3, KF)

Distribution of water in the samples

From e.g. X-ray diffraction (XRD) we know that bentonite water at low water content is distributed in distinct, sub-nm thin films. For simplicity we will refer to all water in the samples as interlayer water, although some of it, reasonably, forms interfaces with air. The relevant point is that the samples contain no bulk water phase, but only interfacial (interlayer) water.

I argue extensively on this blog for that interlayer water is the only relevant water phase also in saturated samples under pressure. In the present case, however, it is easier to prove that this is the case, as the samples are merely pressed bentonite powder at a certain water content; the bentonite water is not pressurized, the samples are not exposed to liquid bulk water, nor are they in equilibrium with liquid bulk water. Since the water in the samples obviously is mobile — as vapor, but most reasonably also in interconnected interlayers — it is a thermodynamic consequence that it distributes as to minimize the chemical potential.

There is a ton of literature on how the montmorillonite basal spacing varies with water content. Here, we use the neat result from Holmboe et al. (2012) that the average interlayer distance varies basically linearly2 with water content, like this

average basal distance vs. water content from Holmboe et al. (2012)

XRD-studies also show that bentonite water is distributed in rather distinct hydration states, corresponding to 0, 1, 2, or 3 monolayers of water.3 We label these states 0WL, 1WL, 2WL, and 3WL, respectively. In the figure is indicated the approximate basal distances for pure 1WL (12.4 Å), 2WL (15.7 Å), and 3WL (19.0 Å), which correspond roughly to water-to-solid mass ratios of 0.1, 0.2, and 0.3, respectively.

From the above plot, we estimate roughly that the driest samples in Kahr et al. (1985) (\(w \sim 0.1\)) are in pure 1WL states, then transitions to a mixture of 1WL and 2WL states (\(w\sim 0.1 – 0.2\)), to pure 2WL states (\(w \sim 0.2\)), to a mixture of 2WL and 3WL states (\(w\sim 0.2 – 0.3\)), and finally to pure 3WL states (\(w\sim 0.3\)).

Results

With the knowledge of how water is distributed in the samples, let’s take a look at the results of Kahr et al. (1985).

Mobility of interlayer cations confirmed

The most remarkable results are of qualitative character. It is, for instance, demonstrated that several cations diffuse far into the samples. Since the samples only contain interlayer water, this is a direct proof of ion mobility in the interlayers!

Also, cations are demonstrated to be mobile even when the water content is as low as 7 or 10 %! As such samples are dominated by 1WL states, this is consequently evidence for ion mobility in 1WL states.

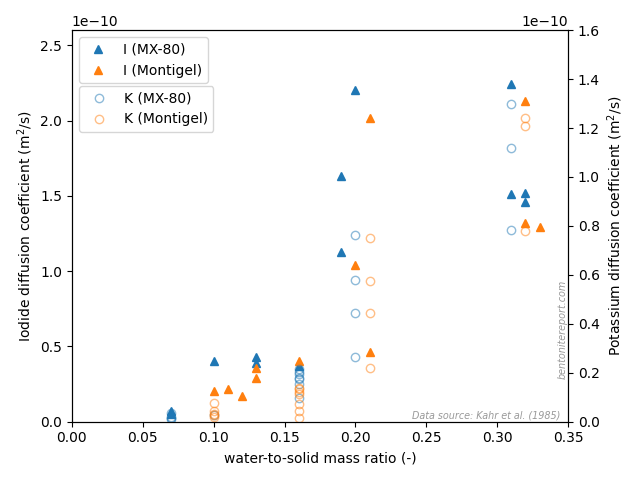
A more quantitative assessment furthermore shows that the cation diffusivities varies with water content in an almost step-wise manner, corresponding neatly to the transitions between various hydration states. Here is the data for potassium and strontium

De vs. water content for potassium and strontium from Kahr et al. (1985)

This behavior further confirms that the ions diffuse in interlayers, with an increasing diffusivity as the interlayers widen.

It should also be noted that the evaluated values of the diffusivities are comparable to — or even larger4 — than corresponding results from saturated, pressurized tests. This strongly suggests that interlayer diffusivity dominates also in the latter types of tests, which also has been confirmed in more recent years. The larger implication is that interlayer diffusion is the only relevant type of diffusion in general in compacted bentonite.

Anions enter interlayers (and are mobile)

The results also clearly demonstrate that anions (iodide) diffuse in systems with water-to-solid mass ratio as low as 7%! With no other water around, this demonstrates that anions diffuse in — and consequently have access to — interlayers. This finding is strongly confirmed by comparing the \(w\)-dependence of diffusivity for anions and cations. Here is plotted the data for iodide and potassium (with the potassium diffusivity indicated on the right y-axis)

De vs. water content for iodide and potassium from Kahr et al. (1985)

The iodide mobility increases as the system transitions from 1WL to 2WL, in a very similar way as for potassium (and strontium). If this is not a proof that the anion diffuse in the same domain as the cation I don’t know what is! Also for iodide the value of the diffusivity is comparable to what is evaluated in water saturated systems under pressure, which implies that interlayer diffusivity dominates generally in compacted bentonite, also for anions.

Dependence of diffusivity on water content and density

A conclusion made in Kahr et al. (1985), that I am not sure I fully agree with, is that diffusivity mainly depends on water content rather than density. As seen in the diagrams above, the spread in diffusivity is quite substantial for a given value of \(w\). There is actually some systematic variation here: for constant \(w\), diffusivity tend to increase with dry density.

Although using unsaturated samples introduces additional variation, the present study provides a convenient procedure to study diffusion in systems with very low water content. A more conventional set-up in this density limit has to deal with enormous pressures (on the order of 100 MPa).

Interlayer chemistry

An additional result is not acknowledged in the report, but is a direct consequence of the observations: the tests demonstrate that interlayers are chemically active. The initially solid salt evidently dissolves before being able to diffuse. Since these samples are not even close to containing a bulk water phase (as discussed above), the dissolution process must occur in an interlayer. More precisely, the salt must dissolve in interface water between the salt mineral and individual montmorillonite layers, as illustrated here

Schematics of KI dissolution in interlayer water

This study seems to have made no impact at all

In the beginning of 1985, the research community devoted to radioactive waste barriers seems to have been on its way to correctly identify diffusion in interlayers as the main transport mechanism, and to recognize how ion diffusion in bentonite is influenced by equilibrium with external solutions.

Already in 1981, Torstenfelt et al. (1981) concluded that the traditional diffusion-sorption model is not valid, for e.g. diffusion of Sr and Cs, in compacted bentonite. They also noted, seemingly without realizing the full importance, that these ions diffused even in unsaturated samples with as low water-to-solid mass ratio as 10%.

A significant diffusion was observed for Sr in dry clay, although slower than for water saturated clay, Figure 4, while Cs was almost immobile in the dry clay.

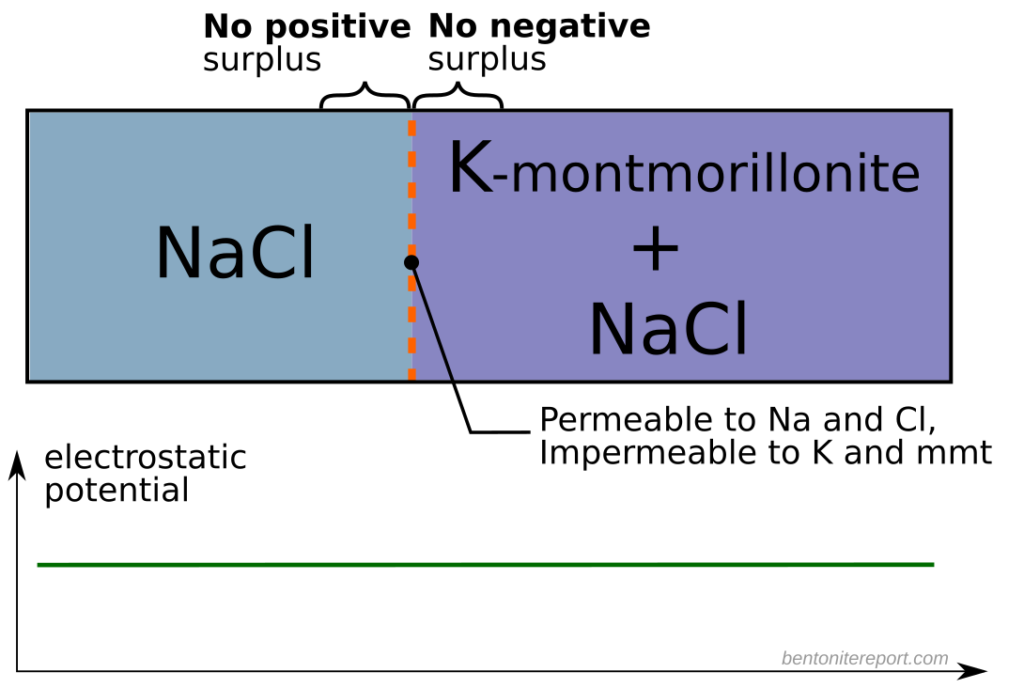
A year later also Eriksen and Jacobsson (1982) concluded that the traditional diffusion model is not valid. They furthermore pointed out the subtleties involved when interpreting through-diffusion experiments, due to ion equilibrium effects

One difficulty in correlating the diffusivities obtained from profile analysis to the diffusivities calculated from steady state transport data is the lack of knowledge of the tracer concentration at the solution-bentonite interface. This concentration is generally higher for sorbing species like positive ions (counterions to the bentonite) and lower for negative ions (coions to the bentonite) as shown schematically in figure 11. The equilibrium concentration of any ion in the bentonite and solution respectively is a function of the ionic charge, the ionic strength of the solution and the overall exchanger composition and thereby not readily calculated

In Eriksen and Jacobsson (1984) the picture is fully clear

By regarding the clay-gel as a concentrated electrolytic system Marinsky has calculated (30) distribution coefficients for Sr2+ and Cs+ ions in good agreement with experimentally determined Kd-values. The low anionic exchange capacity and hence the low anion concentration in the pore solution caused by Donnan exclusion also explain the low concentrations of anionic tracers within the clay-gel

[…]

For simple cations the ion-exchange process is dominating and there is, as also pointed out by Marinsky (30), no need to suppose that the counterions are immobilized. It ought to be emphasized that for the compacted bentonite used in the diffusion experiments discussed in this report the water content corresponds roughly to 2-4 water molecule layers (31). There is therefore really no “free water” and the measured diffusivity \(\bar{D}\) can be regarded as corresponding approximately to the diffusivity within the adsorbed phase […]

Furthermore, also Soudek et al. (1984) had discarded the traditional diffusion-sorption model, identified the exchangeable cations as giving a dominating contribution to mass transfer, and used Donnan equilibrium calculations to account for the suppressed internal chloride concentration.

In light of this state of the research front, the contribution of Kahr et al. (1985) cannot be described as anything but optimal. In contrast to basically all earlier studies, this work provides systematic variation of several variables (most notably, the water-to-solid ratio). As a consequence, the results provide a profound confirmation of the view described by Eriksen and Jacobsson (1984) above, i.e. that interlayer pores essentially govern all physico-chemical behavior in compacted bentonite. A similar description was later given by Bucher and Müller-Vonmoos (1989) (though I don’t agree with all the detailed statements here)

There is no free pore water in highly compacted bentonite. The water in the interlayer space of montmorillonite has properties that are quite different from those of free pore water; this explains the extremely high swelling pressures that are generated. The water molecules in the interlayer space are less mobile than their free counterparts, and their dielectric constant is lower. The water and the exchangeable cations in the interlayer space can be compared to a concentrated salt solution. The sodium content of the interlayer water, at a water content of 25%, corresponds approximately to a 3-n salt solution, or six times the concentration in natural seawater. This more or less ordered water is fundamentally different from that which engineers usually take into account; in the latter case, pore water in a saturated soil is considered as a freely flowing fluid. References to the porosity in highly compacted bentonite are therefore misleading. Highly compacted bentonite is an unfamiliar material to the engineer.

Given this state of the research field in the mid-80s, I find it remarkable that history took a different turn. It appears as the results of Kahr et al. (1985) made no impact at all (it may be noticed that they themselves analyzed the results in terms of the traditional diffusion-sorption model). And rather than that researchers began identifying that transport in interlayers is the only relevant contribution, the so-called surface diffusion model gained popularity (it was already promoted by e.g. Soudek et al. (1984) and Neretnieks and Rasmuson (1983)). Although this model emphasizes mobility of the exchangeable cations, it is still centered around the idea that compacted bentonite contains bulk water.5 Most modern bentonite models suffer from similar flaws: they are formulated in terms of bulk water, while many effects related to interlayers are treated as irrelevant or optional.

For the case of anion diffusion the historical evolution is maybe even more disheartening. In 1985 the notions of “effective” or “anion-accessible” porosities seem to not have been that widely spread, and here was clear-cut evidence of anions occupying interlayer pores. But just a few years later the idea began to grow that the pore space in compacted bentonite should be divided into regions which are either accessible or inaccessible to anions. As far as I am aware, the first use of the term “effective porosity” in this context was used by Muurinen et al. (1988), who, ironically, seem to have misinterpreted the Donnan equilibrium approach presented by Soudek et al. (1984). To this day, this flawed concept is central in many descriptions of compacted clay.

Footnotes

[1] “Ion diffusion in highly compacted bentonite”

[2] Incidentally, the slope of this line corresponds to a water “density” of 1.0 g/cm3.

[3] This is the region of swelling often referred to as “crystalline”.

[4] I’m not sure the evaluation in Kahr et al. (1985) is fully correct. They use the solution to the diffusion equation for an impulse source (a Gaussian), but, to my mind, the source is rather one of constant concentration (set by the solubility of the salt). Unless I have misunderstood, the mathematical expression to be fitted to data should then be an erfc-function, rather than a Gaussian. Although this modification would change the numerical values of the evaluated diffusion coefficients somewhat, it does not at all influence the qualitative insights provided by the study.

[5] I have discussed the surface diffusion model in some detail in previous blog posts.

The mechanism for “anion” exclusion

Leave a reply

Repulsion between surfaces and anions is not really the point

Many publications dealing with “anion” exclusion in compacted bentonite describe the phenomenon as being primarily due to electrostatic repulsion of anions from the negatively charged clay surfaces. This explanation, which may seem plausible both at a first and a second glance, is actually not that satisfactory. There are two major issues to consider:

  • Although it is popular to use the word “anion” when referring to the phenomenon, it must be remembered that the anions are accompanied by cations, in order to maintain overall charge neutrality; it really is salt that is excluded from the bentonite. This observation shows that the above “explanation” is incomplete: it can be argued with the same logic that salt should accumulate, because the clay surfaces attract the cations of the external salt.
  • Salt exclusion occurs generally in Donnan systems, also in those that lack surfaces. Its principal explanation can consequently not involve the presence of surfaces. For a simpler system, e.g. potassium ferrocyanide, the “explanation” above translates to claiming that exclusion is caused by “anions” being electrostatically repelled by the ferrocyanide ions. In this case it may be easier to spot the shortcoming of such a claim, and to consider also the potassium ions (which attract anions), as well as the role played by the cations of the excluded salt.

What, then, is the primary cause for salt exclusion? Let us continue with using potassium ferrocyanide as an example of a simple Donnan system, and then translate our findings to the case of compacted bentonite.

Ferrocyanide

Consider a potassium ferrocyanide solution separated from a potassium chloride solution by a membrane permeable to all but the ferrocyanide ions. The ionic configuration near the membrane then looks something like this

KCl - Ferrocyanide interface and potential variation

Because potassium ions can pass the membrane, and because they have an entropic driving force to migrate out of the ferrocyanide solution, a (microscopic) region is formed in the external solution next to the membrane, with an excess amount of positive charge. Similarly, a region is formed next to the membrane in the ferrocyanide solution with an excess amount of negative charge. Thus, a region of charge separation exists across the membrane — similar to the depletion zone in a p-n junction — over which the electrostatic potential varies. The electric field (= a varying potential) at the interface acts as to pull back potassium ions towards the ferrocyanide solution. The equilibrium width of the space charge region is set when the diffusive flux is balanced by the flux due to the electric field.

With a qualitative understanding of the electrostatic potential configuration we can now give the most plain answer to what causes “anion” exclusion: it is because of the potential difference across the membrane. Chloride ions behave in the opposite way as compared to potassium, with an entropic driving force to enter the ferrocyanide solution, while being pulled back towards the external solution due to the electric field across the membrane.

Here the mindful reader may perhaps object and point out that the electric field restricting the chloride inflow reasonably originates from the ferrocyanide anions. It thus may seem that “anion” exclusion, after all, is caused by repulsion from other negative charges.

Indeed, electrostatic repulsion of anions requires the “push” of some other negatively charged entity. But note that the potential is constant in the interior of the ferrocyanide solution, and only varies near the membrane. The variation of the potential is caused by separation of charge: chloride is as much “pushed” out of the ferrocyanide solution by the ferrocyanide as it is “pulled” out of it, due to electrostatic attraction, by the excess potassium on the other side. Repulsion between charges of equal sign occurs also in the interior of the ferrocyanide solution (or in any ionic solution), but does not in itself lead to salt exclusion.

Bentonite

The above description can be directly transferred to the case of compacted bentonite. Replacing the potassium ferrocyanide with e.g. K-montmorillonite, salt exclusion occurs mainly because potassium can migrate out of the clay region, while montmorillonite particles cannot. Again, we have charge separation with a resulting varying electrostatic potential across the interface.

Admittedly, the general situation is more complicated in bentonite because of the extension of montmorillonite particles; viewed as “anions”, these are irregularly shaped macromolecules with hundreds or thousands of charge centers.

The ion configuration in a bentonite suspension therefore looks quite different from a corresponding ordinary solution, as the montmorillonite charge obviously is constrained to individual particles. Dilute systems thus have charge separation on the particle scale and show salt exclusion even without charge separation at the interface to the external solution. These types of systems (suspensions) have historically been the subject of most studies on “anion” exclusion, and are usually treated theoretically using the Gouy-Chapman model.

With increasing density, however, the effect of a varying potential between montmorillonite particles diminishes, while the effect of charge separation at the interface increases. For dense systems (> 1.2 g/cm3, say), we may therefore approximate the internal potential as constant and only consider the variation across the interface to the external solution using Donnan’s “classical” framework.1

Here is an illustration of the validity of this approximation:

Internal and external potential in compacted bentonite system

The figure shows the difference between the external (green) and the average internal (orange) potentials in a 1:1 system of density 1.3 g/cm3 and with external concentration 0.1 M, calculated using Donnan’s “classical” equation. Also plotted is the electrostatic potential across the interlayer (blue) as calculated using the Poisson-Boltzmann equation,2 in a similar system (interlayer distance 1 nm). It is clear that the variation of the Poisson-Boltzmann potential from the average is small in comparison with the Donnan potential.

Repulsion between chloride and montmorillonite particles of course occurs everywhere in compacted bentonite, whereas the phenomenon mainly responsible for salt exclusion occurs only near the interfaces. Merely stating electrostatic repulsion as the cause for salt exclusion in compacted bentonite does not suffice, just as in the case of ferrocyanide.

To illustrate that the salt exclusion effect depends critically on exchangeable cations being able to diffuse out of the bentonite, consider the following thought experiment.3 Compacted K-montmorillonite is contacted with a NaCl solution. But rather than having a conventional component separating the solution and the clay, we imagine a membrane that does not allow for the passage of neither potassium nor clay, but that allows for the passage of sodium and chloride. Since potassium is not allowed to diffuse out of the bentonite, no charge separation occurs across the membrane. With no space charge region, the electrostatic potential does not vary and NaCl is not excluded! (to the extent that the Donnan approximation is valid)

NaCl + K-montmorillonite with interface only permeable for Na and Cl

A charge neutral perspective

The explanation for “anion” exclusion that we have explored rests on the formation of a potential difference across the interface region between bentonite and external solution. But remember that it is salt — in our example KCl — that is excluded from the bentonite (or the ferrocyanide solution), and that the cation (K) gains energy by being transferred from the external to the internal solution. The electrical work for transferring a unit of KCl is thus zero (which makes sense since KCl is a charge neutral entity). In this light, it may seem unsatisfactory to offer the potential difference as the sole explanation for salt exclusion.

I therefore think that the following kinematic way of reasoning is very helpful. Instead of considering the mass transfer of Cl across the membrane in terms of oppositely directed “electric” and “diffusive” parts, we lump them together with equal amounts of K transfer, giving two equal but oppositely directed fluxes of KCl. Reasonably, the KCl flux into the ferrocyanide solution is proportional to the external ion concentrations

\begin{equation} j^\mathrm{in}_\mathrm{KCl} = A\cdot c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} \end{equation}

while the outflux is proportional to the internal ion concentrations

\begin{equation} j^\mathrm{out}_\mathrm{KCl} = -A\cdot c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

\(A\) is a coefficient accounting for the transfer resistance across the interface region. Requiring the sum of these fluxes to be zero gives the following relation

\begin{equation} c_\mathrm{K}^\mathrm{ext}\cdot c_\mathrm{Cl}^\mathrm{ext} = c_\mathrm{K}^\mathrm{int}\cdot c_\mathrm{Cl}^\mathrm{int} \end{equation}

which is the (ideal) Donnan equation.

We can therefore interpret KCl exclusion as an effect of potassium in the clay providing a potential for “out-transfer”, as soon as the chance is given, i.e. when chloride enters from the external solution. From this perspective salt exclusion could maybe be said to be a form of cation “rejection”.

Footnotes

[1] Note also that the Gouy-Chapman model is not valid in the high density limit, although it is applied (or alluded to) in this limit in many publications. But e.g. Schofield (1947) states (about the Gouy-Chapman solution):

[T]he equation is applicable to cases in which the distance between opposing surfaces considerably exceeds the distance between neighboring point charges on the surfaces; for there will then be a range of electrolyte concentrations over which the radius of the ionic atmosphere is less than the former and greater than the latter.

This criterion is not met in compacted bentonite, where instead the interlayer distance is comparable to the distance between neighboring charge centers on the surfaces. Invalid application of the Gouy-Chapman model also seems to underlie the flawed but widespread “anion-accessible porosity” concept.

[2] This calculation uses the equations presented in Engström and Wennerström (1978), and assumes no excess ions and a surface charge density of 0.111 \(\mathrm{C/m^2}\). For real consistency this calculation should really be performed with the boundary condition of 0.1 M external concentration. However, since the purpose of the graph is just to demonstrate the sizes of the two potential variations, and since I have yet to acquire a reasonable tool for performing Poisson-Boltzmann calculations with non-zero external concentration, I disregard this inconsistency. Moreover, the continuum assumption of the Poisson-Boltzmann description is anyway beginning to lose its validity at these interlayer distances. Update (220831): Solutions to the Poisson-Boltzmann equation with non-zero external concentration are presented here.

[3] Perhaps this could be done as a Molecular Dynamics simulation?