In a previous blog post, we discussed how the diffusivity of simple cations1 has a small, or even negligible, dependence on background concentration (or, equivalently, on \(K_d\)), and how this observation motivates modeling compacted bentonite as a homogeneous system, containing only interlayer pores.
Despite the indisputable fact that “\(D_a\)”2 for simple ions does not depend much on \(K_d\), the results have seldom been modeled using a homogeneous bentonite model. Instead there are numerous attempts in the bentonite literature to both measure and model a variation of “\(D_a\)” with \(K_d\), usually with a conclusion (or implication) that “\(D_a\)” depends significantly on \(K_d\). In this post we re-examine some of these studies.
The claimed \(K_d\)-dependency is often “supported” by the so-called surface diffusion model. I have previously shown that this model is incorrect.3 Here we don’t concern ourselves with the inconsistencies, but just accept the resulting expression as the model to which authors claim to fit data. This model expression is
\begin{equation} D_a = \frac{D_p + \frac{\rho K_d}{\phi} D_s}{1+\frac{\rho K_d}{\phi}} \tag{1} \end{equation}
where \(D_p\) and \(D_s\) are individual domain diffusivities for bulk water and surface regions, respectively, \(\rho\) is dry density, \(\phi\) porosity, and \(K_d\), of course, is assumed to quantify the distribution of ions between bulk water and surfaces as \(s = K_d\cdot c^\mathrm{bulk}\), where \(s\) is the amount of ions on the surface (per unit dry mass), and \(c^\mathrm{bulk}\) is the corresponding bulk water concentration.
Muurinen et al. (1985)
Muurinen et al. (1985) measured diffusivity in high density bentonite samples at various background concentrations, using a type of closed-cell set-up. They also measured corresponding values of \(K_d\) in batch “sorption” tests. The results for cesium, in samples with density in the range \(1870 \;\mathrm{kg/m^3}\) — \(2030 \;\mathrm{kg/m^3}\), are presented in the article in a figure similar to this:
The markers show experimental data, and the solid curve shows the model (eq. 1) with \(D_p = 1.2 \cdot 10^{-10}\;\mathrm{m^2/s}\)4 and \(D_s = 4.3\cdot 10^{-13}\;\mathrm{m^2/s}\).
The published plot may give the impression of a systematic variation of \(D_a\) for cesium, and that this variation is captured by the model. But the data is plotted with a logarithmic y-axis, which certainly is not motivated. Let’s see how the plot looks with a linear y-axis (we keep the logarithmic x-axis, to clearly see the model variation).
Now the impression is quite different: this way of plotting reveals that the experimental data only cover a part where the model does not vary significantly. With the adopted range on the x-axis (as used in the article) we actually don’t see the full variation of the model curve. Extending the x-axis gives the full picture:
With the full model variation exposed, it is evident that the model fits the data only in a most superficial way. The model “fits” only because it has insignificant \(K_d\)-dependency in the covered range, in similarity with the measurements.
The defining feature of the model is that the diffusivity is supposed to transition from one specific value at high \(K_d\), to a significantly different value at low \(K_d\). As no such transition is indicated in the data, the above “fit” does not validate the model.
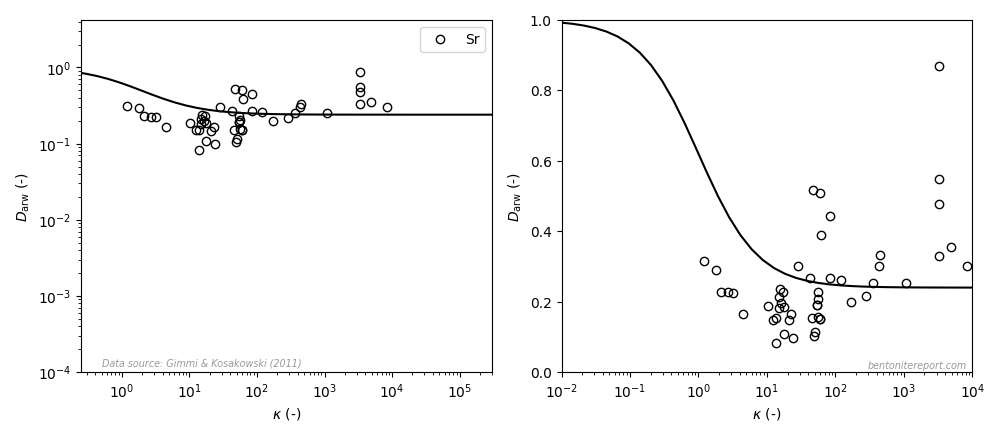
Muurinen et al. (1985) also measured diffusion of strontium in two samples of density \(1740 \;\mathrm{kg/m^3}\). The figures below show the data and corresponding model curve.
The left diagram is similar to how the data is presented in the article, while the right diagram utilizes a linear y-axis and shows the full model variation. The line shows the surface diffusion model with parameters \(D_p = 1.2 \cdot 10^{-10}\;\mathrm{m^2/s}\) and \(D_s = 8.8 \cdot 10^{-12}\;\mathrm{m^2/s}\). In this case it is clear even from the published plot that the experimental data shows no significant variation.
The only reasonable conclusion to make from the above data is that cesium and strontium diffusivity does not significantly depend on \(K_d\) (which implies a homogeneous system). This is actually also done in the article:
The apparent diffusivities of strontium and cesium do not change much when the salt concentration used for the saturation of the samples is changed and the sorption factors change. The surface diffusion model agrees fairly well with the observed diffusion-sorption behaviour.
I agree with the first sentence but not with the second. In my mind, the two sentences contradict each other. From the above plots, however, it is trivial to see that the surface diffusion model does not agree (in any reasonable sense) with observations.
Eriksen et al. (1999)
Although Muurinen et al. (1985) concluded insignificant \(K_d\)-dependency on the diffusion coefficients for strontium and cesium, researchers have continued throughout the years to fit the surface diffusion model to experimental data on these and other ions.
Eriksen et al. (1999) present old and new diffusion data for strontium and cesium (and sodium), fitted and plotted in the same way as in Muurinen et al. (1985). Here are the evaluated diffusivities for cesium plotted against evaluated \(K_d\), as presented in the article, and re-plotted in different ways with a linear y-scale:
The curve shows the surface diffusion model (eq. 1), with parameters \(D_p = 8 \cdot 10^{-10}\;\mathrm{m^2/s}\) and \(D_s = 6 \cdot 10^{-13}\;\mathrm{m^2/s}\). The points labeled “Eriksen 99” are original data obtained from through-diffusion tests on “MX-80” bentonite at dry density 1800 \(\mathrm{kg/m^3}\).5 The source for the data points labeled “Muurinen 94” is the PhD thesis of A. Muurinen.6
The upper left plot shows the data as presented in the article; again, a logarithmic y-axis is used. In this case, a zoomed-in view with a linear y-axis (upper right diagram) may still give the impression that the data has a systematic variation that is captured by the model. But viewing the whole range reveals that the model is fitted to data where variation is negligible (bottom diagrams), just as in Muurinen et al. (1985).
Data and model for strontium presented in Eriksen et al. (1999) look like this:
The model (line) has parameters \(D_p = 3 \cdot 10^{-10}\;\mathrm{m^2/s}\) and \(D_s = 1 \cdot 10^{-11}\;\mathrm{m^2/s}\), and the source for the data points labeled “Eriksen 84” is found here.
In this case, not even the diagram presented in the article (left) seems to support the promoted model. This is also confirmed when utilizing a linear y-axis, and showing the full model variation (right diagram).
Eriksen et al. (1999) conclude that strontium diffusivities are basically independent of \(K_d\), but claim, in contrast to Muurinen et al. (1985), that cesium diffusivity depends significantly on \(K_d\):
[I]n the \(K_d\) interval 0.01 to 1 the apparent \(\mathrm{Cs}^+\) diffusivity decreases by approximately one order of magnitude whereas for \(\mathrm{Na}^+\) and \(\mathrm{Sr}^{2+}\) the apparent diffusivity is virtually constant.
They also claim that the surface diffusion model fits the data:
\(D_\mathrm{a}\) curves for \(\mathrm{Cs}^+\) and \(\mathrm{Sr}^{2+}\), calculated using a Eq. (6) [eq. 1 here], are plotted in Fig. 4. As can be seen, good fits to experimental data were obtained […]
Note that the variation in the model for cesium is motivated by three data points with relatively high diffusivity and basically the same \(K_d \sim 0.05\;\mathrm{m^3/kg}\). It seems like the model has been fitted to these points, while the point at \(K_d \sim 0.02\;\mathrm{m^3/kg}\) has been mainly neglected. The resulting model has a huge bulk water diffusivity (\(D_p\)), which is about 7 times larger than in the corresponding fit in Muurinen et al. (1985), and only 2.5 times smaller than the diffusivity for cesium in pure water.
Note that, if you claim that the surface diffusion model fits in this case, you implicitly claim that the observed variation — which still is negligible on the scale of the full model variation — is caused by the influence of this enormous (for a 1800 \(\mathrm{kg/m^3}\) sample) bulk pore water diffusivity; with a more “reasonable” value for \(D_p\), the model no longer fits. There are consequently valid reasons to doubt that the claimed \(K_d\) dependence is real. We will return to this fit in the next section.
Gimmi & Kosakowski (2011)
We have now seen several examples of authors erroneously claiming (or implying) that a surface diffusion model is valid, when the actual data for “\(D_a\)” has no significant \(K_d\)-dependency. For reasons I cannot get my head around, this flawed treatment is still in play.
Rather than identifying the obvious problem with the previously presented fits, Gimmi and Kosakowski (2011) instead extended the idea of expressing the diffusivity as a function of \(K_d\) by using scaled, dimensionless quantities
\begin{equation} D_\mathrm{arw} = \frac{D_\mathrm{a}\tau_w}{D_0} \tag{2} \end{equation}
\begin{equation} \kappa = \frac{\rho K_d}{\phi} \end{equation}
where \(D_0\) is the corresponding diffusivity in pure water and \(\tau_w\) is the “tortuosity factor” for water in the system of interest. This factor is simply the ratio between the water diffusivity in the system of interest and the water diffusivity in pure water (I have written about the problem with factors like this here).
The idea — it seems — is that using \(D_\mathrm{arw}\) and \(\kappa\) as variables should make it possible to directly compare the mobility of a given species in systems differing in density, clay content, etc.
Even though it makes some sense that the diffusivity of a specific species scales with the diffusivity of water in the same system, the above procedure inevitably introduces more variation in the data — both because an additional measured quantity (water diffusivity) is involved when evaluating the scaled diffusivity, but also because water diffusivity may depend differently on density as compared with the diffusivity of the species under study.
Also Gimmi and Kosakowski (2011) use the flawed surface diffusion model for analysis, and their expression for \(D_\mathrm{arw}\) is
\begin{equation} D_\mathrm{arw} = \frac{1+\mu_s\kappa}{1+\kappa} \tag{3} \end{equation}
where \(\mu_s = D_s\tau_w/D_0\) is a “relative surface mobility”. This equation is obtained from eq. 1, by dividing by \(D_p\) and assuming \(D_p = D_0/\tau_w\).
Gimmi and Kosakowski (2011) fit eq. 3 to a large set of collected data, measured in various types of material, including bentonites, clay rocks, and clayey soils. This is their result for cesium7 (the model curve is eq. 3 with \(\mu_s = 0.031\)8)

Viewed as a whole, this data is more scattered as compared with the previous studies. This is reasonably an effect of the larger diversity of the samples, but also an effect of multiplying the “raw” diffusion coefficient with the factor \(\tau_w\) (eq. 2).
Just as in the previous studies we have looked at, the published plot (similar to the left diagram) may give the impression of a systematic variation of the diffusivity with \(K_d\) (it contains partly the same data). But just as before, a linear y-axis (right diagram) reveals that the model is fitted only to data where variation is negligible.
Note that the three data points that contributed to the majority of the variation in the fitted model in Eriksen et al. (1999) here appear as outliers.9 The variation with \(K_d\) for cesium claimed in that study is thus invalidated by this larger data set.
As we have noted already, the only reasonable conclusion to draw from this data is that there is no systematic \(K_d\)-dependency on diffusivity of cesium or strontium, and that it does not — in any reasonable sense — fit the surface diffusion model. Yet, also Gimmi and Kosakowski (2011) imply that the surface diffusion is valid:
The data presented here show a general agreement with a simple surface diffusion model, especially when considering the large errors associated with the \(D_\mathrm{erw}\) and \(D_\mathrm{arw}\).
This paper, however, contains an even worse “fit” to strontium data, as compared to the earlier studies (the left diagram is similar to the how it is presented in the article, the right diagram uses a linear y-axis; the line is eq. 3 with \(\mu_s = 0.24\)8):
This data does not suggest a variation in accordance with the adopted model even when plotted in a log-log diagram. With a linear y-axis, the dependence rather seems to be the opposite: \(D_\mathrm{arw}\) appears to increase with \(\kappa\). However, I suspect that this is a not a “real” dependence, but rather an effect of trying to construct a “relative” diffusivity; note that while \(\kappa\) spans four orders of magnitude, \(D_\mathrm{arw}\) scatters only by a factor of 5 or 6. Nevertheless, how this data can be claimed to show “general agreement” with the surface diffusion model is a mystery to me.
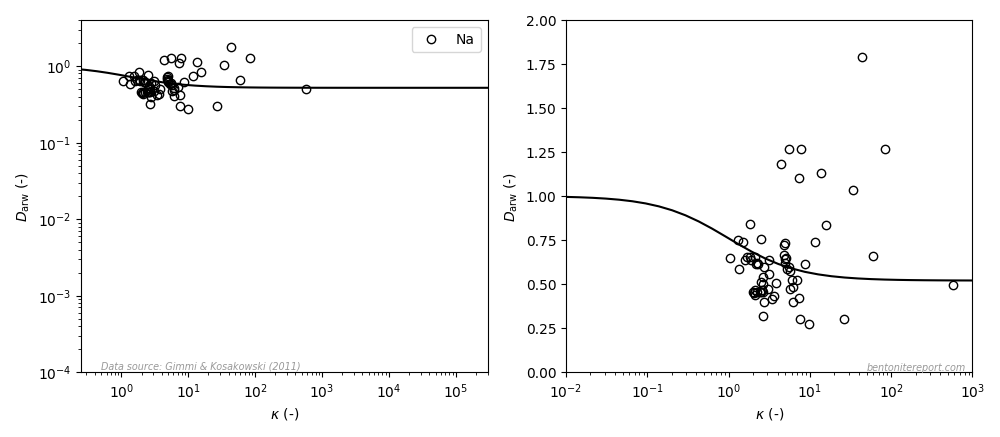
The view is similar for sodium (the left diagram is similar to the how it is presented in the article, the right diagram uses a linear y-axis; the line is eq. 3 with \(\mu_s=0.52\)8):
Even if the model in this case only displays minor variation, it can hardly be claimed to fit the data: again, the data suggests a diffusivity that increases with \(\kappa\). But a significant amount of these data points have \(D_\mathrm{arw} > 1\), which is not likely to be true, as it indicates that the relative mobility for sodium is larger than for water. Consequently, the major contribution of the variation seen in this data is most probably noise.
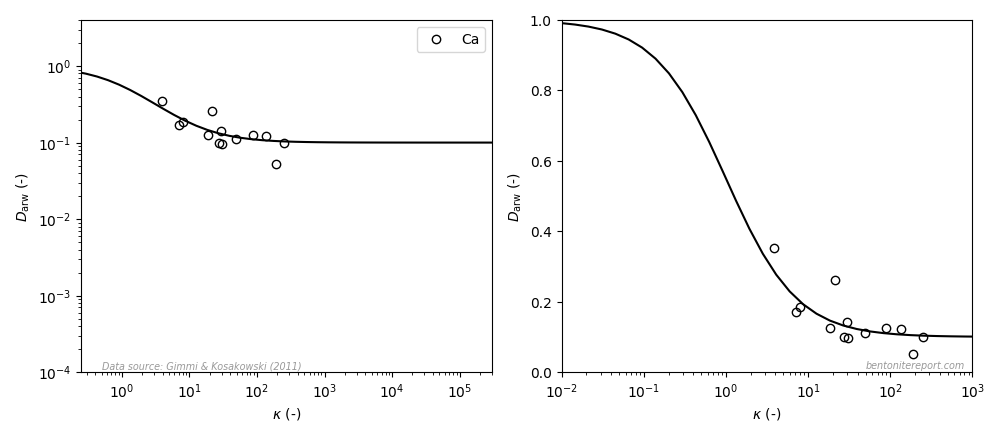
Gimmi and Kosakowski (2011) also examined diffusivity for calcium, and the data looks like this (the left diagram is similar to the how it is presented in the article, the right diagram uses a linear y-axis; the line is eq. 3 with \(\mu_s=0.1\)8):
Here it looks like the data, to some extent, behaves in accordance with the model also when plotted with linear y-axis covering the full model variation. However, there are significantly less data reported for calcium (as compared with cesium, strontium, and sodium) and the model variation is supported only by a few data points10. I therefore put my bet on that if calcium diffusivity is studied in more detail, the dependence suggested by the above plot will turn out to be spurious.11
Some thoughts
I am more than convinced that the only reasonable starting point for modeling saturated bentonite is a homogeneous description. I had nevertheless expected to at least have to come up with an argument against the multi-porous view put forward in the considered publications (and in many others). I am therefore quite surprised to find that this argument is already provided by the data in the very same publications (and even by the statements, sometimes): there is nothing in the data here reviewed that seriously suggests that cation diffusion is influenced by a heterogeneous pore structure.
Still, the unsupported idea that cations in compacted bentonite are supposed to diffuse in two (or more) different types of water domains has evidently propagated through the scientific literature for decades, and a multi-porous view is mainstream in modern bentonite research. It is difficult to not feel disheartened when faced with this situation. What would it take for researchers to begin scrutinize their assumptions? Is nobody interested in the topics we are supposed to study?
Footnotes
[1] Unfortunately, a quantity which by many is incorrectly interpreted as an “apparent” diffusivity.
[2] I use quotation marks to indicate that \(D_a\) is a parameter in the traditional diffusion-sorption model, a model not valid for compacted bentonite. Still, this parameter is often reported as if it was a directly measured quantity.
[3] I have also derived a correct version of the surface diffusion model, which does not involve apparent diffusivity.
[4] The article states \(\epsilon D_p = 3.5\cdot 10^{-11}\; \mathrm{m^2/s}\), where \(\epsilon\) is the porosity. \(D_p = 1.2\cdot 10^{-10} \; \mathrm{m^2/s}\) corresponds to \(\epsilon = 0.29\).
[5] In this study, both \(K_d\) and \(D_a\) were evaluated by fitting the traditional diffusion-sorption model to concentration measurements.
[6] I have had no access to this document, and I have not verified e.g. sample density (this data set is different from that presented in the previous section). Instead, I have read these values from the diagram in Eriksen et al. (1999).
[7] They actually divide their cesium data into two categories, which show quite different mobility. The data shown here — which includes bentonite samples — is for systems categorized as being “non-illite” or having Cs concentration above “trace”.
[8] According to the article table, the fitted values for \(\mu_s\) are 0.52 (Na), 0.39 (Sr), 0.087 (Ca), and 0.015 (Cs). The plotted lines, however, appear to instead use what is listed as “mean \(\mu_s\)”. Here, I have used these \(\mu_s\)-values: 0.52 (Na), 0.24 (Sr), 0.1 (Ca), and 0.031 (Cs).
[9] This cluster contains a fourth data point, from Jensen and Radke (1988).
[10] All data for calcium is essentially from only two different sources: Staunton (1990) and Oscarsson (1994).
[11] It would also be more than amazing if it turns out — after it is verified that Cs, Na, and (especially) Sr show no significant \(K_d\) dependence — that Ca diffusivity actually varies in accordance with the flawed surface-diffusion model!