Monthly Archives: September 2020

Anion-accessible porosity – a brief history

2 Replies

Genesis

In the beginning there was the Poisson-Boltzmann equation. Solving it for the case of a salt solution in contact with a negatively charged plane surface (a.k.a. the Gouy-Chapman model) gives the concentration of cations and anions in the solution as a function of the distance to the surface, like this1

Illustration of Gouy-Chapman concentration profiles

Note:

  1. The suppression of the anion concentration near the surface is often referred to as negative adsorption or anion exclusion. The total amount of excluded anions per unit surface area (indicated in green), usually labeled \(\Gamma^-\), is obtained by integrating the Poisson-Boltzmann equation.
  2. There are, nevertheless, anions everywhere! This model will give zero anion concentration only for an infinitely negative electrostatic potential (or if \(c_0 = 0\), of course).

A clever way to utilize negative adsorption is for estimating the amount of smectite surface area in a soil sample, first suggested by Schofield (1947). This is done by comparing measured values of negative adsorption with the appropriate expression evaluated from the Gouy-Chapman model. When doing the necessary math2 for such an analysis you naturally end up with expressions like

\begin{equation} \frac{\Gamma^-}{c_0} \sim \text{const.}\cdot \kappa^{-1} \tag{1} \end{equation}

where \(c_0\) is the external anion concentration (i.e. far from the surface), and \(\kappa^{-1}\) is the Debye length. This equation, having the dimension of length, can be interpreted as the width, \(d_{ex}\), of a region devoid of anions, which gives the same amount of negative adsorption as the full exclusion region, as illustrated here (yellow)

Illustration exclusion distance

However, note:

  1. This is just an equivalent, fictitious region.
  2. Anions are still everywhere!

Due to its convenience in the analysis, the notion of an equivalent region devoid of anions — often referred to in terms of “volume of exclusion” — became rather popular. At the same time, authors stopped emphasizing that this is a fictitious region. A clear example of such a transition is Edwards and Quirk (1962) who states that \(\Gamma^-/c_0\) “can be regarded as the surface depth from which chloride ions are excluded”, while in Edwards et al. (1965) the same quantity (multiplied by area) is referred to as “the volume from which chloride is excluded”. The latter statement is, strictly speaking, wrong: the actual volume from which anions are excluded is the entire region where the concentration deviates from \(c_0\), and the exclusion is only partial — there are anions everywhere!

Compacted bentonite

But the idea of an actual region devoid of anions seems to have stuck, and I believe that this influenced the interpretation of diffusion in compacted bentonite3 in terms of “effective porosity” or “anion accessible-porosity”. Concepts which, in turn, have motivated the idea that bentonite contains bulk water (“free water”, “pore water”).

The first example of this usage in studies of compacted bentonite, that I know of, is in Muurinen et al. (1988) reporting chloride through-diffusion in bentonite with various densities and background concentrations.

The tracer concentration of the porewater clearly depends on the compaction of bentonite and on the salt concentration of the circulating water. The effective porosity can even be less than one percent when the salt concentration is low and compaction high. Also, the diffusivities strongly depend on the density of bentonite and on the salt concentration.

The low tracer concentration in bentonite in the diffusion tests […] are indicative of ion-exclusion [5]. Ion-exclusion probably decreases the effective size of the pores, which changes the geometric factor, of bentonite and thus the apparent diffusivity. In addition to the geometric factor, the effective diffusivity takes into account the effective pore volume; thus, the dependence is even stronger.

“Effective porosity” has not been defined earlier in the article, so it is difficult to know precisely what the authors mean by the term. But it is relatively clear4 from the second paragraph that they explain the measured fluxes as being a result of a physical variation of the pore volume accessible to anions, rather than as a variation of the tracer concentration in a homogeneous system. This is also supported by their writing in the conclusions section: “The decreased pore size and porosity caused by ion-exclusion could at least qualitatively explain the dependence.”

However, the reference they provide (“[5]”) is Soudek et al. (1984), who calculate anion exclusion by means of — the Poisson-Boltzmann equation! (Which predicts anions everywhere.) In fact, Soudek et al. (1984) calculate what they term “Donnan exclusion” in a homogeneous model of “parallel, equally-spaced platelets”. Thus, the reference supplied by Muurinen et al. (1988) is in direct contradiction with their interpretation that the pore size and porosity is decreasing with the salt concentration.

Soudek et al. (1984) even provide an example of how the average chloride concentration between the platelets depends on the separation distance, when in equilibrium with an external solution of 10 mM, and write

Note the extremely strong rejection of the co-ion. At 50 w% clay (\(\sim 25\)Å plate separation) almost 90% of the anions are rejected.

which is completely in line with the observation of Muurinen et al. (1988) that “The effective porosity can even be less than one percent when the salt concentration is low and compaction high”, if only “effective porosity” is replaced by “concentration between the plates”.

It makes me a bit tired to discover that the record could have been set straight over 30 years ago regarding which pores anions can access. Instead the bentonite research community, for the most part, doubled down on the idea that anions only have accesses to parts of the pore volume, or that compacted bentonite contains a significant amount of bulk water.

An explicit description of interpreting “chloride through diffusion porosity” as a specific, limited part of the pore volume is given by Bradbury and Baeyens (2003)

In the interlayer spaces and regions where the individual montmorillonite stacks are in close proximity, double layer overlap will occur and anion exclusion effects will take place. Exclusion will probably be so large that it is highly unlikely that anions can move through these regions (Bolt and de Haan, 1982). However, Cl anions do move relatively readily through compacted bentonite since diffusion rates have been measured in ‘‘through-diffusion’’ tests […]

If the Cl anions cannot move through the interlayer and overlapping double layer regions because of anion exclusion effects, then it is reasonable to propose that the ‘‘free water’’ must provide the diffusion pathways (Fig. 1). Therefore, the hypothesis is that the pore volume associated with the transport of chloride (and other anions) is the ‘‘free water’’ volume, and that this is the porewater in a compacted bentonite.

Here they refer to Bolt and De Haan, (1982) 5, when arguing for that anions do not have access to interlayers. But the analysis in this reference is based on nothing but — the Poisson-Boltzmann equation! (which predicts anions everywhere)

Another thing to note is the notion of “overlapping” diffuse layers. Studies of negative adsorption to quantify surface area typically look at soil suspensions, with a solid part of a few percent. In such systems it is justified to perform the analysis on a single diffuse layer because the distance between separate montmorillonite particles is large enough. But at higher density there is not enough space between separate clay particles for the ion concentrations to ever reach the “external” value (\(c_0\)) — the diffuse layers “overlap”.6

It has been shown that effects of “overlapping” diffuse layers on the resulting negative adsorption is significant already at a a solid content of 6%. When carrying over the anion exclusion analysis to compacted bentonite — with solid content typically above 70%! — it therefore becomes near impossible to believe that the system should contain regions unaffected by the montmorillonite (“free water”). Yet, the argumentation above, apart from being flawed in the way it refers to the Poisson-Boltzmann equation, relies critically on the existence of such regions.

The mindful reader may remark that compacted bentonite, if it mainly contains “overlapping” diffuse layers, perhaps is devoid of anions after all. But the Poisson-Boltzmann equation predicts anions everywhere also for “overlapping” diffuse layers. Actually, the model by Soudek et al. (1984), discussed above, considers this case.

Despite the improbability that montmorillonite particles in compacted bentonite can be spaced so far apart as to allow for bulk water within the system, the idea of anions only having access to “free” water was nevertheless further pursued by Van Loon et al. (2007). They provide a picture similar to this

Stack in Van Loon et al. 2007

The idea here (and elsewhere) is that bentonite consists of “stacks” of individual montmorillonite particles (TOT-layers) interlaced with interlayer water.7 The space between “stacks” is assumed large enough for diffuse layers to fully develop, and to merge into a bulk solution (“free water”), whose volume depends on the ionic strength, reminiscent of the excluded volume in eq 1.8 Anions are postulated to only have access to this “free” water.

But as references for anion exclusion is once again simply given studies based on the Poisson-Boltzmann equation (in particular, Bolt and De Haan, (1982)). But these — as I hope has been made clear by now — predict anions everywhere, and consequently do not support the suggested model. In this case, the mismatch between model and supporting references stands out, as the term “effective porosity” is used interchangeably with the term “Cl-accessible porosity”; if Gouy-Chapman theory in a convoluted way can be used to define an “effective” porosity (having no other meaning than a fictitious, equivalent volume), there is no possibility whatsoever to use it to support the idea of anions having access to only parts of the pore space. Ironically, “anion-accessible porosity” seems to be the most popular term nowadays for describing effects of anion exclusion in compacted bentonite.

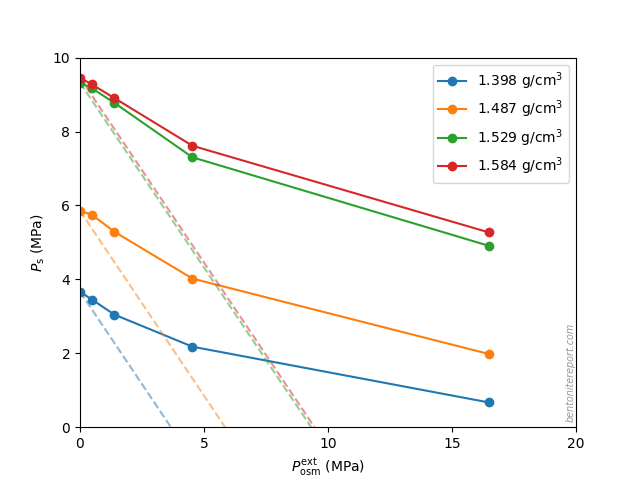
The strongest confirmation that the modern-day concept of anion-accessible porosity is simply a misuse of the exclusion-volume concept is given in Tournassat and Appelo (2011). They provide a quite extensive background for the type of anion exclusion they consider, and it is based on the excluded-volume concept discussed above. They even explicitly calculate the excluded-volume (named “total chloride exclusion distance”) only to directly discard it as not suitable

However, this binary representation (absence or presence of chloride, Fig. 3) is not very representative of the system since the EDL is not completely devoid of anions.

Yet, after making this statement that anions are everywhere (in the diffuse layer) they anyway define anion accessible porosity as an effective, fictitious volume!9

Interlayers

Apart from treating the diffuse layer incorrectly, Bradbury and Baeyens (2003), Van Loon et al. (2007) and Tournassat and Appelo (2011) all make the additional unjustified assumption that interlayers — which in these studies are defined as distinctly different from diffuse layers10 — are completely devoid of anions. Bradbury and Bans (2003) cites conventional Poisson-Boltzmann based studies to incorrectly support this claim (see above). Also Van Loon et al. (2007) use Bolt and De Haan, (1982) as a reference11

Due to the very narrow space, the double layers in the interlayers overlap and the electric potential in the truncated layer becomes large leading to a complete exclusion of anions from the interlayer (Bolt and de Haan, 1982; Pusch et al., 1990; Olin, 1994; Wersin et al., 2004). The interlayer water thus contains exclusively cations that compensate the permanent charges located in the octahedral layer of the clay.

Of the other sources cited, Pusch et al. (1990) mention “Donnan exclusion” as the reason preventing anions from having access to interlayers. But this is incorrect – Donnan equilibrium always gives a non-zero anion concentration in the interlayer (as long as the external concentration is non-zero). Wersin et al. (2004) only claim that anions are “excluded” from interlayers, without further explanation or references. (I haven’t managed to read Olin (1994) .)

Tournassat and Appelo (2011) cites Bourg et al. (2003) to support the claim that anions have no access to interlayers

When the dry density is above \(1.8 \;\mathrm{kg/dm^3}\), almost all the porosity resides in the interlayers of Na-montmorillonite. Since anions are excluded from the interlayers, the anion-accessible porosity becomes zero, and anion-diffusion is minimal (Bourg et al., 2003)

But in Bourg et al. (2003) is explicitly stated that anion exclusion from interlayers is only “partial”!

To sum up…

The idea that anions have access only to parts of the pore volume is widespread in today’s compacted bentonite research community. In this blog post I have shown that this idea emerges from misusing the concept of exclusion-volume, and that all references used to support ideas of “complete exclusion” rests on the Poisson-Boltzmann equation. The Poisson-Boltzmann equation, however, predicts anions everywhere! Thus, the concept of an anion-accessible porosity, and the related idea that compacted bentonite contains different “types” of water, have not been provided with any kind of theoretical support.

In contrast, the result that anions have access to the entire pore volume is further supported both by molecular dynamics simulations, as well as by the empirical evidence for salt in interlayers.

Footnotes

[1] This figure is just an illustration, not an actual result. Update (220831): Actual solutions to the Poisson-Boltzmann equation are presented here.

[2] Schofield writes with an enthusiasm seldom seen in modern scientific papers: “I considered that it would be possible to compute the negative adsorption of the repelled ions from the basic assumptions of Gouy’s theory of the diffuse electric double layer, and therefore invited Mr. M. H. Quenouille to tackle the mathematical difficulties involved. Complete solutions have now been obtained for electrolytes in which the ions have valency ratios 1:2, 1:1, and 2:1, and a full account of this work will be submitted for publication shortly.”

[3] “Bentonite” is used in the following as an abbreviation of “Bentonite and claystone”.

[4] I mean that the word “probably” as used here does not belong in a scientific text.

[5] Sciencedirect.com dates this reference to 1979. The book has a second revised edition, however, published in 1982.

[6] I use quotation marks when writing “overlap” because I think this wording gives the wrong impression in compacted clay: with an average distance between montmorillonite particles of around 1 nm, the concept of individual diffuse layers has lost its meaning.

[7] I plan to comment on “stacks” in a future blog post. Update (211027): Stacks make no sense.

[8] The volume is, however, not proportional to the Debye length, but depends exponentially on ionic strength.

[9] The “anion accessible porosity” is defined in this paper as \(\epsilon_{an} = \epsilon_{free} + \epsilon_D\cdot c_D/c_{free}\), where \(\epsilon_{free}\) is the porosity of a presumed bulk water phase in the bentonite, and \(\epsilon_D\) quantifies the volume of an arbitrarily chosen “Donnan volume” which is (Donnan) equilibrated with the “free” solution. \(c_D\) is the anion concentration in this “Donnan volume”, and \(c_{free}\) is the anion concentration in the bulk water.

[10] In this context, “interlayers” are defined as being parts of “stacks”. I really need to write about “stacks”… Update (211027): Stacks make no sense

[11] Bolt and de Haan (and others) are fond of writing that anions in very narrow confinement are “almost completely excluded” or “virtually completely excluded”, indicating that they may neglect anions in these compartments, but also that they are aware of that the equations they use never give exactly zero anion concentration. When working with soil suspensions of only a few percent solids it may be a valid approximation to neglect anions in nm-wide pores. In compacted bentonite it is not.

What is a “diffusion path” anyway?

Leave a reply

In a previous post I discussed how parts of the bentonite1 research community unjustifiably explain variation in (effective) diffusion rates as changes in “diffusion paths”. But what do authors really mean when using the term “diffusion path”?

In the geochemical/reactive transport literature, “diffusive pathways” are usually introduced when discussing the (presumably) related concept of tortuosity. For example, Steefel and Maher (2009) present a figure very similar to the one below, with the caption “Tortuous diffusion paths in porous material.”

Tortuous diffusion paths in porous material (Steefel and Maher (2009))

The text explains further that these are paths “the solute […] follow[s] in tortuous media”2. Several questions immediately arise. For example:

  • What is it, exactly, that follows these paths?
  • Why do the paths have a direction?
  • Why are these particular paths singled out? What stops e.g. the “Long Path” from taking this obvious shortcut:
Alternative path in Steefel and Maher's illustration

Let’s start with a hopefully obvious statement: Individual molecules or ions do not follow “paths” in a diffusive process, but conduct random motion. So paths as those in the figure above are certainly not trajectories of single particles.3

An answer to what is illustrated may be found in Van Brakel and Heertjes (1974) — a main reference in the bentonite research community when discussing tortuosity etc.4 In this work, the system is analyzed in steady-state, and the following description is given for “diffusion paths”

Assume the pore space of the porous medium to be completely filled with what we will call diffusion paths. The main direction of the diffusion paths is the same as that of the concentration gradient. In the way the diffusion paths wind through the pore space they can be compared with the streamlines for laminar flow in porous media.

Here it may sound as if the authors reject Fickian diffusion (which is always parallel to the concentration gradient), but it is rather that they use the term “concentration gradient” for denoting the externally applied constant concentration difference, required to maintain a steady-state flux. To me, this is quite confusing, because the comparison of diffusion paths with streamlines implies that they are directed along a (negative) concentration gradient. Two “gradients” must thus be kept in mind simultaneously: the external concentration difference, and the actual gradient on the pore-scale.

But with this distinction made, it is clear what Van Brakel and Heertjes mean by “diffusion paths”, and that their aim is to reduce a more complex 3D problem to an effective 1D description. It also becomes relatively clear that this is the way the term is used in much of the bentonite literature. It explains e.g. why the “paths” in the above picture (and others) have a direction: they must be thought of as the steady-state flow on the pore scale, with an implied constant concentration difference applied across the sample, making the macroscopic flow effectively 1D.

This implied reduction to steady-state transport in 1D is often found in the literature, e.g. in Shackelford and Moore (2013)

This increased tortuosity reduces the macroscopic concentration gradient (i.e., increases the distance over which the concentration difference is applied) and, therefore, reduces the diffusive mass flux relative to that which would exist in the absence of the porous medium.

or in Altman et al. (2015)

\(\tau\) is a geometrical factor (\(\le 1\)) representing the reduction in the effective concentration gradient (d(Me)/dx) due to the fact that diffusion paths through a porous medium will generally be greater, i.e. more tortuous, than the straight-line distance between the system boundaries, i.e. dx.

I am quite puzzled by this description for several reasons. Firstly, I find it unsatisfying that these definitions require the system to be in steady-state. Information on the influence of geometry is of course contained in the diffusion coefficient itself, independent of any external concentration differences. To associate “tortuosity” with such concentration differences, rather than with the mobility of the diffusing substance, seems inadequate to me. Moreover, the procedure of reducing a “macroscopic” concentration gradient due to path length seems to only work for an isolated path. At least, the procedure must become more involved for a system of connected paths, something I’ve not seen commented on by authors adopting this concept.

Secondly, note that a “diffusion path” — with the steady-state definition — simply indicates net mass transfer of diffusing substance. The absence of a “diffusion path” in a region does not mean that dissolved constituents don’t migrate there, but only that flux contributions in different directions add up to zero net mass transfer. I did a silly random walk simulation to illustrate this point (the concentration of walkers is kept at a constant finite value on the left side of the domain, while it is kept at zero on the right side)

Silly random walk

Note that with the definitions here discussed, we must accept that the vertical section in this illustration is not a diffusion path. This situation is quite distinct from laminar advective transport, where — if I’m thinking correctly — the absence of a streamline implies the absence of motion.

Thirdly, if you consider a porous system to be a network of thin cylinders, I guess the steady-state flux will basically resemble the the system itself (interconnected 1D-spaghetti configured in 3D). I suspect that this is the view many authors have in mind when speaking of “diffusion paths”. But, if so, why not simply speak of “paths”? Note also that the pore volume of smectitic systems mainly consists of 2D water films configured in 3D (it is lasagna, not spaghetti).

Lastly, what about non-steady-state transport? Concepts like the ones discussed here are also used when describing closed-cell diffusion tests , but are seldom (never?) defined in any other way. How could e.g. “tortuosity” reduce a macroscopically applied (1D) gradient in this case? And what is even meant by “diffusion paths”, if these are defined in steady-state? Since non-steady state is the general case, it would be more satisfying if quantities obtained under such circumstances were applied to the steady-state, rather than the other way around.

To get a feel for how pore geometry influences diffusion in non-steady-state, I conducted some more random walk simulations. In the animation below is compared random walks in an unrestricted 2D plane (blue) with random walks on a square net (red; strip width: 1 length unit, square size: 20 length units)

Random walks in 2D and on net

To quantify the diffusivity, we plot the average of the square of the displacements, \(\langle r^2 \rangle\), as a function of time5 in the two systems

<r2> vs t for 2D and isotropic net

We see that the diffusivity — which is directly proportional to the slope of these curves — is very close to twice as large in the unrestricted case as compared with diffusion on the net. From such a result it may be tempting to conclude that this reduction by a factor of two is due to longer “diffusion paths” on the net (and relate it to \(\sqrt{2}\), which conveniently is the ratio between the side and the diagonal of a square). But note that the diffusional process is isotropic also on the net, as demonstrated by identical slopes of the angle-resolved \(\langle r^2 \rangle\)-curves. Thus, interpreted in terms of “diffusion paths” on the net — however these should be defined — the conclusion is that the “paths” have the same length in any direction.

But the situation is easily analyzed from the simple model underlying the figures displayed above: in the 2D-plane, the random walk process has a maximized variance, because movements in the \(x-\) and \(y-\)directions are uncorrelated. The net geometry, on the other hand, correlates these variables: if a walker has free passage in the \(y\)-direction, it is restricted in the \(x\)-direction, and vice versa. Thus, the diffusivity is not diminished due to longer “paths”, but because the geometrical restrictions reduce the variance of the underlying process. This effect will depend on the relative reduction of dimensions: with line-like pores in a 3D configuration, the reduction factor becomes 1/3 (I guess this is what what is alluded to for a “homogeneous isotropic pore network” in the often-cited work Dykhuzien and Casey (1989) ), but for the case relevant for bentonite — diffusion in 2D-planes configured in 3D — the factor is 2/3 (which I haven’t seen stated anywhere). I furthermore don’t understand why such a factor should be termed “tortuosity”, because there is nothing intrinsically “tortuous” about it (in a sense one could even argue that individual trajectories in the unrestricted 2D-plane are more “tortuous” than the ones on the net).

By making the net non-isotropic, e.g. by replacing the squares by rectangles like this

Rectangluar net

the correlation between the \(x\)- and \(y\)-variables alters (it is now twice as likely for a walker to have no restriction in the \(y\)-direction as in the \(x\)-direction), which is directly reflected in the diffusivities

<r2> vs t for square and rectangular net

The diffusivity in the \(y\)-direction is now about twice as large as the diffusivity in the \(x\)-direction. Also the diffusivity in the diagonal directions is significantly larger than in the \(x\)-direction. Following a naive definition of “tortuosity”, this result may seem surprising (is the “solute” in the \(x\)-direction following a longer path than than in the diagonal directions?). Still, with a correct averaging procedure I guess the diffusivity can be related to “paths” on the net (However, I still don’t understand how to differ “diffusion paths” from geometrical paths).

With these simulations I simply want to argue for that it seems considerably more subtle and complex to relate pore geometry to diffusivity, than how it typically is presented in the bentonite literature. To be frank, I consider most talk about “diffusion paths” in the bentonite literature, as well as most definitions of various geometric factors, to be just that: talk. There is an established “tradition” to mention certain concepts (geometric factors, tortuosity, constrictivity, paths…), but in the end the introduced factors are usually only functioning as fudge factors, leading to unjustified claims about the nature of bentonite. Similarly, discussions on actual values of such factors are in principle always only qualitative.

As an example, Choi and Oscarson (1996) interpret different values of diffusivity measured in Na- and Ca-bentonite directly as a difference in “tortuosity”:

We attribute this to the larger quasicrystal, or particle, size of Ca- compared to Na-bentonite. Hence, Ca-bentonite has a greater proportion of relatively large pores; this was confirmed by Hg intrusion porosimetry. This means the diffusion pathways in Ca-bentonite are less tortuous than those in Na-bentonite.

But they could have been considerably more quantitative than this. In the paper, tortuosity is defined as \(\tau = L^2/L_e^2\), where “\(L\) is the straight-line macroscopic distance between two points defining the transport path, and \(L_e\) is the actual, microscopic or effective distance between the same two points.” Tortuosity is furthermore evaluated from HTO diffusion to \(\tau_{\ce{Na}} = 0.062\) in Na-bentonite, and \(\tau_{\ce{Ca}} = 0.117\) in Ca-bentonite. Combining these expressions gives \(L_{e,\ce{Na}} = 1.37\cdot L_{e,\ce{Ca}}\).

What is implicitly said in this work is thus that the “actual, microscopic or effective distance between two points” is 1.37 times longer in Na-bentonite as compared with Ca-bentonite. I mean that it would be suitable for authors making these kind of (implicit) claims to provide a quantitative idea of how the pore space is modified in order to achieve this particular alteration of distances. To me, it is not even obvious why “larger quasicrystals” implies shorter “diffusion paths” — note that the effect of the “net” geometries above are scale independent.

But rather than making a quantitative discussion, Choi and Oscarson (1996) give the following caveat

In reality, \(\tau\) may account for more than just the pore geometry of the clay. Another factor that may be included in \(\tau\) is, for instance, the variation in the viscosity of the solution within the pore space (Kemper et al., 1964).

I find this an incredible statement. It is similar to saying that, “in reality”, Earth’s gravity constant (\(g\)) may include effects of air resistance.

Footnotes

[1] “Bentonite” is used in the following as an abbreviation of “Bentonite and claystone”.

[2] That is at least my interpretation. A fuller quotation reads: “[Tortuosity] is defined as the ratio of the path length the solute would follow in water alone, \(L\), relative to the tortuous path length it would follow in porous media, \(L_e\)” (while the following equation actually contains the square of this ratio).

[3] I am not fully convinced that all authors keep this in mind at all times. How should e.g. the following passage from Charlet et al. (2017) be interpreted: “An important geometric parameter is the tortuosity factor, \(\tau\), that quantifies the travelled distance of a dissolved constituent through the pore network compared to actual distance between two points.”? Or this one from Van loon et al. (2018) : “The tortuosity is a measure for path lengthening and takes into account that molecules have to diffuse around grains and thus take a longer way.”?

[4] Which is quite amazing, considering that this paper deals with diffusion in a gas phase in macroporous systems.

[5] Since all walkers start in the same point (the origin) the data show finite-size effects for small times. The presented data is therefore taken after an initiation time, labeled \(t^\star\).

Evidence for anions in montmorillonite interlayers (swelling pressure, part II)

2 Replies

It is easy to find models assuming montmorillonite interlayers devoid of “anions” . Here I will present empirical evidence that such an assumption is incorrect. Before doing so, just a quick remark on the term “anions” in this context. If anions reside in interlayers, they certainly do so accompanied by excess cations, in order to maintain overall charge neutrality. Thus, when speaking of “anions” in the interlayer we really mean “salt” (= anion(s) + cation(s)). In the following I will use the term “salt” because it better reflects the overall charge neutral character of the process (we are not interested in pushing a handful of negative charge into an interlayer).

The nature of bentonite swelling

The evidence for salt having access to interlayers follows directly from the observed swelling pressure response to changes in external salinity. It is therefore important to first understand the thermodynamic basis for swelling pressure, which I wrote about in an earlier post (the same nomenclature is adopted here). In essence, swelling is a consequence of balancing the water chemical potential1 in the clay with that in the external solution2, and swelling pressure quantifies the difference in chemical potential between the external solution and the non-pressurized bentonite sample, as illustrated here

chemical potentials in non-pressurizied bentoniote and in external solution

Since the chemical potential in the external solution depends on the salt content, we generally expect a response in swelling pressure when altering external salinity.

Labeling the salt concentration \(c^{ext}\), we write the chemical potential of the external solution in terms of an osmotic pressure3

\begin{equation}
\mu_w^{ext} = \mu_0 – P_{osm.}^{ext}(c^{ext})\cdot v_w
\tag{1}
\end{equation}

where \(v_w\) is the partial molar volume of water. \(P_{osm}^{ext}\) is not the pressure in the external solution, but the pressure that would be required to keep the solution in equilibrium with pure water. The actual pressure in this compartment is the same as for the reference state: \(P_0\). It may seem confusing to use a “pressure” to specify the chemical potential, but we will see that it has its benefits. Experimentally we have full control of \(P_{osm}^{ext}\) by choosing an appropriate \(c^{ext}\).

Response in an indifferent clay

With salt in the external solution, the big question is what happens to the chemical potential of the clay. We will start by assuming (incorrectly) that external salt cannot access the interlayers. This means that the chemical potential of the (non-pressurized) bentonite does not change when the external salinity changes. We refer to this hypothetical bentonite as indifferent. In analogy with the external solution, we write the chemical potential of the indifferent non-pressurized bentonite as4 \begin{equation} \mu_w^{int}(P_0) = \mu_0 -P_s^0\cdot v_w \;\; \;\; \;\; \text{(indifferent clay)} \end{equation}

were \(P_s^0\) is the swelling pressure in case of pure water as external solution. By assumption, \(\mu_w^{int}(P_0)\) does not depend on the external salinity (it is independent of \(P_{osm}^{ext}\)). The chemical potential in the indifferent clay at an elevated pressure \(P\) is

\begin{equation}
\mu_w^{int}(P) = \mu_0 – P_s^0\cdot v_w +(P-P_0)\cdot v_w \;\;
\;\; \;\; \text{(indifferent clay)}
\tag{2}
\end{equation}

The swelling pressure (defined as the difference in pressure between bentonite and external solution, when the two are in equilibrium: \(P_s \equiv P_{eq} – P_0\)) in an indifferent clay is given by equating eqs. 1 and 2, giving the neat formula

\begin{equation}
P_s(c^{ext}) = P_s^0 – P_{osm}^{ext}(c^{ext}) \;\; \;\; \;\;
\text{(indifferent clay)}
\end{equation}

Note the following:

  • Although an indifferent clay is not affected by salt, it certainly has a swelling pressure response, demonstrating that swelling pressure depends as much on the external solution as it does on the clay.
  • Since swelling pressure in this case decreases linearly with the osmotic pressure of the external solution, it is predicted to vanish when the osmotic pressure equals \(P_s^0\).
  • External osmotic pressures larger than \(P_s^0\) implies “drying” of the clay (water transport from the clay into the external compartment)

If the above derivation feels a bit messy, with all the different types of pressure quantities to keep track of, here is a hopefully helpful animation

Animation swelling pressure response without anions in interlayer

Real swelling pressure response

Equipped with the swelling pressure response of an indifferent clay, let’s compare with the real response: The swelling pressure response in real bentonite deviates strongly from the indifferent clay response. This is seen e.g. here for Na-montmorillonite equilibrated in sequence with NaCl solutions of increasing concentration5 (data from Karnland et al., 2005 )

Swelling pressure response to salinities mid range densities

Swelling pressure indeed drops with increased concentration, but the drop is not linear in \(P^{ext}_{osm}\), and is weaker as compared with the indifferent clay response (shown by dashed lines). All samples in the diagram above exert swelling pressure when \(P^{ext}_{osm} \gg P_s^0\), i.e. far beyond the point where the swelling pressure in an indifferent clay is lost.

The deviation of the observed response from that of an indifferent clay directly demonstrates that the clay is affected by salt, i.e. that the chemical potential of the non-pressurized clay depends on the external salt concentration. The only reasonable way for salt to influence the chemical potential in the bentonite is of course to reside in the interlayer pores. Consequently, the observed swelling pressure response proves that salt from the external solution enters the interlayer pores.

Here is an illustration of how the chemical potentials relate to the swelling pressure in real bentonite

Swelling pressure repsonse real bentonite

Although the observed swelling pressure response in itself is sufficient to dismiss the idea that salt does not have access to interlayers, the study by Karnland et al., (2005) provides a much broader verification of the thermodynamic nature of swelling pressure. In particular, the chemical potential was measured (by means of vapor pressure) separately in the same samples as used for swelling pressure tests, after they had been isolated and unloaded. The terms in the relation \(P_s = \left(\mu_w^{ext} – \mu_w^{int}(P_0) \right)/v_w\) were thus checked independently, as indicated here

Measurements performed in Karnland et al. (2005)

A striking confirmation of salt residing in interlayers is given by the observation that the chemical potential in the non-pressurized samples is lower than that in the corresponding external solution, as well as that in non-pressurized samples of similar density, but equilibrated with pure water.

Another interesting observation is that the sample with the highest density behaves qualitatively similar to the others: although the external osmotic pressure never exceeded \(P_s^0\) (\(\approx\)56 MPa), the response strongly deviates from that of an indifferent clay

swelling pressure response to salinity high density

Because the pore space of samples this dense (\(2.02\;\mathrm{g/cm^3}\)) mainly consists of mono- and bihydrated interlayers, this similarity in response shows that salt has access also to such pores.

Implications

The issue of whether “anions” have access to montmorillonite interlayers has — for some reason — been a “hot” topic within the bentonite research community for a long time, and a majority of contemporary models rest on some version of the assumption that “anions” does not have access to the full pore volume. But, as far as I can see, this whole idea is based on misconceptions. I guess that saying so may sound quite grandiose, but note that swelling pressure is not at all considered in most chemical models of bentonite. And if it is, it is usually treated incorrectly. As an example, here is what Bradbury and Baeyens (2003) writes in a very influential publication

One of the main premises in the approach proposed here is that highly compacted bentonite can function as an efficient semi-permeable membrane (Horseman et al., 1996). This implies that the re-saturation of compacted bentonite involves predominantly the movement of water molecules and not solute molecules. Thus, to a first approximation, the composition of the external saturating aqueous phase should be a second-order effect which has little influence on the initial compacted bentonite porewater composition.

If the composition of the re-saturating water were to play an important role in determining the porewater composition, then it should also have a significant influence on swelling (Bolt, 1979). Dixon (2000) recently reviewed the role of salinity on the development of swelling pressure in bentonite buffer and backfill materials. He concluded that provided the initial dry densities were greater than 900 \(\mathrm{kg\;m^{-3}}\), the swelling pressures developed are unaffected for groundwater salinities \(< 75 \;\mathrm{g\;l^{-1}}\). Even brines appear to have little or no influence for initial dry densities \(>1500 \;\mathrm{kg\;m^{-3}}\).

But, as we just have learned, a system with a weak swelling pressure response necessarily has a significant contribution to its water chemical potential due to externally provided salt. In contrast, the approximation discussed in the first paragraph of the quotation — which is basically that of an indifferent clay — maximizes the swelling pressure response. Thus, the discussed “main premise” does not hold, and the provided empirical “support” is actually an argument for the opposite (i.e. that salt has access to the clay).

Footnotes

[1] In the following I will write only “chemical potential” — it is always the chemical potential of water that is referred to.

[2] This is just a complicated way of saying that swelling is (an effect of) osmosis.

[3] Some may say that \(P_{osm}^{ext}\) is simply the “suction” of the solution, but I am not a fan of using that concept in this context. I will comment on “suction” in a later blog post.

[4] The density dependence of the chemical potential in the bentonite is not explicitly stated here, in order to keep the formulas readable, but we assume throughout that the bentonite has some specific water-to-solid mass ratio \(w\).

[5] The NaCl concentrations are 0.0 M, 0.1 M, 0.3 M, 1.0 M, and 3.0 M.